324 results in 60Hxx
Perpetuities with thin tails
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 463-480
- Print publication:
- June 1996
-
- Article
- Export citation
Dispersion of particle systems in Brownian flows
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 53-74
- Print publication:
- March 1996
-
- Article
- Export citation
Lundberg inequalities for a Cox model with a piecewise constant intensity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 196-210
- Print publication:
- March 1996
-
- Article
- Export citation
Bisexual branching diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 980-1018
- Print publication:
- December 1995
-
- Article
- Export citation
Stochastic vector difference equations with stationary coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 851-866
- Print publication:
- December 1995
-
- Article
- Export citation
General necessary conditions for partially observed optimal stochastic controls
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1118-1137
- Print publication:
- December 1995
-
- Article
- Export citation
Persistence of a critical super-2 process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 534-540
- Print publication:
- June 1995
-
- Article
- Export citation
Randomly perturbed vibrations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 417-428
- Print publication:
- June 1995
-
- Article
- Export citation
Pricing via anticipative stochastic calculus
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1006-1021
- Print publication:
- December 1994
-
- Article
- Export citation
Approximations and boundary conditions for continuous-time threshold autoregressive processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1103-1109
- Print publication:
- December 1994
-
- Article
- Export citation
On maintained systems operating in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 589-594
- Print publication:
- June 1994
-
- Article
- Export citation
Stochastic models of environmental pollution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 377-403
- Print publication:
- June 1994
-
- Article
- Export citation
On the solution of Kac-type partial differential equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 311-324
- Print publication:
- 1994
-
- Article
- Export citation
Burgers' equation by non-local shot noise data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 351-362
- Print publication:
- 1994
-
- Article
- Export citation
Limiting behaviour of two-level measure-branching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 773-782
- Print publication:
- December 1993
-
- Article
- Export citation
Stochastic non-linear oscillators
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 649-666
- Print publication:
- September 1993
-
- Article
- Export citation
A martingale approach to the PASTA property
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 252-257
- Print publication:
- March 1993
-
- Article
- Export citation
An extension of the Cameron–Martin result
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 247-251
- Print publication:
- March 1993
-
- Article
- Export citation
Asymptotic variance parameters for the boundary local times of reflected Brownian motion on a compact interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 996-1002
- Print publication:
- December 1992
-
- Article
- Export citation
Concavity and reflected Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 209-215
- Print publication:
- March 1992
-
- Article
- Export citation

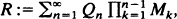 where
where 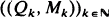 is an independent, identically distributed sequence with
is an independent, identically distributed sequence with 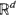 Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as
Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as 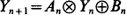 based on various choices of binary operations
based on various choices of binary operations 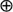 and
and 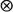 , assuming that
, assuming that 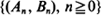 are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is
are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is 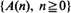 . Under this and mild additional conditions, the process
. Under this and mild additional conditions, the process 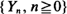 has a unique finite stationary distribution to which it converges from all initial conditions.
has a unique finite stationary distribution to which it converges from all initial conditions.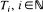
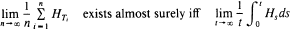
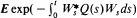 where
where 
