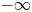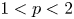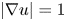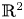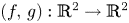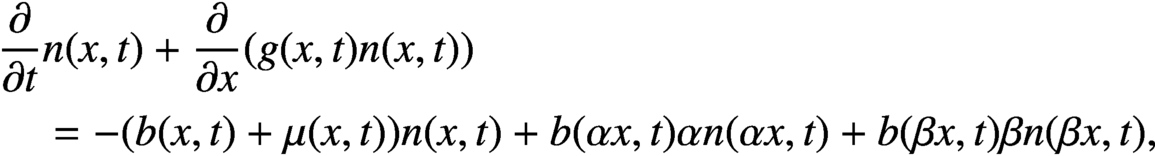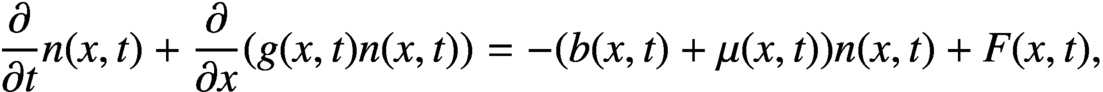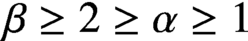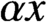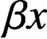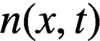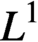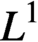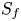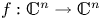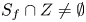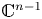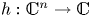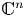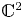23 results in 35Fxx
Time almost periodicity for solutions of Toda lattice equation with almost periodic initial datum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-40
-
- Article
- Export citation
Models for information propagation on graphs
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OPTIMAL QUEUING STRATEGIES FOR AN M/G/1 RETRIAL QUEUE SYSTEM WITH RWV AND ISEV POLICIES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 19 March 2024, pp. 384-410
-
- Article
-
- You have access
- HTML
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1313-1335
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
On Lebesgue points of entropy solutions to the eikonal equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 23 May 2023, pp. 1047-1059
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Modelling, simulation and optimisation of parabolic trough power plants
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 592-615
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FOURIER-TYPE CHARACTERISATION FOR GEVREY VECTORS ON HYPO-ANALYTIC STRUCTURES AND PROPAGATION OF GEVREY SINGULARITIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 07 February 2022, pp. 2177-2198
- Print publication:
- September 2023
-
- Article
- Export citation
A weight-homogenous condition to the real Jacobian conjecture in $ {\mathbb {R}}^{2}$
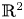
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 19 November 2021, pp. 1028-1036
-
- Article
- Export citation
Invasion fronts and adaptive dynamics in a model for the growth of cell populations with heterogeneous mobility
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 766-783
-
- Article
- Export citation
ESTIMATES FOR APPROXIMATE SOLUTIONS TO A FUNCTIONAL DIFFERENTIAL EQUATION MODEL OF CELL DIVISION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 12 March 2021, pp. 469-488
-
- Article
- Export citation
Envelopes of families of framed surfaces and singular solutions of first-order partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1515-1542
- Print publication:
- October 2021
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
Entire solutions of a variation of the eikonal equation and related PDEs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 697-708
-
- Article
- Export citation
Analysis of an age-structured HIV in-host model with proliferation and two infection modes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 806-827
-
- Article
- Export citation
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
MICROLOCAL REGULARITY FOR MIZOHATA TYPE DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1185-1209
- Print publication:
- July 2020
-
- Article
- Export citation
Solving the Equation
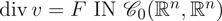 $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
$\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1055-1061
-
- Article
- Export citation
Optimal stability estimates for continuity equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 16 July 2018, pp. 1279-1296
- Print publication:
- December 2018
-
- Article
- Export citation
ON A CELL DIVISION EQUATION WITH A LINEAR GROWTH RATE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 3 / January 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 293-312
-
- Article
-
- You have access
- Export citation
Flows of measures generated by vector fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 773-818
- Print publication:
- August 2018
-
- Article
- Export citation