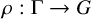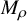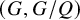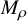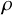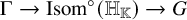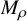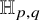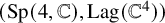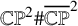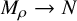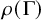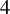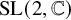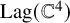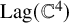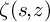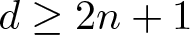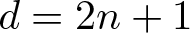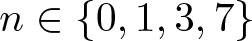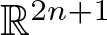150 results in 57Rxx
Periodic points of rational area-preserving homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fiber bundles associated with Anosov representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SU(2)-bundles over highly connected 8-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1-30
-
- Article
- Export citation
Graphing, homotopy groups of spheres, and spaces of long links and knots
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free torus actions and twisted suspensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Floer homology and non-fibered knot detection
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New classes of quasigeodesic Anosov flows in
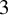 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The homology of moduli spaces of 4-manifolds may be infinitely generated
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant covering type and the number of vertices in equivariant triangulations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Principal bundle structure of the space of metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation
PL homeomorphisms of surfaces and codimension 2 PL foliations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2684-2703
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REIDEMEISTER’S THEOREM USING TRANSVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 356-367
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
ZETA INVARIANTS OF MORSE FORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 411-480
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin links and Conway spheres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1467-1524
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The homotopy decomposition of the suspension of a non-simply-connected five-manifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
Global index of real polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
Unit sphere fibrations in Euclidean space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 287-298
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum: A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 729-730
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Chern classes in equivariant bordism
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation