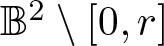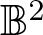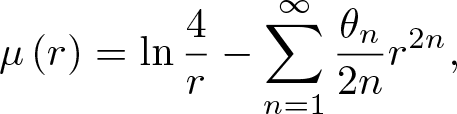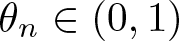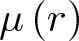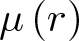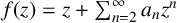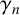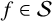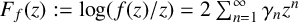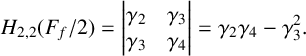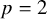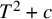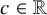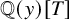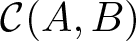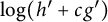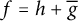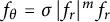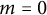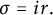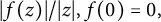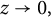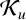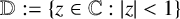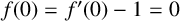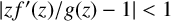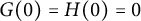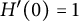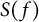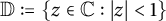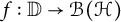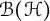156 results in 30Cxx
VARIABILITY REGIONS FOR THE nth DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-11
-
- Article
- Export citation
On boundary-non-preserving mappings with Poletsky inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-22
-
- Article
- Export citation
Schwarz lemma for harmonic functions in the unit ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-18
-
- Article
- Export citation
UPPER BOUNDS ON POLYNOMIAL ROOT SEPARATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finely quasiconformal mappings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
Series expansion, higher-order monotonicity properties and inequalities for the modulus of the Grötzsch ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 16-43
-
- Article
-
- You have access
- HTML
- Export citation
Second Hankel determinant of logarithmic coefficients of inverse strongly starlike functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 1196-1211
-
- Article
-
- You have access
- HTML
- Export citation
THE SHARP BOUND OF THE SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS FOR STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
On Harnack inequality and harmonic Schwarz lemma
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 940-954
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SECOND HANKEL DETERMINANT FOR LOGARITHMIC INVERSE COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 128-139
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Schwarzian norm estimates for Janowski convex functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 299-315
-
- Article
-
- You have access
- HTML
- Export citation
Integral mean estimates for univalent and locally univalent harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 655-669
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Nonlinear Beltrami equation: lower estimates of Schwarz lemma’s type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 533-543
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Normal families and quasiregular mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 79-112
-
- Article
-
- You have access
- HTML
- Export citation
HARMONIC-MEASURE DISTRIBUTION FUNCTIONS AND RELATED FUNCTIONS FOR SIMPLY CONNECTED AND MULTIPLY CONNECTED TWO-DIMENSIONAL REGIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 163-164
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 365-375
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Landau-type theorems for certain bounded bi-analytic functions and biharmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 152-165
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr operator on operator-valued polyanalytic functions on simply connected domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1411-1422
- Print publication:
- December 2023
-
- Article
- Export citation