Book contents
- Frontmatter
- Dedication
- Preface
- Contents
- I Limits and Differentiation
- II Integration
- 16 Combinatorial identities for Riemann sums
- 17 Summation by parts
- 18 Integration by parts
- 19 The world's sneakiest substitution
- 20 Symmetry and integration
- 21 Napier's inequality and the limit for e
- 22 The nth root of n! and another limit for e
- 23 Does shell volume equal disk volume?
- 24 Solids of revolution and the Cauchy-Schwarz inequality
- 25 The midpoint rule is better than the trapezoidal rule
- 26 Can the midpoint rule be improved?
- 27 Why is Simpson's rule exact for cubics?
- 28 Approximating π with integration
- 29 The Hermite-Hadamard inequality
- 30 Polar area and Cartesian area
- 31 Polar area as a source of antiderivatives
- 32 The prismoidal formula
- III Infinite Series
- IV Additional Topics
- V Appendix: Some Precalculus Topics
- Solutions to the Exercises
- References
- Index
- About the Author
This chapter is part of a book that is no longer available to purchase from Cambridge Core
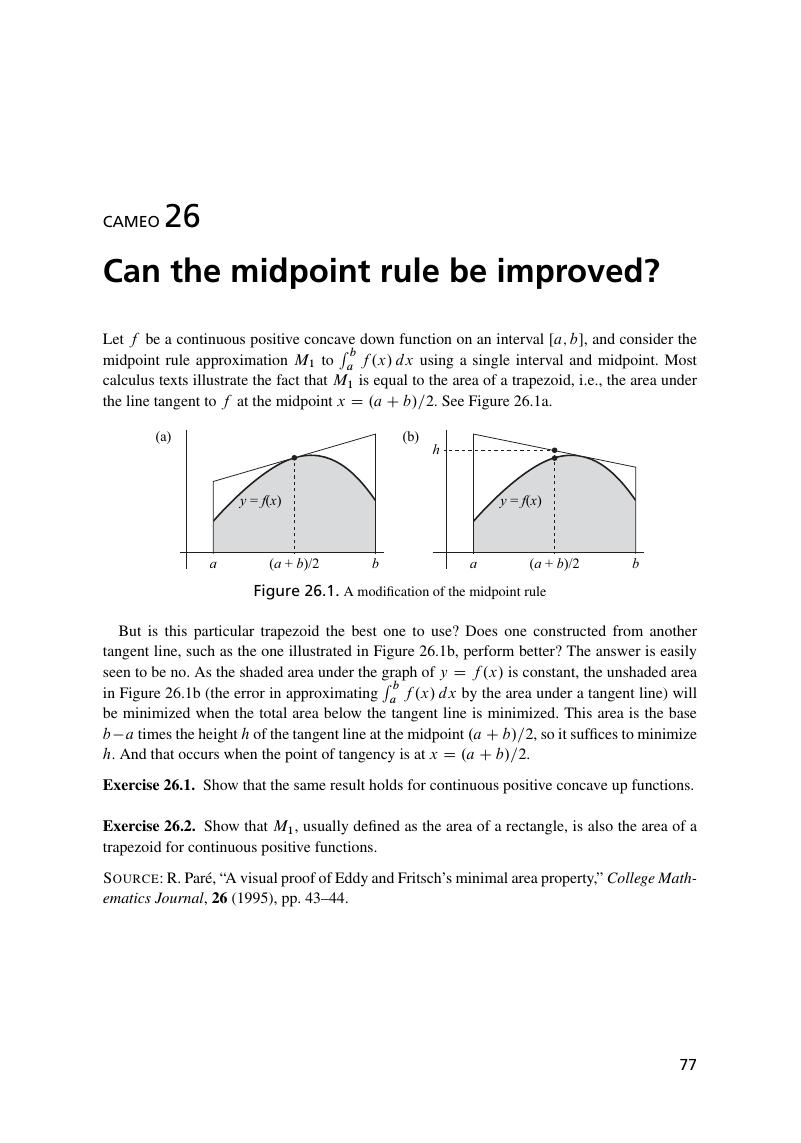
26 - Can the midpoint rule be improved?
from II - Integration
Book contents
- Frontmatter
- Dedication
- Preface
- Contents
- I Limits and Differentiation
- II Integration
- 16 Combinatorial identities for Riemann sums
- 17 Summation by parts
- 18 Integration by parts
- 19 The world's sneakiest substitution
- 20 Symmetry and integration
- 21 Napier's inequality and the limit for e
- 22 The nth root of n! and another limit for e
- 23 Does shell volume equal disk volume?
- 24 Solids of revolution and the Cauchy-Schwarz inequality
- 25 The midpoint rule is better than the trapezoidal rule
- 26 Can the midpoint rule be improved?
- 27 Why is Simpson's rule exact for cubics?
- 28 Approximating π with integration
- 29 The Hermite-Hadamard inequality
- 30 Polar area and Cartesian area
- 31 Polar area as a source of antiderivatives
- 32 The prismoidal formula
- III Infinite Series
- IV Additional Topics
- V Appendix: Some Precalculus Topics
- Solutions to the Exercises
- References
- Index
- About the Author
Summary
A summary is not available for this content so a preview has been provided. Please use the Get access link above for information on how to access this content.
- Type
- Chapter
- Information
- Cameos for CalculusVisualization in the First-Year Course, pp. 77 - 78Publisher: Mathematical Association of AmericaPrint publication year: 2015