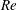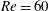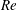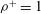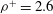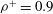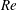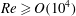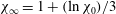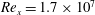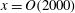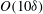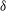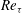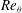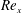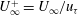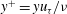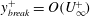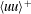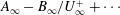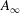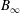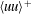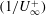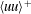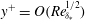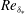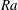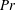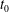Papers
On the late-time behaviour of a bounded, inviscid two-dimensional flow
-
- Published online by Cambridge University Press:
- 13 October 2015, pp. 1-22
-
- Article
- Export citation
Optimal dynamo action by steady flows confined to a cube
-
- Published online by Cambridge University Press:
- 13 October 2015, pp. 23-45
-
- Article
- Export citation
Conjugated liquid layers driven by the short-wavelength Bénard–Marangoni instability: experiment and numerical simulation
-
- Published online by Cambridge University Press:
- 13 October 2015, pp. 46-71
-
- Article
- Export citation
Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 14 October 2015, pp. 72-102
-
- Article
- Export citation
Three-dimensional effects on flag flapping dynamics
-
- Published online by Cambridge University Press:
- 19 October 2015, pp. 103-136
-
- Article
- Export citation
Microstructured optical fibre drawing with active channel pressurisation
-
- Published online by Cambridge University Press:
- 13 October 2015, pp. 137-165
-
- Article
- Export citation
Frequency–wavenumber mapping in turbulent shear flows
-
- Published online by Cambridge University Press:
- 15 October 2015, pp. 166-190
-
- Article
- Export citation
Density-ratio effects on the capture of suspended particles in aquatic systems
-
- Published online by Cambridge University Press:
- 15 October 2015, pp. 191-210
-
- Article
- Export citation
Waves in Newton’s bucket
-
- Published online by Cambridge University Press:
- 16 October 2015, pp. 211-250
-
- Article
- Export citation
Oscillatory superfluid Ekman pumping in helium II and neutron stars
-
- Published online by Cambridge University Press:
- 16 October 2015, pp. 251-282
-
- Article
- Export citation
Homoclinic snaking near the surface instability of a polarisable fluid
-
- Published online by Cambridge University Press:
- 16 October 2015, pp. 283-305
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wake-induced ‘slaloming’ response explains exquisite sensitivity of seal whisker-like sensors
-
- Published online by Cambridge University Press:
- 16 October 2015, pp. 306-322
-
- Article
- Export citation
A CFD-informed quasi-steady model of flapping-wing aerodynamics
-
- Published online by Cambridge University Press:
- 16 October 2015, pp. 323-343
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of non-circular finite-release gravity currents
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. 344-378
-
- Article
- Export citation
Evolution of zero-pressure-gradient boundary layers from different tripping conditions
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. 379-411
-
- Article
- Export citation
Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. 412-447
-
- Article
- Export citation
Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. 448-473
-
- Article
- Export citation
Large-Reynolds-number asymptotics of the streamwise normal stress in zero-pressure-gradient turbulent boundary layers
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. 474-503
-
- Article
- Export citation
On the contact-line pinning in cavity formation during solid–liquid impact
-
- Published online by Cambridge University Press:
- 26 October 2015, pp. 504-525
-
- Article
- Export citation
A novel heat transfer switch using the yield stress
-
- Published online by Cambridge University Press:
- 26 October 2015, pp. 526-566
-
- Article
- Export citation