Article contents
Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows
Published online by Cambridge University Press: 22 October 2015
Abstract
We consider the flow of a Newtonian fluid in a three-dimensional domain, rotating about a vertical axis and driven by a vertically invariant horizontal body force. This system admits vertically invariant solutions that satisfy the 2D Navier–Stokes equation. At high Reynolds number and without global rotation, such solutions are usually unstable to three-dimensional perturbations. By contrast, for strong enough global rotation, we prove rigorously that the 2D (and possibly turbulent) solutions are stable to vertically dependent perturbations. We first consider the 3D rotating Navier–Stokes equation linearized around a statistically steady 2D flow solution. We show that this base flow is linearly stable to vertically dependent perturbations when the global rotation is fast enough: under a Reynolds-number-dependent threshold value 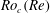 $Ro_{c}(Re)$ of the Rossby number, the flow becomes exactly 2D in the long-time limit, provided that the initial 3D perturbations are small. We call this property linear two-dimensionalization. We compute explicit lower bounds on
$Ro_{c}(Re)$ of the Rossby number, the flow becomes exactly 2D in the long-time limit, provided that the initial 3D perturbations are small. We call this property linear two-dimensionalization. We compute explicit lower bounds on 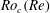 $Ro_{c}(Re)$ and therefore determine regions of the parameter space
$Ro_{c}(Re)$ and therefore determine regions of the parameter space 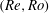 $(Re,Ro)$ where such exact two-dimensionalization takes place. We present similar results in terms of the forcing strength instead of the root-mean-square velocity: the global attractor of the 2D Navier–Stokes equation is linearly stable to vertically dependent perturbations when the forcing-based Rossby number
$(Re,Ro)$ where such exact two-dimensionalization takes place. We present similar results in terms of the forcing strength instead of the root-mean-square velocity: the global attractor of the 2D Navier–Stokes equation is linearly stable to vertically dependent perturbations when the forcing-based Rossby number 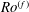 $Ro^{(f)}$ is lower than a Grashof-number-dependent threshold value
$Ro^{(f)}$ is lower than a Grashof-number-dependent threshold value 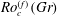 $Ro_{c}^{(f)}(Gr)$. We then consider the fully nonlinear 3D rotating Navier–Stokes equation and prove absolute two-dimensionalization: we show that, below some threshold value
$Ro_{c}^{(f)}(Gr)$. We then consider the fully nonlinear 3D rotating Navier–Stokes equation and prove absolute two-dimensionalization: we show that, below some threshold value 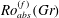 $Ro_{\mathit{abs}}^{(f)}(Gr)$ of the forcing-based Rossby number, the flow becomes two-dimensional in the long-time limit, regardless of the initial condition (including initial 3D perturbations of arbitrarily large amplitude). These results shed some light on several fundamental questions of rotating turbulence: for arbitrary Reynolds number
$Ro_{\mathit{abs}}^{(f)}(Gr)$ of the forcing-based Rossby number, the flow becomes two-dimensional in the long-time limit, regardless of the initial condition (including initial 3D perturbations of arbitrarily large amplitude). These results shed some light on several fundamental questions of rotating turbulence: for arbitrary Reynolds number 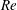 $Re$ and small enough Rossby number, the system is attracted towards purely 2D flow solutions, which display no energy dissipation anomaly and no cyclone–anticyclone asymmetry. Finally, these results challenge the applicability of wave turbulence theory to describe stationary rotating turbulence in bounded domains.
$Re$ and small enough Rossby number, the system is attracted towards purely 2D flow solutions, which display no energy dissipation anomaly and no cyclone–anticyclone asymmetry. Finally, these results challenge the applicability of wave turbulence theory to describe stationary rotating turbulence in bounded domains.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 44
- Cited by





