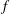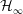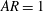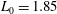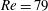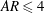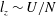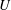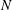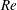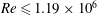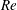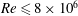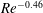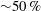JFM Rapids
Exact solutions of asymmetric baroclinic quasi-geostrophic dipoles with distributed potential vorticity
-
- Published online by Cambridge University Press:
- 12 April 2019, R1
-
- Article
- Export citation
A bulk-interface correspondence for equatorial waves
-
- Published online by Cambridge University Press:
- 10 April 2019, R2
-
- Article
- Export citation
On the robustness of emptying filling boxes to sudden changes in the wind
-
- Published online by Cambridge University Press:
- 11 April 2019, R3
-
- Article
- Export citation
Subharmonic edge wave excitation by narrow-band, random incident waves
-
- Published online by Cambridge University Press:
- 12 April 2019, R4
-
- Article
- Export citation
The instability of gyrotactically trapped cell layers
-
- Published online by Cambridge University Press:
- 15 April 2019, R5
-
- Article
- Export citation
Focus on Fluids
Thermal forcing and ‘classical’ and ‘ultimate’ regimes of Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 03 April 2019, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Shear-induced collective diffusivity down a concentration gradient in a viscous emulsion of drops
-
- Published online by Cambridge University Press:
- 03 April 2019, pp. 5-25
-
- Article
- Export citation
Linear iterative method for closed-loop control of quasiperiodic flows
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 26-65
-
- Article
- Export citation
Evolution of elliptic synthetic jets at low Reynolds number
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 66-96
-
- Article
- Export citation
Layer formation and relaminarisation in plane Couette flow with spanwise stratification
-
- Published online by Cambridge University Press:
- 10 April 2019, pp. 97-118
-
- Article
-
- You have access
- HTML
- Export citation
Viscous control of shallow elastic fracture: peeling without precursors
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 119-140
-
- Article
- Export citation
Viscous extension of potential-flow unsteady aerodynamics: the lift frequency response problem
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 141-175
-
- Article
- Export citation
High-speed shear-driven dynamos. Part 1. Asymptotic analysis
-
- Published online by Cambridge University Press:
- 10 April 2019, pp. 176-211
-
- Article
- Export citation
Stokes resistance of a solid cylinder near a superhydrophobic surface. Part 1. Grooves perpendicular to cylinder axis
-
- Published online by Cambridge University Press:
- 10 April 2019, pp. 212-243
-
- Article
- Export citation
Fluctuation of magnitude of wave loads for a long array of bottom-mounted cylinders
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 244-285
-
- Article
- Export citation
The dynamics of an insulating plate over a thermally convecting fluid and its implication for continent movement over convective mantle
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 286-315
-
- Article
- Export citation
Equilibrium positions of the elasto-inertial particle migration in rectangular channel flow of Oldroyd-B viscoelastic fluids
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 316-340
-
- Article
- Export citation
Nonlinear exact coherent structures in pipe flow and their instabilities
-
- Published online by Cambridge University Press:
- 15 April 2019, pp. 341-368
-
- Article
- Export citation
Evolutionary shape optimisation enhances the lift coefficient of rotating wing geometries
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 369-384
-
- Article
- Export citation
Acoustic theory of the many-bladed contra-rotating propeller: analysis of the effects of blade sweep on wake interaction noise
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 385-427
-
- Article
- Export citation