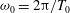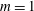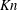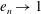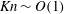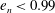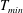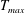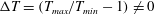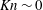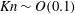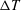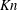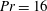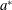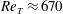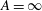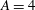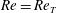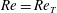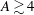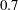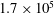Focus on Fluids
Electrokinetics meets electrohydrodynamics
-
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Hydraulic jumps in a shallow flow down a slightly inclined substrate
-
- Published online by Cambridge University Press:
- 30 September 2015, pp. 5-24
-
- Article
- Export citation
On the kurtosis of deep-water gravity waves
-
- Published online by Cambridge University Press:
- 30 September 2015, pp. 25-36
-
- Article
- Export citation
Vorticity reconnection during vortex cutting by a blade
-
- Published online by Cambridge University Press:
- 01 October 2015, pp. 37-62
-
- Article
- Export citation
Precession of a rapidly rotating cylinder flow: traverse through resonance
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 63-98
-
- Article
- Export citation
On Knudsen-minimum effect and temperature bimodality in a dilute granular Poiseuille flow
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 99-126
-
- Article
- Export citation
On the selection of viscosity to suppress the Saffman–Taylor instability in a radially spreading annulus
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 127-143
-
- Article
- Export citation
Inertia–gravity waves in a liquid-filled, differentially heated, rotating annulus
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 144-177
-
- Article
- Export citation
Wave field and zonal flow of a librating disk
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 178-208
-
- Article
- Export citation
Partial coalescence from bubbles to drops
-
- Published online by Cambridge University Press:
- 07 October 2015, pp. 209-239
-
- Article
- Export citation
Direct control of the small-scale energy balance in two-dimensional fluid dynamics
-
- Published online by Cambridge University Press:
- 07 October 2015, pp. 240-259
-
- Article
- Export citation
Heat/mass transport in shear flow over a heterogeneous surface with first-order surface-reactive domains
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 260-299
-
- Article
- Export citation
U-shaped fairings suppress vortex-induced vibrations for cylinders in cross-flow
-
- Published online by Cambridge University Press:
- 09 October 2015, pp. 300-332
-
- Article
- Export citation
Energy-consistent entrainment relations for jets and plumes
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 333-355
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic descriptions of oblique coherent structures in shear flows
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 356-367
-
- Article
- Export citation
Localized turbulence structures in transitional rectangular-duct flow
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 368-379
-
- Article
- Export citation
Physical and scale-by-scale analysis of Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 380-404
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The evolution of segregation in dense inclined flows of binary mixtures of spheres
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 405-429
-
- Article
- Export citation
Exact coherent states and connections to turbulent dynamics in minimal channel flow
-
- Published online by Cambridge University Press:
- 08 October 2015, pp. 430-454
-
- Article
- Export citation
Filling box flows in porous media
-
- Published online by Cambridge University Press:
- 09 October 2015, pp. 455-478
-
- Article
- Export citation