The numerical simulation of gravity-driven flow of smooth inelastic hard disks through a channel, dubbed ‘granular’ Poiseuille flow, is conducted using event-driven techniques. We find that the variation of the mass-flow rate (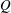$Q$) with Knudsen number (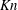$Kn$) can be non-monotonic in the elastic limit (i.e. the restitution coefficient 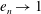$e_{n}\rightarrow 1$) in channels with very smooth walls. The Knudsen-minimum effect (i.e. the minimum flow rate occurring at 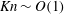$Kn\sim O(1)$ for the Poiseuille flow of a molecular gas) is found to be absent in a granular gas with 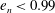$e_{n}<0.99$, irrespective of the value of the wall roughness. Another rarefaction phenomenon, the bimodality of the temperature profile, with a local minimum (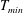$T_{\mathit{min}}$) at the channel centerline and two symmetric maxima (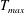$T_{\mathit{max}}$) away from the centerline, is also studied. We show that the inelastic dissipation is responsible for the onset of temperature bimodality (i.e. the ‘excess’ temperature, 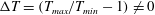${\rm\Delta}T=(T_{\mathit{max}}/T_{\mathit{min}}-1)\neq 0$) near the continuum limit (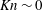$Kn\sim 0$), but the rarefaction being its origin (as in the molecular gas) holds beyond 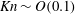$Kn\sim O(0.1)$. The dependence of the excess temperature 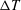${\rm\Delta}T$ on the restitution coefficient is compared with the predictions of a kinetic model, with reasonable agreement in the appropriate limit. The competition between dissipation and rarefaction seems to be responsible for the observed dependence of both the mass-flow rate and the temperature bimodality on 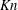$Kn$ and 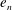$e_{n}$ in this flow. The validity of the Navier–Stokes-order hydrodynamics for granular Poiseuille flow is discussed with reference to the prediction of bimodal temperature profiles and related surrogates.