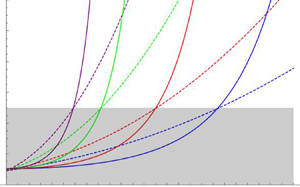
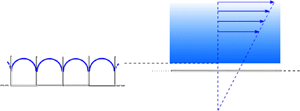
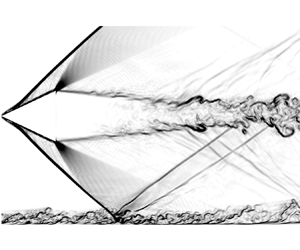
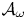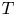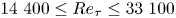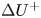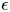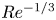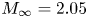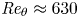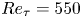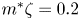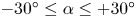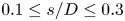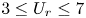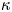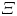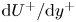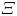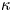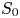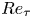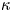doi:10.1017/jfm.2023.462 Poulain et al. Sliding, vibrating and swinging droplets on an oscillating fibre
JFM Rapids
Towards a finite-time singularity of the Navier–Stokes equations. Part 3. Maximal vorticity amplification
-
- Published online by Cambridge University Press:
- 12 July 2023, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Towards decoupling the effects of permeability and roughness on turbulent boundary layers
-
- Published online by Cambridge University Press:
- 12 July 2023, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Highly singular slip length for longitudinal shear flow over a dense bubble mattress
-
- Published online by Cambridge University Press:
- 18 July 2023, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Velocity and acceleration statistics of heavy spheroidal particles in turbulence
-
- Published online by Cambridge University Press:
- 18 July 2023, R4
-
- Article
- Export citation
Thermo-osmotic flow in slit channels with boundary slip: giant flow amplification between polarized graphene surfaces
-
- Published online by Cambridge University Press:
- 24 July 2023, R5
-
- Article
- Export citation
JFM Papers
Causality analysis of large-scale structures in the flow around a wall-mounted square cylinder
-
- Published online by Cambridge University Press:
- 11 July 2023, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
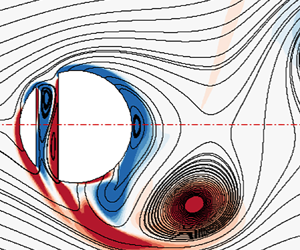
Linear stability analysis of wake vortices by a spectral method using mapped Legendre functions
-
- Published online by Cambridge University Press:
- 11 July 2023, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On wall pressure fluctuations in conical shock wave/turbulent boundary layer interaction
-
- Published online by Cambridge University Press:
- 11 July 2023, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global stability analysis of elastic aircraft in edge-of-the-envelope flow
-
- Published online by Cambridge University Press:
- 12 July 2023, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evolution of an elastic blister in the presence of sloping topography
-
- Published online by Cambridge University Press:
- 12 July 2023, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Engineering of branched fluidic networks that minimise energy dissipation
-
- Published online by Cambridge University Press:
- 12 July 2023, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Influence of heterogeneity or shape on the locomotion of a caged squirmer
-
- Published online by Cambridge University Press:
- 12 July 2023, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How electrostatic forces affect particle behaviour in turbulent channel flows
-
- Published online by Cambridge University Press:
- 13 July 2023, A8
-
- Article
- Export citation
Vorticity transport in a turbulent channel flow subjected to streamwise travelling waves
-
- Published online by Cambridge University Press:
- 13 July 2023, A9
-
- Article
- Export citation
Three-dimensional numerical investigation of a transversely oscillating slotted cylinder and its applications in energy harvesting
-
- Published online by Cambridge University Press:
- 13 July 2023, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On high-Taylor-number Taylor vortices
-
- Published online by Cambridge University Press:
- 17 July 2023, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wind-generated waves on a water layer of finite depth
-
- Published online by Cambridge University Press:
- 17 July 2023, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propulsion due to thermal streaming
-
- Published online by Cambridge University Press:
- 17 July 2023, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slippery rheotaxis: new regimes for guiding wall-bound microswimmers
-
- Published online by Cambridge University Press:
- 17 July 2023, A14
-
- Article
- Export citation
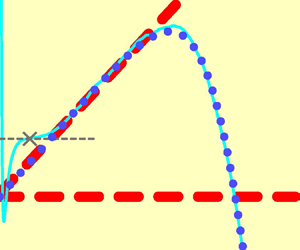
The hunt for the Kármán ‘constant’ revisited
-
- Published online by Cambridge University Press:
- 17 July 2023, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation