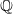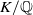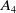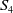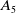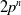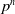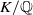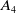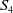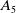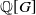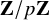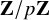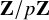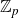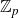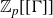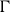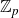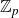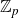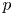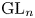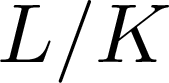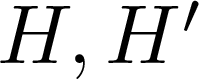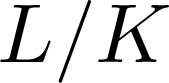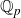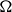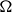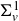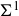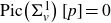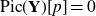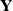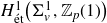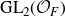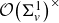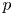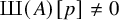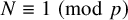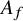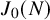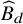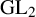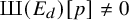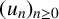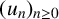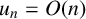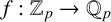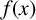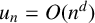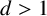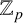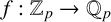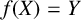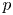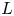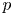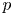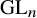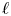101 results in 11Sxx
BPS invariants from p-adic integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1525-1550
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
WEIERSTRASS ZETA FUNCTIONS AND p-ADIC LINEAR RELATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-10
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
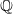 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smith theory and cyclic base change functoriality
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of fine Selmer groups over
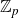 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 287-308
- Print publication:
- March 2024
-
- Article
- Export citation
On the derived category of the Iwahori–Hecke algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 04 May 2023, pp. 1042-1110
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ρ-conjugate Hopf–Galois structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 288-304
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Detecting and describing ramification for structured ring spectra
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 529-554
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The error term in the truncated Perron formula for the logarithm of an L-function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 1122-1134
- Print publication:
- December 2023
-
- Article
- Export citation
The explicit Zelevinsky–Aubert duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 20 February 2023, pp. 380-418
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elements of prime order in Tate–Shafarevich groups of abelian varieties over
 ${\mathbb Q}$
${\mathbb Q}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 November 2022, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON p-ADIC INTERPOLATION IN TWO OF MAHLER’S PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 69-80
- Print publication:
- August 2023
-
- Article
- Export citation
GENERALIZED ZETA INTEGRALS ON CERTAIN REAL PREHOMOGENEOUS VECTOR SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 50-87
- Print publication:
- March 2023
-
- Article
- Export citation
MODEL THEORY OF GALOIS ACTIONS OF TORSION ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 2943-2985
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sum expressions for Kubota–Leopoldt $p$
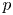 -adic $L$
-adic $L$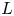 -functions
-functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 460-479
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kottwitz conjecture for local shtuka spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF FIELDS WITH FINITE GROUP SCHEME ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1443-1468
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trace and Künneth formulas for singularity categories and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 483-528
- Print publication:
- March 2022
-
- Article
- Export citation
Uniform perfectness of the Berkovich Julia sets in non-archimedean dynamics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 573-590
- Print publication:
- November 2022
-
- Article
- Export citation