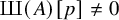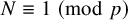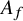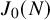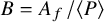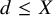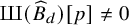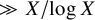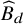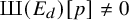1 Introduction
Let A be an abelian variety over
![]() ${\mathbb Q}$
. The Tate–Shafarevich group of A is the abelian group
${\mathbb Q}$
. The Tate–Shafarevich group of A is the abelian group

classifying
![]() ${\mathbb Q}$
-isomorphism classes of A-torsors that are isomorphic to A over
${\mathbb Q}$
-isomorphism classes of A-torsors that are isomorphic to A over
![]() $\mathbb Q_{\ell }$
for every prime
$\mathbb Q_{\ell }$
for every prime
![]() $\ell $
, including the infinite prime
$\ell $
, including the infinite prime
![]() $\ell = \infty $
. Much is conjectured but little is known about the structure of this group. Famously, the Birch and Swinnerton-Dyer conjecture predicts that
$\ell = \infty $
. Much is conjectured but little is known about the structure of this group. Famously, the Birch and Swinnerton-Dyer conjecture predicts that
is finite. On the other hand, heuristics suggest that, for each prime p, a positive proportion of elliptic curves
![]() $E/{\mathbb Q}$
, ordered by height, have
$E/{\mathbb Q}$
, ordered by height, have
[Reference DelaunayDel07, Reference Poonen and RainsPR12, Reference Bhargava, Kane, Lenstra, Poonen and RainsBKL+15], and one expects something similar for abelian varieties of higher dimension.
In stark contrast to these expectations, it seems to be an open question whether, for each prime p, there exists even a single elliptic curve over
![]() ${\mathbb Q}$
with
${\mathbb Q}$
with
![]() . There are constructions of elliptic curves and higher-dimensional abelian varieties A over number fields K with
. There are constructions of elliptic curves and higher-dimensional abelian varieties A over number fields K with
![]() [Reference KloostermanKlo05, Reference Clark and SharifCS10, Reference CreutzCre11], although the degree of K grows as a function of p in these results. Taking Weil restrictions of these examples gives abelian varieties
[Reference KloostermanKlo05, Reference Clark and SharifCS10, Reference CreutzCre11], although the degree of K grows as a function of p in these results. Taking Weil restrictions of these examples gives abelian varieties
![]() $A'/{\mathbb Q}$
with
$A'/{\mathbb Q}$
with
![]() . However, there again seem to be no known examples of geometrically simple abelian varieties
. However, there again seem to be no known examples of geometrically simple abelian varieties
![]() $A/{\mathbb Q}$
with
$A/{\mathbb Q}$
with
![]() , for large primes p. The purpose of this paper is to provide such examples.
, for large primes p. The purpose of this paper is to provide such examples.
Theorem 1.1. For each prime p, there exists a geometrically simple abelian variety
![]() $A/{\mathbb Q}$
such that
$A/{\mathbb Q}$
such that
![]() .
.
In fact, for each p, we exhibit infinitely many such
![]() $A/{\mathbb Q}$
in distinct
$A/{\mathbb Q}$
in distinct
![]() $\overline {\mathbb Q}$
-isogeny classes. Our examples arise from optimal quotients
$\overline {\mathbb Q}$
-isogeny classes. Our examples arise from optimal quotients
![]() $A_f$
of the modular Jacobian
$A_f$
of the modular Jacobian
![]() $J_0(N)$
, attached to weight two newforms
$J_0(N)$
, attached to weight two newforms
![]() $f \in S_2(\Gamma _0(N))$
of prime level N.
$f \in S_2(\Gamma _0(N))$
of prime level N.
Theorem 1.2. Let N be a prime, and let
![]() $p \geq 3$
be a prime divisor of
$p \geq 3$
be a prime divisor of
![]() $(N-1)/\gcd (12,N-1)$
. Let
$(N-1)/\gcd (12,N-1)$
. Let
![]() $A_f$
be any optimal quotient of
$A_f$
be any optimal quotient of
![]() $J_0(N)$
containing a point
$J_0(N)$
containing a point
![]() $P \in A_f({\mathbb Q})$
of order p. Let
$P \in A_f({\mathbb Q})$
of order p. Let
![]() $B = A_f/\langle P \rangle $
, let
$B = A_f/\langle P \rangle $
, let
![]() $\phi : A_f\to B$
be the canonical isogeny, and let
$\phi : A_f\to B$
be the canonical isogeny, and let
![]() $\widehat \phi \colon \widehat B \to \widehat A_f$
be the dual isogeny. Then
$\widehat \phi \colon \widehat B \to \widehat A_f$
be the dual isogeny. Then
where
![]() $\widehat B_d$
is the dth quadratic twist of
$\widehat B_d$
is the dth quadratic twist of
![]() $\widehat B$
, for each
$\widehat B$
, for each
![]() $d \in {\mathbb Z}$
.
$d \in {\mathbb Z}$
.
Theorem 1.1 follows immediately from Theorem 1.2. Indeed, the abelian varieties
![]() $A_f$
and
$A_f$
and
![]() $\widehat B_d$
are geometrically simple [Reference RibetRib75, Corollary 1.4]; and for any prime p dividing
$\widehat B_d$
are geometrically simple [Reference RibetRib75, Corollary 1.4]; and for any prime p dividing
![]() $\frac {N-1}{(12,N-1)}$
, there exists at least one newform
$\frac {N-1}{(12,N-1)}$
, there exists at least one newform
![]() $f \in S_2(\Gamma _0(N))$
such that
$f \in S_2(\Gamma _0(N))$
such that
![]() $A_f({\mathbb Q})$
contains a point of order p [Reference EmertonEme03, Theorem B]. Hence, given a prime p, it suffices to apply Theorem 1.2 to any prime
$A_f({\mathbb Q})$
contains a point of order p [Reference EmertonEme03, Theorem B]. Hence, given a prime p, it suffices to apply Theorem 1.2 to any prime
![]() $N\equiv 1\ \pmod p$
. Moreover, Dirichlet’s theorem on primes in arithmetic progressions guarantees that there are infinitely many such N. Since N is prime,
$N\equiv 1\ \pmod p$
. Moreover, Dirichlet’s theorem on primes in arithmetic progressions guarantees that there are infinitely many such N. Since N is prime,
![]() $J_0(N)$
is semistable with conductor a power of N, and we see that different choices of N give geometrically non-isogenous abelian varieties
$J_0(N)$
is semistable with conductor a power of N, and we see that different choices of N give geometrically non-isogenous abelian varieties
![]() $A/{\mathbb Q}$
with
$A/{\mathbb Q}$
with
![]() .
.
The dimensions of the abelian varieties A we produce grow with p. Indeed, the Weil conjectures imply that
![]() $\dim A_f \geq \frac {\log p}{2\log (1+\sqrt 2)}$
[Reference MazurMaz77, Proposition 7.2]; in particular,
$\dim A_f \geq \frac {\log p}{2\log (1+\sqrt 2)}$
[Reference MazurMaz77, Proposition 7.2]; in particular,
![]() $A_f$
is not an elliptic curve if
$A_f$
is not an elliptic curve if
![]() $p \geq 7$
. One could give a very crude upper bound for the minimal dimension of an A with
$p \geq 7$
. One could give a very crude upper bound for the minimal dimension of an A with
![]() by combining bounds for the smallest prime
by combining bounds for the smallest prime
![]() $N\equiv 1\ \pmod p$
with well-known bounds on the dimension of
$N\equiv 1\ \pmod p$
with well-known bounds on the dimension of
![]() $J_0(N)$
.
$J_0(N)$
.
Our proof of Theorem 1.2 is fairly short but uses several deep inputs. First, we prove that if
![]() $\phi :A\to B$
is a p-isogeny of abelian varieties, whose Selmer ratio
$\phi :A\to B$
is a p-isogeny of abelian varieties, whose Selmer ratio
![]() $c(\phi )$
equals
$c(\phi )$
equals
![]() $p^i$
(see Definition 2.2), then there exists an explicit, positive density set of squarefree integers
$p^i$
(see Definition 2.2), then there exists an explicit, positive density set of squarefree integers
![]() $\Sigma ^+$
such that
$\Sigma ^+$
such that
![]() for all but finitely many quadratic twists
for all but finitely many quadratic twists
![]() $A_d$
with
$A_d$
with
![]() $d\in \Sigma ^+$
(Theorem 2.4). Our proof uses techniques from Galois cohomology, particularly the Greenberg–Wiles formula.
$d\in \Sigma ^+$
(Theorem 2.4). Our proof uses techniques from Galois cohomology, particularly the Greenberg–Wiles formula.
In the case that
![]() $A=A_f$
is an optimal quotient of
$A=A_f$
is an optimal quotient of
![]() $J_0(N)$
, we then invoke nonvanishing results for special values of L-functions, due to Bump–Friedberg–Hoffstein and Ono–Skinner [Reference Bump, Friedberg and HoffsteinBFH90, Reference Ono and SkinnerOS98], to show that
$J_0(N)$
, we then invoke nonvanishing results for special values of L-functions, due to Bump–Friedberg–Hoffstein and Ono–Skinner [Reference Bump, Friedberg and HoffsteinBFH90, Reference Ono and SkinnerOS98], to show that
![]() $L(f_d,s) \neq 0$
for many quadratic twists
$L(f_d,s) \neq 0$
for many quadratic twists
![]() $f_d$
of f. By work of Gross–Zagier and Kolyvagin–Logachev [Reference Gross and ZagierGZ86, Reference Kolyvagin and LogachëvKL89] or Kato [Reference KatoKat04], we have
$f_d$
of f. By work of Gross–Zagier and Kolyvagin–Logachev [Reference Gross and ZagierGZ86, Reference Kolyvagin and LogachëvKL89] or Kato [Reference KatoKat04], we have
![]() $\operatorname {\mathrm {rk}} \widehat B_d({\mathbb Q}) = 0$
for such d. It follows that if
$\operatorname {\mathrm {rk}} \widehat B_d({\mathbb Q}) = 0$
for such d. It follows that if
![]() $A=A_f$
is an optimal quotient of
$A=A_f$
is an optimal quotient of
![]() $J_0(N)$
that admits a p-isogeny
$J_0(N)$
that admits a p-isogeny
![]() $\phi \colon A \to B$
such that
$\phi \colon A \to B$
such that
![]() $c(\phi )\ge p^2$
, then
$c(\phi )\ge p^2$
, then
![]() for infinitely many quadratic twists
for infinitely many quadratic twists
![]() $A_d$
(Theorem 3.1).
$A_d$
(Theorem 3.1).
In Section 4, we specialise to prime N, where we use Mazur’s study of the Eisenstein ideal [Reference MazurMaz77, Reference EmertonEme03] to show that the condition on
![]() $c(\phi )$
is always satisfied, thereby proving Theorem 1.2. Our computation of
$c(\phi )$
is always satisfied, thereby proving Theorem 1.2. Our computation of
![]() $c(\phi )$
is a generalisation of [Reference ShnidmanShn21, §6], which was for the prime
$c(\phi )$
is a generalisation of [Reference ShnidmanShn21, §6], which was for the prime
![]() $p = 3$
.
$p = 3$
.
In the case of elliptic curves, we prove an even stronger bound than the one in Theorem 1.2, by invoking recent work of Smith [Reference SmithSmi20] instead of results on L-functions. In Section 5, we prove
Theorem 1.3. Let E be an elliptic curve over
![]() ${\mathbb Q}$
with a degree p isogeny
${\mathbb Q}$
with a degree p isogeny
![]() $\phi :E \to E'$
, for some prime
$\phi :E \to E'$
, for some prime
![]() $p \geq 3$
. Assume that
$p \geq 3$
. Assume that
![]() $c(\phi ) \geq p^2$
and that
$c(\phi ) \geq p^2$
and that
![]() $E[2]({\mathbb Q}) \neq {\mathbb Z}/2{\mathbb Z}$
. Then for a positive proportion of squarefree integers d, we have
$E[2]({\mathbb Q}) \neq {\mathbb Z}/2{\mathbb Z}$
. Then for a positive proportion of squarefree integers d, we have
![]() .
.
The hypothesis
![]() $c(\phi )\ge p^2$
applies to ‘most’ quadratic twist families of p-isogenies of elliptic curves with
$c(\phi )\ge p^2$
applies to ‘most’ quadratic twist families of p-isogenies of elliptic curves with
![]() $p \ge 3$
, in a certain sense (see Proposition 5.1).
$p \ge 3$
, in a certain sense (see Proposition 5.1).
For each elliptic curve E in Theorem 1.3, we can give an explicit lower bound on the proportion of d such that
![]() . Sometimes these bounds are larger than those predicted by a naïve generalisation of the heuristics of Delaunay [Reference DelaunayDel01] and Poonen–Rains [Reference Poonen and RainsPR12]. For example, in Section 6, we prove that for the elliptic curve
. Sometimes these bounds are larger than those predicted by a naïve generalisation of the heuristics of Delaunay [Reference DelaunayDel01] and Poonen–Rains [Reference Poonen and RainsPR12]. For example, in Section 6, we prove that for the elliptic curve
![]() $E :y^2 +y = x^3-x^2-7820x-263580$
with LMFDB label 11.a1, we have
$E :y^2 +y = x^3-x^2-7820x-263580$
with LMFDB label 11.a1, we have
![]() for at least
for at least
![]() $22.9\%$
of squarefree integers d. This example shows that the heuristics of Delaunay and Poonen–Rains on distributions of p-Selmer groups need to be modified when applied to quadratic twist families of elliptic curves with a rational p-isogeny.
$22.9\%$
of squarefree integers d. This example shows that the heuristics of Delaunay and Poonen–Rains on distributions of p-Selmer groups need to be modified when applied to quadratic twist families of elliptic curves with a rational p-isogeny.
In [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21, Conjecture 1], Bhargava, Klagsbrun, Lemke Oliver and the first author state a conjecture that for any abelian variety
![]() $A/{\mathbb Q}$
, we should have
$A/{\mathbb Q}$
, we should have
![]() for a positive proportion of squarefree integers d. They prove special cases of this conjecture, without invoking Smith’s work, when one of E or
for a positive proportion of squarefree integers d. They prove special cases of this conjecture, without invoking Smith’s work, when one of E or
![]() $E'$
admits an additional
$E'$
admits an additional
![]() $3$
-isogeny, in addition to a p-isogeny. In general, most known systematic constructions of elements in
$3$
-isogeny, in addition to a p-isogeny. In general, most known systematic constructions of elements in
![]() over
over
![]() ${\mathbb Q}$
exploit either multiple isogenies or the Cassels–Tate pairing; see, for example, [Reference CasselsCas64, Reference FisherFis01, Reference FlynnFly19, Reference ShnidmanShn21, Reference Bhargava and HoBH22, Reference Bruin, Flynn and ShnidmanBFS21]. One exception is a theorem of Balog–Ono [Reference Balog and OnoBO03, Theorem 2], which applies to a large class of elliptic curves
${\mathbb Q}$
exploit either multiple isogenies or the Cassels–Tate pairing; see, for example, [Reference CasselsCas64, Reference FisherFis01, Reference FlynnFly19, Reference ShnidmanShn21, Reference Bhargava and HoBH22, Reference Bruin, Flynn and ShnidmanBFS21]. One exception is a theorem of Balog–Ono [Reference Balog and OnoBO03, Theorem 2], which applies to a large class of elliptic curves
![]() $E/{\mathbb Q}$
with a point of order p. As with our proof of Theorem 1.2, their proof relies on nonvanishing results for L-functions, but to prove
$E/{\mathbb Q}$
with a point of order p. As with our proof of Theorem 1.2, their proof relies on nonvanishing results for L-functions, but to prove
![]() $\operatorname {\mathrm {Sel}}_p(E_d) \neq 0$
, they instead use nonvanishing results for class groups. This leads to the weaker bound
$\operatorname {\mathrm {Sel}}_p(E_d) \neq 0$
, they instead use nonvanishing results for class groups. This leads to the weaker bound
![]() . Thus, even in the special case of elliptic curves, we improve significantly on the known quantitative results whenever our method applies.
. Thus, even in the special case of elliptic curves, we improve significantly on the known quantitative results whenever our method applies.
2 Selmer groups of abelian varieties with a
 $p$
-isogeny
$p$
-isogeny
Let
![]() $\phi \colon A \to B$
be an isogeny of abelian varieties over
$\phi \colon A \to B$
be an isogeny of abelian varieties over
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
2.1 Selmer groups and the Selmer ratio
Definition 2.1. The
![]() $\phi $
-Selmer group is
$\phi $
-Selmer group is
 $$\begin{align*}\operatorname{\mathrm{Sel}}(\phi) = \ker\left(H^1({\mathbb Q}, A[\phi]) \to \prod_{\ell \leq \infty} H^1(\mathbb Q_{\ell}, A)\right). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Sel}}(\phi) = \ker\left(H^1({\mathbb Q}, A[\phi]) \to \prod_{\ell \leq \infty} H^1(\mathbb Q_{\ell}, A)\right). \end{align*}$$
In the special case
![]() $A = B$
and
$A = B$
and
![]() $\phi = [p]_A$
, we write
$\phi = [p]_A$
, we write
![]() $\operatorname {\mathrm {Sel}}_p(A)$
instead of
$\operatorname {\mathrm {Sel}}_p(A)$
instead of
![]() $\operatorname {\mathrm {Sel}}([p]_A)$
.
$\operatorname {\mathrm {Sel}}([p]_A)$
.
Definition 2.2. For
![]() $\ell $
a finite or infinite prime, define the local Selmer ratio
$\ell $
a finite or infinite prime, define the local Selmer ratio
When
![]() $\ell = \infty $
, we use the convention that
$\ell = \infty $
, we use the convention that
![]() ${\mathbb Q}_{\infty } = {\mathbb R}$
. We then define the global Selmer ratio
${\mathbb Q}_{\infty } = {\mathbb R}$
. We then define the global Selmer ratio
These Selmer ratios were defined in [Reference Bhargava, Elkies and ShnidmanBES20] but were already studied in [Reference CasselsCas65] under a slightly different guise. The notation is meant to recall the Tamagawa number
![]() $c_{\ell }(X)$
of an abelian variety X over
$c_{\ell }(X)$
of an abelian variety X over
![]() ${\mathbb Q}_{\ell }$
. Indeed, the following lemma shows that for all but finitely many primes
${\mathbb Q}_{\ell }$
. Indeed, the following lemma shows that for all but finitely many primes
![]() $\ell $
, we have
$\ell $
, we have
![]() $c_{\ell }(\phi ) = c_{\ell }(B)/c_{\ell }(A)$
.
$c_{\ell }(\phi ) = c_{\ell }(B)/c_{\ell }(A)$
.
Lemma 2.3. For any finite prime
![]() $\ell $
, we have
$\ell $
, we have
where
![]() $\gamma _{\phi , \ell }^{-1}$
is the normalised absolute value of the determinant of the map
$\gamma _{\phi , \ell }^{-1}$
is the normalised absolute value of the determinant of the map
![]() $\mathrm {Lie}(\mathcal {A}) \to \mathrm {Lie}(\mathcal {B})$
on tangent spaces of the Néron models over
$\mathrm {Lie}(\mathcal {A}) \to \mathrm {Lie}(\mathcal {B})$
on tangent spaces of the Néron models over
![]() ${\mathbb Z}_{\ell }$
. In particular, if
${\mathbb Z}_{\ell }$
. In particular, if
![]() $\ell \nmid \deg (\phi )$
, then
$\ell \nmid \deg (\phi )$
, then
![]() $\gamma _{\phi , \ell }=1$
.
$\gamma _{\phi , \ell }=1$
.
Proof. This lemma is [Reference SchaeferSch96, Lemma 3.8]. Recall that
![]() $c_{\ell }(A) = \#A({\mathbb Q}_{\ell })/A_0({\mathbb Q}_{\ell })$
, where
$c_{\ell }(A) = \#A({\mathbb Q}_{\ell })/A_0({\mathbb Q}_{\ell })$
, where
![]() $A_0({\mathbb Q}_{\ell })$
is the subgroup of points that reduce to the identity component in the special fibre of the Néron model
$A_0({\mathbb Q}_{\ell })$
is the subgroup of points that reduce to the identity component in the special fibre of the Néron model
![]() $\mathcal {A}$
of A.
$\mathcal {A}$
of A.
The local Tamagawa numbers
![]() $c_{\ell }(A), c_{\ell }(B)$
are equal to 1 for all primes
$c_{\ell }(A), c_{\ell }(B)$
are equal to 1 for all primes
![]() $\ell $
of good reduction. Hence, we have
$\ell $
of good reduction. Hence, we have
![]() $c_{\ell }(\phi ) = 1$
for all but finitely many primes, so the global Selmer ratio
$c_{\ell }(\phi ) = 1$
for all but finitely many primes, so the global Selmer ratio
![]() $c(\phi ) = \prod _{\ell } c_{\ell }(\phi )$
is well-defined. Moreover, if
$c(\phi ) = \prod _{\ell } c_{\ell }(\phi )$
is well-defined. Moreover, if
![]() $\phi $
has prime degree p, then
$\phi $
has prime degree p, then
![]() $c(\phi )$
is an integer power of p.
$c(\phi )$
is an integer power of p.
2.2 Lower bounds on Selmer groups
Let N be the radical of the conductor of A. Thus, a prime
![]() $\ell $
divides N if and only if A has bad reduction at
$\ell $
divides N if and only if A has bad reduction at
![]() $\ell $
.
$\ell $
.
Let
![]() $\Sigma ^+$
be the set of positive squarefree integers d such that
$\Sigma ^+$
be the set of positive squarefree integers d such that
![]() $d \in {\mathbb Z}_{\ell }^{\times 2}$
for all primes
$d \in {\mathbb Z}_{\ell }^{\times 2}$
for all primes
![]() $\ell \mid pN$
. For any squarefree
$\ell \mid pN$
. For any squarefree
![]() $d\in {\mathbb Z}$
, write
$d\in {\mathbb Z}$
, write
![]() $\phi _d :A_d\to B_d$
for the dth quadratic twist of
$\phi _d :A_d\to B_d$
for the dth quadratic twist of
![]() $\phi $
, which again has degree p.
$\phi $
, which again has degree p.
Theorem 2.4. Suppose that
![]() $\phi \colon A\to B$
is a degree p isogeny, and write
$\phi \colon A\to B$
is a degree p isogeny, and write
![]() $c(\phi ) = p^i$
for some
$c(\phi ) = p^i$
for some
![]() $i \in {\mathbb Z}$
. Then for all but finitely many
$i \in {\mathbb Z}$
. Then for all but finitely many
![]() $d \in \Sigma ^+$
, we have
$d \in \Sigma ^+$
, we have
![]() $\dim _{\mathbb F_p}\operatorname {\mathrm {Sel}}_p(A_d)\geq i$
, and hence
$\dim _{\mathbb F_p}\operatorname {\mathrm {Sel}}_p(A_d)\geq i$
, and hence
The proof will require several lemmas.
Lemma 2.5. If
![]() $\ell \nmid pN\infty $
, then
$\ell \nmid pN\infty $
, then
![]() $c_{\ell }(\phi _d) = 1$
for all nonzero
$c_{\ell }(\phi _d) = 1$
for all nonzero
![]() $d\in {\mathbb Z}$
.
$d\in {\mathbb Z}$
.
Proof. Let
![]() $\chi _d :\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}_{\ell }/\mathbb Q_{\ell })\to \mathbb F_p^{\times }$
denote the character corresponding to the (possibly trivial) extension
$\chi _d :\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}_{\ell }/\mathbb Q_{\ell })\to \mathbb F_p^{\times }$
denote the character corresponding to the (possibly trivial) extension
![]() $\mathbb Q_{\ell }(\sqrt {d})/\mathbb Q_{\ell }$
. If
$\mathbb Q_{\ell }(\sqrt {d})/\mathbb Q_{\ell }$
. If
![]() $\chi _d$
is unramified, then
$\chi _d$
is unramified, then
![]() $A_d$
has good reduction over
$A_d$
has good reduction over
![]() $\mathbb Q_{\ell }$
, and
$\mathbb Q_{\ell }$
, and
![]() $c_{\ell }(\phi _d) = c_{\ell }(B_d)/c_{\ell }(A_d) = 1$
by Lemma 2.3. Assume now that
$c_{\ell }(\phi _d) = c_{\ell }(B_d)/c_{\ell }(A_d) = 1$
by Lemma 2.3. Assume now that
![]() $\chi _d$
is ramified (and, in particular, nontrivial). Since A has good reduction over
$\chi _d$
is ramified (and, in particular, nontrivial). Since A has good reduction over
![]() $\mathbb Q_{\ell }$
, the extension
$\mathbb Q_{\ell }$
, the extension
![]() $\mathbb Q_{\ell }(A[\phi ])/\mathbb Q_{\ell }$
is unramified. Hence, the
$\mathbb Q_{\ell }(A[\phi ])/\mathbb Q_{\ell }$
is unramified. Hence, the
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}_{\ell }/\mathbb Q_{\ell })$
-action on
$\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}_{\ell }/\mathbb Q_{\ell })$
-action on
![]() $A_d[\phi _d]\simeq A[\phi ] \otimes _{\mathbb F_p} \chi _d$
is via a nontrivial character
$A_d[\phi _d]\simeq A[\phi ] \otimes _{\mathbb F_p} \chi _d$
is via a nontrivial character
![]() $\widetilde \chi _d$
. Thus
$\widetilde \chi _d$
. Thus
 $$\begin{align*}c_{\ell}(\phi_d) = \frac{\#\operatorname{\mathrm{im}} (B_d(\mathbb Q_{\ell})\to H^1(\mathbb Q_{\ell}, \widetilde\chi_d))}{\#H^0(\mathbb Q_{\ell}, \widetilde\chi_d)}. \end{align*}$$
$$\begin{align*}c_{\ell}(\phi_d) = \frac{\#\operatorname{\mathrm{im}} (B_d(\mathbb Q_{\ell})\to H^1(\mathbb Q_{\ell}, \widetilde\chi_d))}{\#H^0(\mathbb Q_{\ell}, \widetilde\chi_d)}. \end{align*}$$
The denominator is 1 since
![]() $\widetilde \chi _d$
is nontrivial. Let
$\widetilde \chi _d$
is nontrivial. Let
![]() $\epsilon :\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}_{\ell }/\mathbb Q_{\ell })\to \mathbb F_p^{\times }$
be the mod p cyclotomic character, which is unramified. We have
$\epsilon :\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}_{\ell }/\mathbb Q_{\ell })\to \mathbb F_p^{\times }$
be the mod p cyclotomic character, which is unramified. We have
![]() $\# H^1(\mathbb Q_{\ell }, \widetilde \chi _d) = \# H^0(\mathbb Q_{\ell },\widetilde \chi _d)\#H^0(\mathbb Q_{\ell }, \widetilde \chi _d^{-1}\epsilon ) = 1$
, by local Tate duality [Reference MilneMil06, Corollary I.2.3] and the Euler characteristic formula [Reference MilneMil06, Theorem I.2.8]. Hence,
$\# H^1(\mathbb Q_{\ell }, \widetilde \chi _d) = \# H^0(\mathbb Q_{\ell },\widetilde \chi _d)\#H^0(\mathbb Q_{\ell }, \widetilde \chi _d^{-1}\epsilon ) = 1$
, by local Tate duality [Reference MilneMil06, Corollary I.2.3] and the Euler characteristic formula [Reference MilneMil06, Theorem I.2.8]. Hence,
![]() $c_{\ell }(\phi _d)=1$
.
$c_{\ell }(\phi _d)=1$
.
Lemma 2.6. We have
![]() $c_{\infty }(\phi ) = \#A[\phi ](\mathbb R)^{-1}$
.
$c_{\infty }(\phi ) = \#A[\phi ](\mathbb R)^{-1}$
.
Proof. We have
Since
![]() $\#A[\phi ] = p$
is odd, we have
$\#A[\phi ] = p$
is odd, we have
![]() $H^1(\operatorname {\mathrm {Gal}}(\mathbb C/\mathbb R), A[\phi ]) = 0$
. Hence,
$H^1(\operatorname {\mathrm {Gal}}(\mathbb C/\mathbb R), A[\phi ]) = 0$
. Hence,
To prove Theorem 2.4, we will use the Greenberg–Wiles formula [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 8.7.9], which is a consequence of Poitou–Tate duality. If
![]() $\psi \colon X \to Y$
is an isogeny, it relates the size of
$\psi \colon X \to Y$
is an isogeny, it relates the size of
![]() $\operatorname {\mathrm {Sel}}(\psi )$
to the size of
$\operatorname {\mathrm {Sel}}(\psi )$
to the size of
![]() $\operatorname {\mathrm {Sel}}(\widehat \psi )$
, where
$\operatorname {\mathrm {Sel}}(\widehat \psi )$
, where
![]() $\widehat \psi \colon \widehat Y \to \widehat X$
is the dual isogeny. Applied to the isogeny
$\widehat \psi \colon \widehat Y \to \widehat X$
is the dual isogeny. Applied to the isogeny
![]() $\phi _d \colon A_d \to B_d$
, it reads
$\phi _d \colon A_d \to B_d$
, it reads
 $$ \begin{align} c(\phi_d) = \dfrac{\#\operatorname{\mathrm{Sel}}(\phi_d)}{\#\operatorname{\mathrm{Sel}}(\widehat\phi_d)} \cdot \dfrac{\#\widehat B_d[\widehat\phi_d]({\mathbb Q})}{\# A_d[\phi_d]({\mathbb Q})}. \end{align} $$
$$ \begin{align} c(\phi_d) = \dfrac{\#\operatorname{\mathrm{Sel}}(\phi_d)}{\#\operatorname{\mathrm{Sel}}(\widehat\phi_d)} \cdot \dfrac{\#\widehat B_d[\widehat\phi_d]({\mathbb Q})}{\# A_d[\phi_d]({\mathbb Q})}. \end{align} $$
Proof of Theorem 2.4.
First note that if A is any abelian variety and
![]() $p>2$
, then
$p>2$
, then
![]() $A_d[p]({\mathbb Q}) = 0$
for all but finitely many quadratic twists of A. Indeed, if
$A_d[p]({\mathbb Q}) = 0$
for all but finitely many quadratic twists of A. Indeed, if
![]() $0 \neq P \in A_d[p]({\mathbb Q})$
, then the Galois module
$0 \neq P \in A_d[p]({\mathbb Q})$
, then the Galois module
![]() $A[p]$
has a subrepresentation isomorphic to the quadratic character
$A[p]$
has a subrepresentation isomorphic to the quadratic character
![]() $\chi _d \colon \operatorname {\mathrm {Gal}}(\overline {\mathbb Q}/{\mathbb Q}) \to \mathbb F_p^{\times }$
that cuts out the extension
$\chi _d \colon \operatorname {\mathrm {Gal}}(\overline {\mathbb Q}/{\mathbb Q}) \to \mathbb F_p^{\times }$
that cuts out the extension
![]() ${\mathbb Q}(\sqrt d)/{\mathbb Q}$
. Since
${\mathbb Q}(\sqrt d)/{\mathbb Q}$
. Since
![]() $A[p]$
is finite-dimensional, there can only be finitely many such d. As a consequence, if
$A[p]$
is finite-dimensional, there can only be finitely many such d. As a consequence, if
![]() $\phi :A\to B$
is a p-isogeny, then
$\phi :A\to B$
is a p-isogeny, then
![]() $A[\phi ]\subset A[p]$
, and we see that
$A[\phi ]\subset A[p]$
, and we see that
![]() $A_d[\phi _d]({\mathbb Q}) = 0$
for all but finitely many d.
$A_d[\phi _d]({\mathbb Q}) = 0$
for all but finitely many d.
We may therefore ignore the finitely many
![]() $d\in \Sigma ^+$
such that
$d\in \Sigma ^+$
such that
![]() $\#A_d[\phi _d]({\mathbb Q})\#\widehat B_d[\widehat \phi _d]({\mathbb Q}) \ne 1$
. Hence, from (2.1), we have
$\#A_d[\phi _d]({\mathbb Q})\#\widehat B_d[\widehat \phi _d]({\mathbb Q}) \ne 1$
. Hence, from (2.1), we have
Now, if
![]() $d\in \Sigma ^+$
, then
$d\in \Sigma ^+$
, then
![]() $\phi _d = \phi $
over
$\phi _d = \phi $
over
![]() ${\mathbb Q}_{\ell }$
, for all primes
${\mathbb Q}_{\ell }$
, for all primes
![]() $\ell \mid pN\infty $
. Hence, by Lemma 2.5, we have
$\ell \mid pN\infty $
. Hence, by Lemma 2.5, we have
![]() $c(\phi _d) = c(\phi ) =p^i$
for all
$c(\phi _d) = c(\phi ) =p^i$
for all
![]() $d\in \Sigma ^+$
. It follows that
$d\in \Sigma ^+$
. It follows that
for all but finitely many
![]() $d\in \Sigma ^+$
.
$d\in \Sigma ^+$
.
Finally, we note that for all but finitely many
![]() $d\in \Sigma ^+$
, the inclusion
$d\in \Sigma ^+$
, the inclusion
![]() $A_d[\phi _d]\to A_d[p]$
induces an injection
$A_d[\phi _d]\to A_d[p]$
induces an injection
Indeed, by [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS19, (9.1)], the kernel of this map is
![]() $B_d[\psi _d]({\mathbb Q})/\phi _d(A_d[p]({\mathbb Q}))$
, where
$B_d[\psi _d]({\mathbb Q})/\phi _d(A_d[p]({\mathbb Q}))$
, where
![]() $\psi _d \colon B_d \to A_d$
is the isogeny such that
$\psi _d \colon B_d \to A_d$
is the isogeny such that
![]() $\psi _d \circ \phi _d = [p]$
. As before, this kernel vanishes for all but finitely many d. Hence, for such d, we have
$\psi _d \circ \phi _d = [p]$
. As before, this kernel vanishes for all but finitely many d. Hence, for such d, we have
![]() $\dim _{\mathbb F_p}\operatorname {\mathrm {Sel}}_p(A_d)\ge i$
, and the exact sequence
$\dim _{\mathbb F_p}\operatorname {\mathrm {Sel}}_p(A_d)\ge i$
, and the exact sequence
implies that
.
3 Quotients of
 $J_0(N)$
with a
$J_0(N)$
with a
 $p$
-isogeny
$p$
-isogeny
For
![]() $N \geq 1$
, let
$N \geq 1$
, let
![]() $J_0(N)$
be the Jacobian of the modular curve
$J_0(N)$
be the Jacobian of the modular curve
![]() $X_0(N)$
over
$X_0(N)$
over
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Theorem 3.1. Let A be a simple abelian variety over
![]() ${\mathbb Q}$
arising as a quotient of
${\mathbb Q}$
arising as a quotient of
![]() $J_0(N)$
for some integer
$J_0(N)$
for some integer
![]() $N\ge 1$
. Assume that A admits a degree p isogeny
$N\ge 1$
. Assume that A admits a degree p isogeny
![]() $\phi \colon A \to B$
over
$\phi \colon A \to B$
over
![]() ${\mathbb Q}$
for some prime
${\mathbb Q}$
for some prime
![]() $p \geq 3$
and that
$p \geq 3$
and that
![]() $c(\phi ) \geq p^2$
. Then
$c(\phi ) \geq p^2$
. Then
Proof. Let
![]() $M\mid N$
be the minimal positive integer such that A is a quotient of
$M\mid N$
be the minimal positive integer such that A is a quotient of
![]() $J_0(M)$
. Then there is a newform
$J_0(M)$
. Then there is a newform
![]() $f = \sum a_nq^n\in S_2(\Gamma _0(M))$
such that the coefficient field
$f = \sum a_nq^n\in S_2(\Gamma _0(M))$
such that the coefficient field
![]() $E := {\mathbb Q}(\{a_n\})$
is isomorphic to
$E := {\mathbb Q}(\{a_n\})$
is isomorphic to
![]() $\operatorname {\mathrm {End}}_{\mathbb Q}(A) \otimes {\mathbb Q}$
and
$\operatorname {\mathrm {End}}_{\mathbb Q}(A) \otimes {\mathbb Q}$
and
![]() $L(A, s) = \prod _{\sigma \in \operatorname {\mathrm {Hom}}(E,\mathbb C)} L(f^{\sigma },s)$
. Since
$L(A, s) = \prod _{\sigma \in \operatorname {\mathrm {Hom}}(E,\mathbb C)} L(f^{\sigma },s)$
. Since
![]() $J_0(M)$
has good reduction at all primes
$J_0(M)$
has good reduction at all primes
![]() $\ell \nmid M$
, so does A.
$\ell \nmid M$
, so does A.
Let
![]() $\Sigma $
be the set of squarefree integers d such that
$\Sigma $
be the set of squarefree integers d such that
![]() $d\in {\mathbb Z}_{\ell }^{\times 2}$
for all primes
$d\in {\mathbb Z}_{\ell }^{\times 2}$
for all primes
![]() $\ell \mid pM$
. By [Reference Ono and SkinnerOS98, Corollary 3], we have
$\ell \mid pM$
. By [Reference Ono and SkinnerOS98, Corollary 3], we have
where
![]() $f_d$
is the dth quadratic twist of f. Moreover, by [Reference KatoKat04, Corollary 14.3], or alternatively by [Reference Gross and ZagierGZ86, Reference Kolyvagin and LogachëvKL89] and [Reference Bump, Friedberg and HoffsteinBFH90, Theorem 1], we have
$f_d$
is the dth quadratic twist of f. Moreover, by [Reference KatoKat04, Corollary 14.3], or alternatively by [Reference Gross and ZagierGZ86, Reference Kolyvagin and LogachëvKL89] and [Reference Bump, Friedberg and HoffsteinBFH90, Theorem 1], we have
![]() $\operatorname {\mathrm {rk}} A_d({\mathbb Q}) = 0$
whenever
$\operatorname {\mathrm {rk}} A_d({\mathbb Q}) = 0$
whenever
![]() $L( f_d,1) \ne 0$
.
$L( f_d,1) \ne 0$
.
By Lemma 2.5 and the assumption that
![]() $d\in {\mathbb Z}_{\ell }^{\times 2}$
for all primes
$d\in {\mathbb Z}_{\ell }^{\times 2}$
for all primes
![]() $\ell \mid pM$
, we have
$\ell \mid pM$
, we have
![]() $c_{\ell }(\phi _d) = c_{\ell }(\phi )$
for all finite primes
$c_{\ell }(\phi _d) = c_{\ell }(\phi )$
for all finite primes
![]() $\ell $
and all
$\ell $
and all
![]() $d \in \Sigma $
. If
$d \in \Sigma $
. If
![]() $d>0$
, we therefore have
$d>0$
, we therefore have
![]() $c(\phi _d) = c(\phi ) \geq p^2$
. If
$c(\phi _d) = c(\phi ) \geq p^2$
. If
![]() $d< 0$
, we have
$d< 0$
, we have
![]() $c_{\infty }(\phi _d)/c_{\infty }(\phi ) \in \{p, p^{-1}\}$
by Lemma 2.6, so
$c_{\infty }(\phi _d)/c_{\infty }(\phi ) \in \{p, p^{-1}\}$
by Lemma 2.6, so
![]() $c(\phi _d) \geq c(\phi )/p \geq p$
. Thus, we have
$c(\phi _d) \geq c(\phi )/p \geq p$
. Thus, we have
![]() $c(\phi _d) \geq p$
for all
$c(\phi _d) \geq p$
for all
![]() $d \in \Sigma $
. Applying Theorem 2.4 both to A and to
$d \in \Sigma $
. Applying Theorem 2.4 both to A and to
![]() $A_{-1}$
, we have
$A_{-1}$
, we have
for all but finitely many
![]() $d\in \Sigma $
. It follows that
$d\in \Sigma $
. It follows that
as desired.
4 Quotients of
 $J_0(N)$
with
$J_0(N)$
with
 $N$
prime
$N$
prime
Let N be a prime, and let
![]() $p \geq 3$
be a divisor of
$p \geq 3$
be a divisor of
![]() $\frac {N-1}{\mathrm {gcd}(12,N-1)}$
. Let
$\frac {N-1}{\mathrm {gcd}(12,N-1)}$
. Let
![]() $\mathbb T$
be the finite
$\mathbb T$
be the finite
![]() ${\mathbb Z}$
-algebra generated by the Hecke operators acting on the space
${\mathbb Z}$
-algebra generated by the Hecke operators acting on the space
![]() $S_2(\Gamma _0(N))$
of weight
$S_2(\Gamma _0(N))$
of weight
![]() $2$
cusp forms on
$2$
cusp forms on
![]() $\Gamma _0(N)$
. For each newform
$\Gamma _0(N)$
. For each newform
![]() $f\in S_2(\Gamma _0(N))$
, let
$f\in S_2(\Gamma _0(N))$
, let
![]() $\lambda _f \colon \mathbb T\to \mathbb C$
be the homomorphism giving the action of the Hecke operators on f, and let
$\lambda _f \colon \mathbb T\to \mathbb C$
be the homomorphism giving the action of the Hecke operators on f, and let
![]() $I_f=\ker \lambda _f$
. Let
$I_f=\ker \lambda _f$
. Let
![]() $J = J_0(N)$
be the modular Jacobian. Then
$J = J_0(N)$
be the modular Jacobian. Then
![]() $\mathbb T \hookrightarrow \operatorname {\mathrm {End}}_{\mathbb Q} J$
, and
$\mathbb T \hookrightarrow \operatorname {\mathrm {End}}_{\mathbb Q} J$
, and
![]() $A_f := J/I_fJ$
is an abelian variety over
$A_f := J/I_fJ$
is an abelian variety over
![]() ${\mathbb Q}$
called the optimal quotient corresponding to f [Reference EmertonEme03].
${\mathbb Q}$
called the optimal quotient corresponding to f [Reference EmertonEme03].
By [Reference MazurMaz77, Theorem 1], the torsion subgroup
![]() $J_0(N)({\mathbb Q})_{\mathrm {tors}}$
is cyclic of order
$J_0(N)({\mathbb Q})_{\mathrm {tors}}$
is cyclic of order
![]() $\frac {N-1}{\gcd (12,N-1)}$
and hence is divisible by p. By [Reference EmertonEme03, Theorem B], there exists at least one optimal quotient
$\frac {N-1}{\gcd (12,N-1)}$
and hence is divisible by p. By [Reference EmertonEme03, Theorem B], there exists at least one optimal quotient
![]() $A = A_f$
with a point
$A = A_f$
with a point
![]() $P \in A({\mathbb Q})$
of order p. Let
$P \in A({\mathbb Q})$
of order p. Let
![]() $B = A/\langle P\rangle $
be the quotient, let
$B = A/\langle P\rangle $
be the quotient, let
![]() $\phi :A\to B$
be the canonical p-isogeny over
$\phi :A\to B$
be the canonical p-isogeny over
![]() ${\mathbb Q}$
, and let
${\mathbb Q}$
, and let
![]() $\widehat \phi :\widehat B\to \widehat A$
be the dual isogeny.
$\widehat \phi :\widehat B\to \widehat A$
be the dual isogeny.
Proof of Theorem 1.2.
By Theorem 3.1, it is enough to prove that
![]() $c(\widehat \phi ) = p^2$
. By the Greenberg–Wiles formula in equation (2.1), it is equivalent to show that
$c(\widehat \phi ) = p^2$
. By the Greenberg–Wiles formula in equation (2.1), it is equivalent to show that
![]() $c(\phi ) = p^{-2}$
. By Lemma 2.5, we have
$c(\phi ) = p^{-2}$
. By Lemma 2.5, we have
![]() $c_{\ell }(\phi ) = 1$
whenever
$c_{\ell }(\phi ) = 1$
whenever
![]() $\ell \notin \{p, N, \infty \}$
. Moreover, by Lemma 2.6, we have
$\ell \notin \{p, N, \infty \}$
. Moreover, by Lemma 2.6, we have
![]() $c_{\infty }(\phi ) = \#\ker (\phi )(\mathbb R)^{-1} = p^{-1}$
. To compute the remaining two local Selmer ratios, we use some facts about the Néron model of A.
$c_{\infty }(\phi ) = \#\ker (\phi )(\mathbb R)^{-1} = p^{-1}$
. To compute the remaining two local Selmer ratios, we use some facts about the Néron model of A.
Lemma 4.1. We have
![]() $c_p(\phi ) = 1$
.
$c_p(\phi ) = 1$
.
Proof. Since A has good reduction at p, we have
![]() $c_p(A) = c_p(B) = 1$
. In the notation of Lemma 2.3, we therefore have
$c_p(A) = c_p(B) = 1$
. In the notation of Lemma 2.3, we therefore have
![]() $c_p(\phi ) = \gamma _{\phi , p}$
. Now, the generator P of
$c_p(\phi ) = \gamma _{\phi , p}$
. Now, the generator P of
![]() $\ker (\phi )$
is the image of a rational cuspidal divisor under the map
$\ker (\phi )$
is the image of a rational cuspidal divisor under the map
![]() $J_0(N) \to A$
by [Reference EmertonEme03, Theorem B]. Thus, by [Reference MazurMaz77, II.11.11],
$J_0(N) \to A$
by [Reference EmertonEme03, Theorem B]. Thus, by [Reference MazurMaz77, II.11.11],
![]() $\phi $
extends to an étale isogeny of Néron models over
$\phi $
extends to an étale isogeny of Néron models over
![]() ${\mathbb Z}_p$
. It follows that
${\mathbb Z}_p$
. It follows that
![]() $\mathrm {Lie}(\mathcal {A}) \to \mathrm {Lie}(\mathcal {B})$
is an isomorphism and
$\mathrm {Lie}(\mathcal {A}) \to \mathrm {Lie}(\mathcal {B})$
is an isomorphism and
![]() $\gamma _{\phi , p}=1$
.
$\gamma _{\phi , p}=1$
.
Lemma 4.2. We have
![]() $c_N(\phi ) = p^{-1}$
.
$c_N(\phi ) = p^{-1}$
.
Proof. The Atkin–Lehner operator
![]() $W_N$
acts on A by
$W_N$
acts on A by
![]() $-1$
. Indeed, A belongs to the Eisenstein quotient of
$-1$
. Indeed, A belongs to the Eisenstein quotient of
![]() $J = J_0(N)$
, which is itself a quotient of
$J = J_0(N)$
, which is itself a quotient of
![]() $J^-$
, the maximal quotient of J on which the Atkin–Lehner eigenvalue is
$J^-$
, the maximal quotient of J on which the Atkin–Lehner eigenvalue is
![]() $-1$
[Reference MazurMaz77, Proposition 17.10]. Hence, the global root number of f is
$-1$
[Reference MazurMaz77, Proposition 17.10]. Hence, the global root number of f is
![]() $+1$
, and by [Reference Conrad and SteinCS01, Proposition 7.1], the abelian variety
$+1$
, and by [Reference Conrad and SteinCS01, Proposition 7.1], the abelian variety
![]() $A = A_f$
has split purely toric reduction. Moreover, the order p point P reduces to a non-identity component of the special fibre of the Néron model of A over
$A = A_f$
has split purely toric reduction. Moreover, the order p point P reduces to a non-identity component of the special fibre of the Néron model of A over
![]() ${\mathbb Z}_N$
, since specialisation induces an isomorphism from
${\mathbb Z}_N$
, since specialisation induces an isomorphism from
![]() $A({\mathbb Q})_{\mathrm {tors}}$
to the component group
$A({\mathbb Q})_{\mathrm {tors}}$
to the component group
![]() $\Phi _A$
by [Reference EmertonEme03, Theorem B]. Thus, the lemma follows from [Reference Bruin, Flynn and ShnidmanBFS21, Proposition 5.1].
$\Phi _A$
by [Reference EmertonEme03, Theorem B]. Thus, the lemma follows from [Reference Bruin, Flynn and ShnidmanBFS21, Proposition 5.1].
We compute
![]() $c(\phi ) = \prod _{\ell \leq \infty }c_{\ell }(\phi ) = c_N(\phi )c_{\infty }(\phi ) = p^{-2}$
, as desired.
$c(\phi ) = \prod _{\ell \leq \infty }c_{\ell }(\phi ) = c_N(\phi )c_{\infty }(\phi ) = p^{-2}$
, as desired.
5 Applications to elliptic curves
Proof of Theorem 1.3.
By a recent result of Smith [Reference SmithSmi20, Corollary 1.4], we have
under the assumption that either
![]() $E[2]({\mathbb Q}) = 0$
or
$E[2]({\mathbb Q}) = 0$
or
![]() $E[2]({\mathbb Q}) = ({\mathbb Z}/2{\mathbb Z})^2$
and E does not admit a cyclic
$E[2]({\mathbb Q}) = ({\mathbb Z}/2{\mathbb Z})^2$
and E does not admit a cyclic
![]() $4$
-isogeny. In our case, E also admits a p-isogeny. If
$4$
-isogeny. In our case, E also admits a p-isogeny. If
![]() $E[2]({\mathbb Q}) = ({\mathbb Z}/2{\mathbb Z})^2$
, then E cannot also admit a cyclic
$E[2]({\mathbb Q}) = ({\mathbb Z}/2{\mathbb Z})^2$
, then E cannot also admit a cyclic
![]() $4$
-isogeny: otherwise, the isogeny class of E would contain a cyclic
$4$
-isogeny: otherwise, the isogeny class of E would contain a cyclic
![]() $8p$
-isogeny, but
$8p$
-isogeny, but
![]() $Y_0(8p)({\mathbb Q}) = \emptyset $
for
$Y_0(8p)({\mathbb Q}) = \emptyset $
for
![]() $p \geq 3$
[Reference KenkuKen82, Theorem 1]. Thus, E satisfies the hypotheses of Smith’s result, and by Theorem 2.4 and our assumption that
$p \geq 3$
[Reference KenkuKen82, Theorem 1]. Thus, E satisfies the hypotheses of Smith’s result, and by Theorem 2.4 and our assumption that
![]() $c(\phi )\ge p^2$
, it follows that
$c(\phi )\ge p^2$
, it follows that
![]() for
for
![]() $100\%$
of
$100\%$
of
![]() $d\in \Sigma ^+$
.
$d\in \Sigma ^+$
.
It is natural to ask about the scope of Theorem 1.3. In this direction, we have:
Proposition 5.1. Suppose that
![]() $p> 2$
and that
$p> 2$
and that
![]() $\phi \colon E \to E'$
is a p-isogeny of elliptic curves over
$\phi \colon E \to E'$
is a p-isogeny of elliptic curves over
![]() ${\mathbb Q}$
. Suppose also that E has at least three primes, distinct from p, of multiplicative reduction. Then there exists an integer d such that either
${\mathbb Q}$
. Suppose also that E has at least three primes, distinct from p, of multiplicative reduction. Then there exists an integer d such that either
![]() $c(\phi _d) \geq p^2$
or
$c(\phi _d) \geq p^2$
or
![]() $c(\widehat \phi _d) \geq p^2$
. In particular, the conclusion of Theorem 1.3 applies to at least one of E or
$c(\widehat \phi _d) \geq p^2$
. In particular, the conclusion of Theorem 1.3 applies to at least one of E or
![]() $E'$
.
$E'$
.
Proof. We apply [Reference Dokchitser and DokchitserDD15, Table 1]. Let
![]() $\ell _1, \ell _2, \ell _3$
be the primes of multiplicative reduction, and write
$\ell _1, \ell _2, \ell _3$
be the primes of multiplicative reduction, and write
![]() $v_i$
for the corresponding
$v_i$
for the corresponding
![]() $\ell _i$
-adic valuation. Let
$\ell _i$
-adic valuation. Let
![]() $j, j'$
be the j-invariants of E and
$j, j'$
be the j-invariants of E and
![]() $E'$
. Replacing
$E'$
. Replacing
![]() $E, E'$
by quadratic twists, we may assume that all three primes have split multiplicative reduction. Moreover, we may further twist so that, at every other prime, E has either good or additive reduction.
$E, E'$
by quadratic twists, we may assume that all three primes have split multiplicative reduction. Moreover, we may further twist so that, at every other prime, E has either good or additive reduction.
After reordering and possibly replacing
![]() $\phi $
with its dual, we may assume that
$\phi $
with its dual, we may assume that
![]() $v_i(j) = pv_i(j')$
for
$v_i(j) = pv_i(j')$
for
![]() $i = 1,2$
. Indeed, for each i, we have either
$i = 1,2$
. Indeed, for each i, we have either
![]() $v_i(j) = pv_i(j')$
or
$v_i(j) = pv_i(j')$
or
![]() $v_i(j') = pv_i(j)$
, so, possibly replacing
$v_i(j') = pv_i(j)$
, so, possibly replacing
![]() $\phi $
with its dual, the first option must happen for at least two primes.
$\phi $
with its dual, the first option must happen for at least two primes.
Twisting again by an integer d, such that
![]() $\ell _3\mid d$
and
$\ell _3\mid d$
and
![]() $\left (\frac {d}{p}\right ) = 1$
for all other primes of bad reduction, we may assume that
$\left (\frac {d}{p}\right ) = 1$
for all other primes of bad reduction, we may assume that
![]() $E, E'$
have additive, potentially multiplicative reduction at
$E, E'$
have additive, potentially multiplicative reduction at
![]() $\ell _3$
. Similarly, we may assume that
$\ell _3$
. Similarly, we may assume that
![]() $E[\phi ](\mathbb R) = 0$
. Hence, by [Reference Dokchitser and DokchitserDD15, Table 1] and Lemma 2.3, we have
$E[\phi ](\mathbb R) = 0$
. Hence, by [Reference Dokchitser and DokchitserDD15, Table 1] and Lemma 2.3, we have
![]() $c_{\ell _i}(\phi ) = p$
for
$c_{\ell _i}(\phi ) = p$
for
![]() $i = 1,2$
and
$i = 1,2$
and
![]() $c_{\ell _3}(\phi )=1$
. Moreover, as in Lemma 2.6, we have
$c_{\ell _3}(\phi )=1$
. Moreover, as in Lemma 2.6, we have
![]() $c_{\infty }(\phi ) = 1$
.
$c_{\infty }(\phi ) = 1$
.
Twisting at p so that E has additive reduction, we have either
![]() $c_{p}(\phi ) = 1$
or p, again by [Reference Dokchitser and DokchitserDD15, Table 1]. Finally, by construction, A has good or additive reduction at all the other primes, so
$c_{p}(\phi ) = 1$
or p, again by [Reference Dokchitser and DokchitserDD15, Table 1]. Finally, by construction, A has good or additive reduction at all the other primes, so
![]() $c_{\ell }(\phi ) = 1$
for all primes
$c_{\ell }(\phi ) = 1$
for all primes
![]() $\ell \nmid \ell _1\ell _2\ell _3p\infty $
[Reference Dokchitser and DokchitserDD15, Table 1]. Putting everything together, we have
$\ell \nmid \ell _1\ell _2\ell _3p\infty $
[Reference Dokchitser and DokchitserDD15, Table 1]. Putting everything together, we have
![]() $c(\phi ) \ge p^2$
.
$c(\phi ) \ge p^2$
.
Proposition 5.1 shows that in a certain natural sense, Theorem 1.3 applies to ‘most’ twist families of elliptic curves
![]() $E/{\mathbb Q}$
with an isogeny of degree
$E/{\mathbb Q}$
with an isogeny of degree
![]() $p> 2$
. To make this claim more precise, we first recall that for
$p> 2$
. To make this claim more precise, we first recall that for
![]() $p \notin \{3,5,7,13\}$
, there are only finitely many j-invariants of elliptic curves with a p-isogeny [Reference MazurMaz78]. The modular curves
$p \notin \{3,5,7,13\}$
, there are only finitely many j-invariants of elliptic curves with a p-isogeny [Reference MazurMaz78]. The modular curves
![]() $X_0(p)$
with
$X_0(p)$
with
![]() $p \in \{3,5,7,13\}$
are all isomorphic to
$p \in \{3,5,7,13\}$
are all isomorphic to
![]() ${\mathbb P}^1$
. Hence, there are infinitely many j-invariants of such elliptic curves over
${\mathbb P}^1$
. Hence, there are infinitely many j-invariants of such elliptic curves over
![]() ${\mathbb Q}$
. However, for any p in this set, and for any
${\mathbb Q}$
. However, for any p in this set, and for any
![]() $k \geq 1$
, one can show that
$k \geq 1$
, one can show that
![]() $100\%$
of rational points in
$100\%$
of rational points in
![]() $X_0(p)({\mathbb Q})$
, ordered by height, have at least k primes of potentially multiplicative reduction. We will not prove this here, but for arguments along these lines, see [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21].
$X_0(p)({\mathbb Q})$
, ordered by height, have at least k primes of potentially multiplicative reduction. We will not prove this here, but for arguments along these lines, see [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21].
6 An example: an elliptic curve with a
 $5$
-isogeny
$5$
-isogeny
In this final section, we look at the example
![]() $N = 11$
and
$N = 11$
and
![]() $p = 5$
. In this case,
$p = 5$
. In this case,
![]() $J_0(11)$
is an elliptic curve with a
$J_0(11)$
is an elliptic curve with a
![]() $5$
-isogeny
$5$
-isogeny
![]() $\phi \colon J_0(11) \to E$
, and we work out an explicit lower bound on the proportion of squarefree integers d with
$\phi \colon J_0(11) \to E$
, and we work out an explicit lower bound on the proportion of squarefree integers d with
![]() .
.
In [Reference DelaunayDel01], Delaunay gives a Cohen–Lenstra type heuristic, which predicts that, for fixed
![]() $r \in \{0,1\}$
, and as E varies over all elliptic curves over
$r \in \{0,1\}$
, and as E varies over all elliptic curves over
![]() ${\mathbb Q}$
ordered by conductor,
${\mathbb Q}$
ordered by conductor,

Assuming Goldfeld’s conjecture that
![]() $50\%$
of elliptic curves have rank
$50\%$
of elliptic curves have rank
![]() $0$
and
$0$
and
![]() $50\%$
have rank
$50\%$
have rank
![]() $1$
, this distribution predicts that
$1$
, this distribution predicts that

Delaunay’s heuristics were presented for the family of all elliptic curves over
![]() ${\mathbb Q}$
; however, it is natural to guess that they should hold in quadratic twist families as well, as is suggested by Delaunay [Reference DelaunayDel07, Section 4] and Poonen–Rains [Reference Poonen and RainsPR12, Remark 1.9].
${\mathbb Q}$
; however, it is natural to guess that they should hold in quadratic twist families as well, as is suggested by Delaunay [Reference DelaunayDel07, Section 4] and Poonen–Rains [Reference Poonen and RainsPR12, Remark 1.9].
In the following example, we prove that the family of quadratic twists of E do not follow this distribution. In particular, in twist families of elliptic curves with a p-isogeny, our example shows that the distribution of the groups
![]() must follow a different distribution.
must follow a different distribution.
Theorem 6.1. Let
![]() $E \colon y^2 + y = x^3 - x^2 - 7820x - 263580$
, an elliptic curve of conductor
$E \colon y^2 + y = x^3 - x^2 - 7820x - 263580$
, an elliptic curve of conductor
![]() $11$
. Then at least
$11$
. Then at least
![]() $11/48 \approx 22.9\%$
of squarefree integers d satisfy
$11/48 \approx 22.9\%$
of squarefree integers d satisfy
![]() .
.
Proof. The modular curve
![]() $X_0(11)$
is genus 1 and has model
$X_0(11)$
is genus 1 and has model
![]() $E' \colon y^2 + y = x^3 - x^2 - 10x - 20$
. We therefore have
$E' \colon y^2 + y = x^3 - x^2 - 10x - 20$
. We therefore have
![]() $E' \simeq J_0(11) \simeq A_f$
, where f is the unique weight two eigenform of level
$E' \simeq J_0(11) \simeq A_f$
, where f is the unique weight two eigenform of level
![]() $\Gamma _0(11)$
. The torsion subgroup is order
$\Gamma _0(11)$
. The torsion subgroup is order
![]() $5$
generated by the point
$5$
generated by the point
![]() $(5,5)$
. The curve E in the theorem is the quotient
$(5,5)$
. The curve E in the theorem is the quotient
![]() $\phi \colon E' \to E$
by the subgroup generated by
$\phi \colon E' \to E$
by the subgroup generated by
![]() $(5,5)$
.
$(5,5)$
.
Since
![]() $E[2]({\mathbb Q}) = 0$
, by [Reference SmithSmi20, Corollary 1.4], we have
$E[2]({\mathbb Q}) = 0$
, by [Reference SmithSmi20, Corollary 1.4], we have
![]() $\operatorname {\mathrm {rk}} E_d({\mathbb Q}) \le 1$
for
$\operatorname {\mathrm {rk}} E_d({\mathbb Q}) \le 1$
for
![]() $100\%$
of squarefree integers d. Hence, by Theorem 2.4,
$100\%$
of squarefree integers d. Hence, by Theorem 2.4,
![]() whenever
whenever
![]() $c(\widehat \phi ) \ge 5^2$
or, equivalently, whenever
$c(\widehat \phi ) \ge 5^2$
or, equivalently, whenever
![]() $c(\phi ) \le 5^{-2}$
.
$c(\phi ) \le 5^{-2}$
.
By Lemmas 2.6, 4.1 and 4.2, or by [Reference Dokchitser and DokchitserDD15, Table 1], we have
![]() $c_{11}(\phi ) = \frac 15$
,
$c_{11}(\phi ) = \frac 15$
,
![]() $c_{\infty }(\phi ) = \frac 15$
and
$c_{\infty }(\phi ) = \frac 15$
and
![]() $c_5(\phi ) = 1$
. Moreover, by [Reference Dokchitser and DokchitserDD15, Table 1], we have
$c_5(\phi ) = 1$
. Moreover, by [Reference Dokchitser and DokchitserDD15, Table 1], we have
![]() $c_5(\phi _d) = 1$
for all d. If
$c_5(\phi _d) = 1$
for all d. If
![]() $\ell \nmid 5\cdot 11\cdot \infty $
, we have
$\ell \nmid 5\cdot 11\cdot \infty $
, we have
![]() $c_{\ell }(\phi _d) = 1$
by Lemma 2.5. Hence, if
$c_{\ell }(\phi _d) = 1$
by Lemma 2.5. Hence, if
![]() $\Sigma ^+$
denotes the set of positive squarefree integers, such that
$\Sigma ^+$
denotes the set of positive squarefree integers, such that
![]() $d\in {\mathbb Z}_{11}^{\times 2}$
, then
$d\in {\mathbb Z}_{11}^{\times 2}$
, then
![]() $c(\phi _d) \le 5^{-2}$
for all
$c(\phi _d) \le 5^{-2}$
for all
![]() $d\in \Sigma ^+$
.
$d\in \Sigma ^+$
.
As a subset of the set of squarefree integers,
![]() $\Sigma ^+$
has relative density
$\Sigma ^+$
has relative density
Hence, at least
![]() $11/48$
of squarefree integers d satisfy
$11/48$
of squarefree integers d satisfy
![]() .
.
The fact that Delaunay’s heuristics for the distribution of the groups
![]() should be modified in certain cases was already understood in [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21], which is one reason why the authors formulate [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21, Conjecture 1] without specifying a conjectural proportion. That paper contains several results that show Delaunay’s distribution does not always hold when the (isogeny class of the) elliptic curve admits at least two independent cyclic isogenies. Theorem 1.3 shows that this phenomenon persists even in the presence of a single cyclic isogeny. It would be interesting to develop consistent heuristics that describe a conjectural distribution in all cases.
should be modified in certain cases was already understood in [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21], which is one reason why the authors formulate [Reference Bhargava, Klagsbrun, Lemke Oliver and ShnidmanBKLOS21, Conjecture 1] without specifying a conjectural proportion. That paper contains several results that show Delaunay’s distribution does not always hold when the (isogeny class of the) elliptic curve admits at least two independent cyclic isogenies. Theorem 1.3 shows that this phenomenon persists even in the presence of a single cyclic isogeny. It would be interesting to develop consistent heuristics that describe a conjectural distribution in all cases.
Acknowledgements
The authors thank Manjul Bhargava, Brendan Creutz and Robert Lemke Oliver for helpful conversations. They also thank the referees for their careful reading and helpful suggestions to improve the exposition. The first author was supported by the Israel Science Foundation (grant No. 2301/20). The second author was supported by an Emily Erskine Endowment Fund postdoctoral fellowship at The Hebrew University of Jerusalem, by the Israel Science Foundation (grant No. 1963/20) and by the Binational Science Foundation (grant No. 2018250).
Conflicts of Interest
The authors have no conflicts of interest to declare.