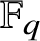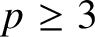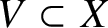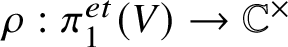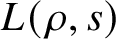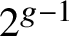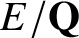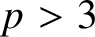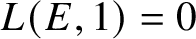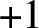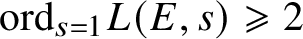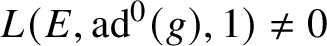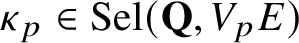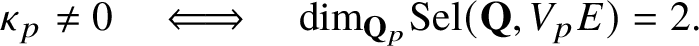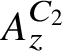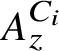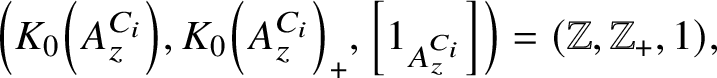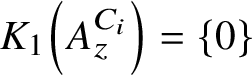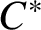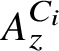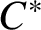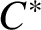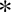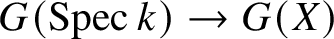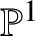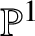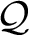Algebraic and Complex Geometry
Topological models for stable motivic invariants of regular number rings
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2022, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
p-Adic estimates of abelian Artin L-functions on curves
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Circle packings, kissing reflection groups and critically fixed anti-rational maps
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical Physics
Adiabatic theorem in the thermodynamic limit: Systems with a gap in the bulk
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gromov–Witten theory with maximal contacts
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Geometry and Geometric Analysis
Lipschitz graphs and currents in Heisenberg groups
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theoretical Computer Science
Lee–Yang zeros and the complexity of the ferromagnetic Ising model on bounded-degree graphs
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2022, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Ginzburg algebras of triangulated surfaces and perverse schobers
-
- Published online by Cambridge University Press:
- 08 February 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Stringy invariants and toric Artin stacks
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categorical traces and a relative Lefschetz–Verdier formula
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2022, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kirchhoff’s theorem for Prym varieties
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
On the nonvanishing of generalised Kato classes for elliptic curves of rank 2
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2022, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Overgroups of regular unipotent elements in reductive groups
- Part of:
-
- Published online by Cambridge University Press:
- 24 February 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Nonamenable simple
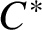 $C^*$
-algebras with tracial approximation
$C^*$
-algebras with tracial approximation
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Operator-free sparse domination
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2022, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
A symplectic look at the Fargues–Fontaine curve
-
- Published online by Cambridge University Press:
- 07 March 2022, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
Topology of random 2-dimensional cubical complexes – Erratum
-
- Published online by Cambridge University Press:
- 09 March 2022, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
C
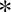 $^{\ast }$-simplicity has no local obstruction
$^{\ast }$-simplicity has no local obstruction
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Unramified logarithmic Hodge–Witt cohomology and
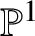 $\mathbb {P}^1$-invariance
$\mathbb {P}^1$-invariance
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational Mathematics
An operadic approach to substitution in Lie–Butcher series
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2022, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation