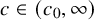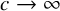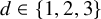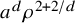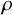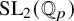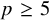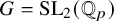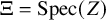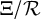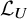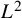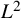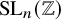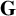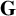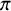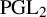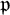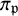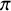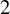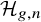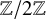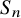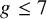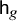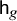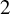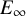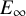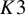Volume 12 - 2024
Differential Equations
Axisymmetric Incompressible Viscous Plasmas: Global Well-Posedness and Asymptotics
- Part of:
-
- Published online by Cambridge University Press:
- 10 September 2024, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical Physics
Pressure of a dilute spin-polarized Fermi gas: Lower bound
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2024, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Stability in the category of smooth mod-p representations of
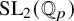 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
A proof of the Elliott–Rödl conjecture on hypertrees in Steiner triple systems
-
- Published online by Cambridge University Press:
- 06 September 2024, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical Physics
Flags of sheaves, quivers and symmetric polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2024, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
On the local
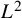 $L^2$-Bound of the Eisenstein series
$L^2$-Bound of the Eisenstein series
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2024, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Bounds on multiplicities of symmetric pairs of finite groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2024, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Persistent transcendental Bézout theorems
-
- Published online by Cambridge University Press:
- 27 August 2024, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
L-invariants for cohomological representations of PGL(2) over arbitrary number fields
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational Mathematics
Sums of squares, Hankel index and almost real rank
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Globally F-regular type of the moduli spaces of parabolic symplectic/orthogonal bundles on curves
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2024, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strict positivity of Kähler–Einstein currents
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2024, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the weight zero compactly supported cohomology of
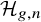 ${\mathcal {H}}_{g,n}$
${\mathcal {H}}_{g,n}$
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2024, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Orthogonality relations for deep level Deligne–Lusztig schemes of Coxeter type
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2024, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
On divisorial stability of finite covers
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2024, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic coverings of genus
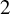 $2$ curves of Sophie Germain type
$2$ curves of Sophie Germain type
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2024, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Coble quadric
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2024, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Adams’ cobar construction as a monoidal
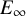 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical Physics
Quasimaps to moduli spaces of sheaves on a
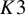 $K3$ surface
$K3$ surface
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
O’Grady tenfolds as moduli spaces of sheaves
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation