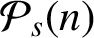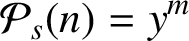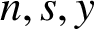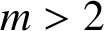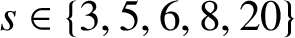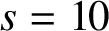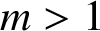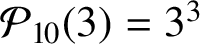THE MATHEMATICAL EXAMPLE OF GNOMONS IN ARISTOTLE, PHYSICS 3.4, 203a10–16
-
- Journal:
- The Classical Quarterly / Volume 74 / Issue 1 / May 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 67-84
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DIOPHANTINE PROBLEM CONCERNING POLYGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 345-350
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation