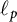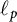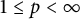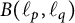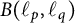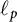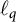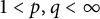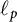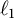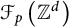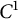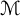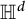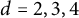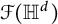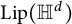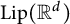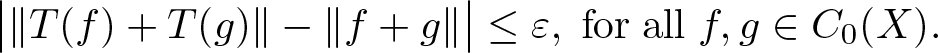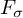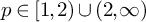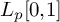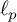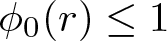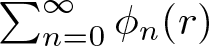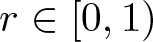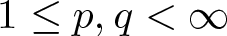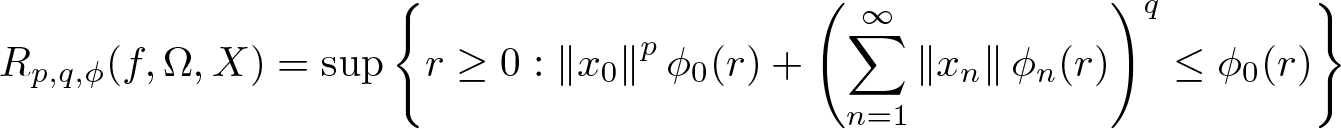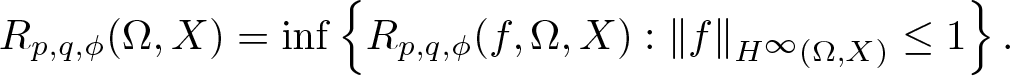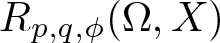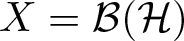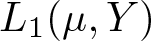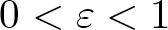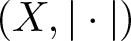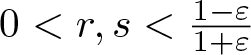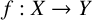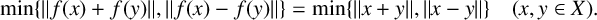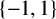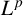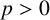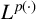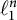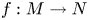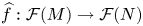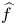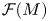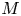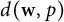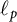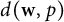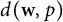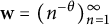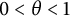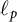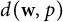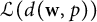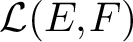158 results
Hyperbolic Metric Spaces and Stochastic Embeddings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differentiability of the operator norm on \ell _p spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
On the complete separation of unique \ell _{1} spreading models and the Lebesgue property of Banach spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Daugavet and Delta-constants of points in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
Tilings of the hyperbolic space and Lipschitz functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perturbations of norm-additive maps between continuous function spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1099-1114
-
- Article
-
- You have access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1919-1957
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
-
- You have access
- HTML
- Export citation
On weakly almost square Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 05 October 2023, pp. 979-997
-
- Article
- Export citation
ON REAL NONISOMORPHIC BANACH SPACES WITH HOMEOMORPHIC GEOMETRIC STRUCTURE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 26 July 2023, pp. 562-570
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak weight-semi-greedy Markushevich bases
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1118-1179
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
MIN-PHASE-ISOMETRIES IN STRICTLY CONVEX NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 22 March 2023, pp. 152-160
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
CONTRACTIVE SEMIGROUPS IN TOPOLOGICAL VECTOR SPACES, ON THE 100TH ANNIVERSARY OF STEFAN BANACH’S CONTRACTION PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 331-338
- Print publication:
- October 2023
-
- Article
- Export citation
BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 737-752
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Magnitude and Holmes–Thompson intrinsic volumes of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 854-867
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polish spaces of Banach spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 May 2022, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact and weakly compact Lipschitz operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1002-1020
- Print publication:
- June 2023
-
- Article
- Export citation
RETRACTED - Compact reduction in Lipschitz-free spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 08 December 2021, pp. 1683-1699
- Print publication:
- December 2021
-
- Article
- Export citation
A new complemented subspace for the Lorentz sequence spaces, with an application to its lattice of closed ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 759-769
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE EXISTENCE OF NON-NORM-ATTAINING OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 July 2021, pp. 1023-1035
- Print publication:
- May 2023
-
- Article
- Export citation