Introduction

Almost half of the Antarctic coast is bounded by ice shelves. The two largest, the Filchner–Ronne Ice Shelf (FRIS) and the Ross Ice Shelf, form a large part of the West Antarctic coast. These ice shelves drain most of West Antarctica as well as parts of East Antarctica (Reference Drewry, Jordan and JankowskiDrewry and others, 1982).

The FRIS is the second largest ice shelf in the world by area and the largest by volume. It is mainly fed by large ice streams, and drains 24% of the Antarctic ice sheet (Reference DoakeDoake, 1985). This mass transport interacts with the dynamic processes in the transition zone between the grounded ice sheet and the floating ice shelf, which play a key role in ongoing stability studies (Reference WeertmanWeertman, 1974; Reference Van der VeenVan der Veen, 1986; Reference Barcilon and MacAyealBarcilon and MacAyeal, 1993).

The water mass generated by melting and freezing processes under the FRIS, together with the High Salinity Shelf Water, create the Antarctic Bottom Water, which represents 30% of the volume of the world’s oceans (Reference FahrbachFahrbach, 1993).

To study the complex dynamic system within and underneath the ice using mass-balance calculations and numerical models, detailed knowledge of the conditions in the transition zone, especially in entrance regions of ice streams, is required. Information on the recent conditions of mass transport in the transition zone is thus essential in order to reconstruct the glacial history of the ice sheet and for prognostic studies introducing climatic variability.

Measurements

Mass-balance parameters over the southeastern Ronne Ice Shelf (RIS) were measured during the Filchner VCampaign, 1995, using different geophysical and glaciological methods (Fig. 1).

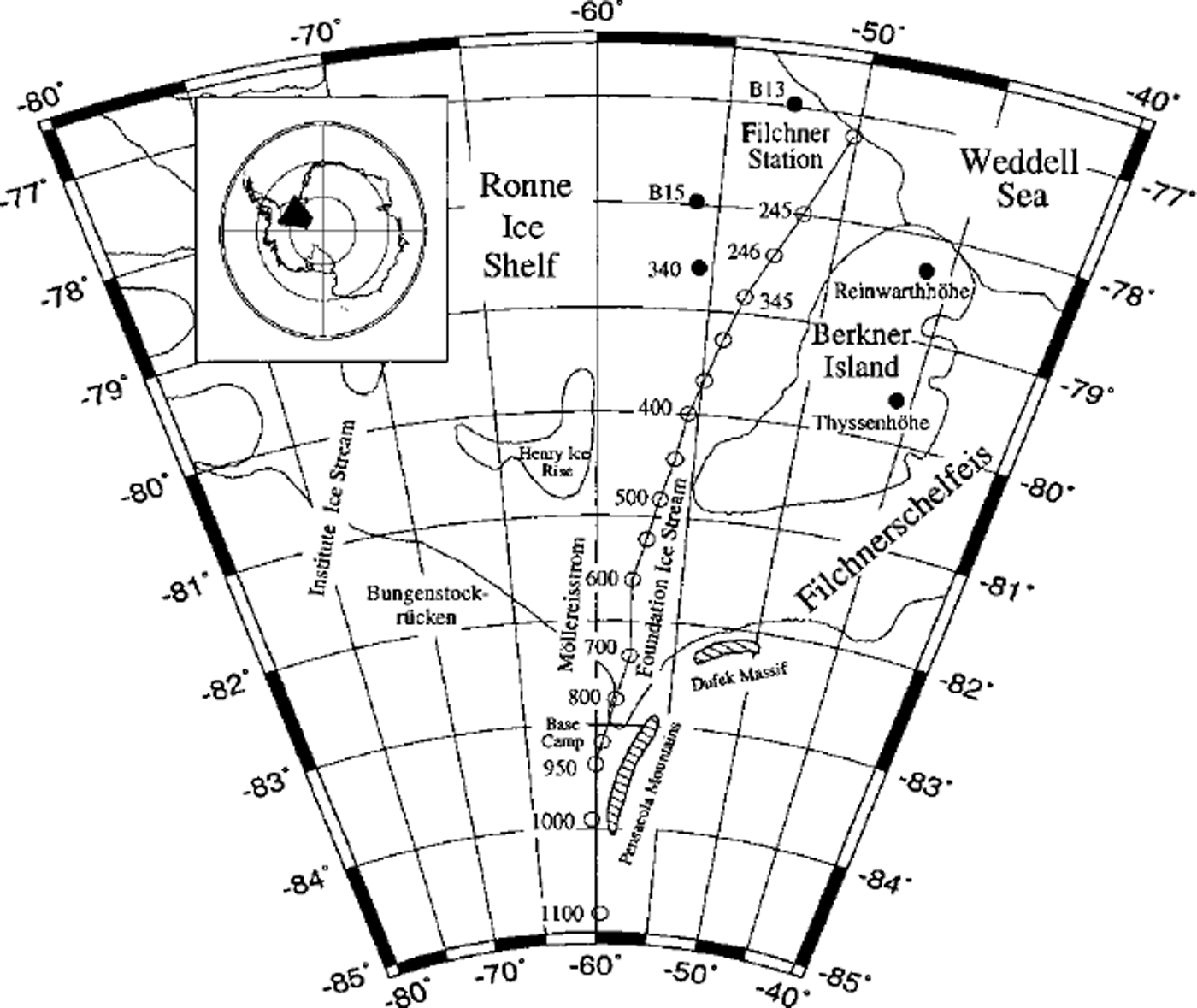
Fig. 1. Overview of the FRIS with its most prominent features. The traverse route to the grounding line of Foundation Ice Stream and the various positions referred to in the text are displayed in the map.

Airborne radio-echo sounding (RES) profiling

In total, almost 10 000 km of RES profiles (Fig. 2) were measured across the eastern RIS, using the aircraft Polar 2 as platform for the Alfred Wegener Institute’s (AWI) RES system. This system was developed in collaboration with the Technical University Hamburg–Harburg, the German Aerospace Centre (DLR) and Aerodata FlugmeBtechmk GmbH. It consists of an analogue high-frequency part, emitting bursts of 150 MHz frequency and 60 or 600 ns length, and a digital recording system. At an aircraft ground speed of 130 knots (240 km h⁻¹), the horizontal resolution is 3.25 m. The vertical resolution varies between 5 and 50 m, depending on the length of the burst (Reference NixdorfNixdorf and others, 1999).

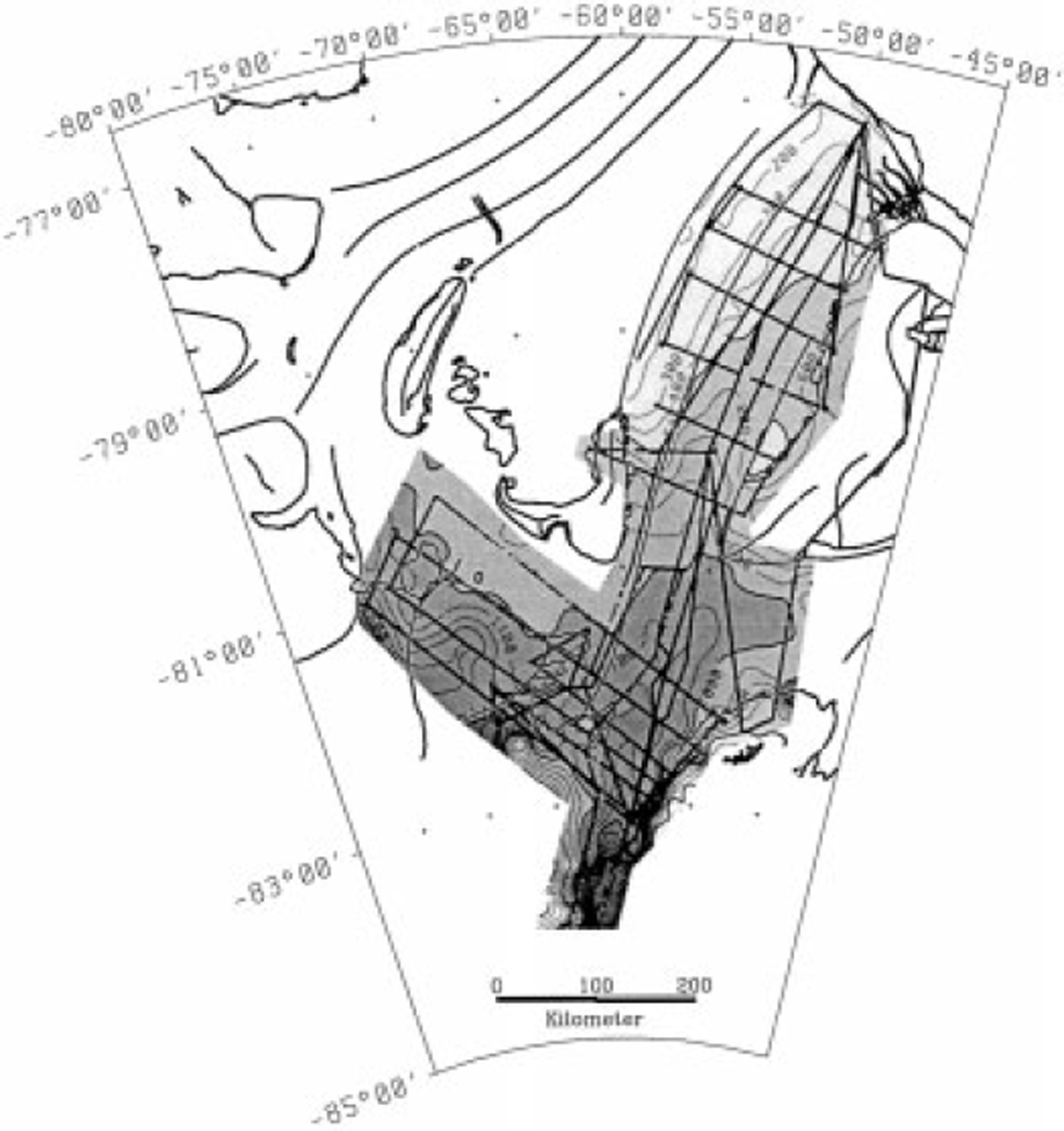
Fig. 2. Meteoric ice-thickness distribution over the eastern RIS, as deduced from airborne RES measurements. The contouring interval is 100 m; the shading interval is 1000 m. RES profiles are shown as thick lines within the shaded area.

Ice-Thickness Distribution

Processing and interpretation of the RES measurements resulted in a meteoric ice-thickness distribution for the eastern RIS, which is shown in Figure 2. For this analysis an electromagnetic wave velocity in ice of 168 m μs⁻¹ was used. The ice thickness was then corrected for the less dense firn layer by adding 10 m. These data form the basis for investigations of the mass balance in this area. In the area where Foundation Ice Stream enters the RIS the maximum ice thickness exceeds 2000 m, but this value decreases rapidly to the north. In contrast, the adjacent Mollereisstrom (MES) shows ice thicknesses of only 1100-1200 m in the transition zone, whereas further west, on Institute Ice Stream, ice thicknesses of 1400-1500 m are found in the transition zone. In most parts of the southeastern RIS, the ice thicknesses still exceed 1000 m. A strong decrease in the meteoric ice thickness occurs in the central part of the eastern RIS, notably between Henry Ice Rise and Berkner Island and further north. There, a >350m thick marine ice layer underlies the meteoric ice (Reference ThyssenThyssen, 1988; Reference OerterOerter and others, 1992).

Analysis of the seismic data resulted in information on the ice thickness, the water-column thickness and the structure of the sea floor (Reference Lambrecht, Mayer, Hempel, Nixdorf and OerterLambrecht and others, 1997). The resulting ice-thickness values correspond well with the values determined from the RES measurements.

The seismic data along the entire profile indicate floating ice. Awater-column thickness of 500 m was calculated at about 83.12° S, the position previously supposed to be the grounding line, as derived from satellite data (IfAG, 1993).

Due to this contradiction, the position of the grounding line remains unclear, although the RES data contain further information. The difference between surface elevations calculated from ice thicknesses, using the flotation criterion, and elevations measured by aircraft laser altimetry indicates that the grounding line is about 40 km further south than previously assumed.

Accumulation Rates, Flow Velocities and Ice Flux

The accumulation-rate distribution, determined by using tritium concentrations, δ ¹⁸0 ratios and electrical conductivity measurements to date the ice cores (Reference Graf, Oerter, Mayer and LambrechtGraf and others, 1999), decreases from 18 cm w.e. a⁻¹ at the ice front to minimum values of 9 cm a⁻¹ around position 800 (Fig. 3). Further south, close to the Foundation Ice Stream grounding line and ascending to the inland ice, the accumulation rate increases again, reaching 17 cma⁻¹ at the southernmost location (position 1100).

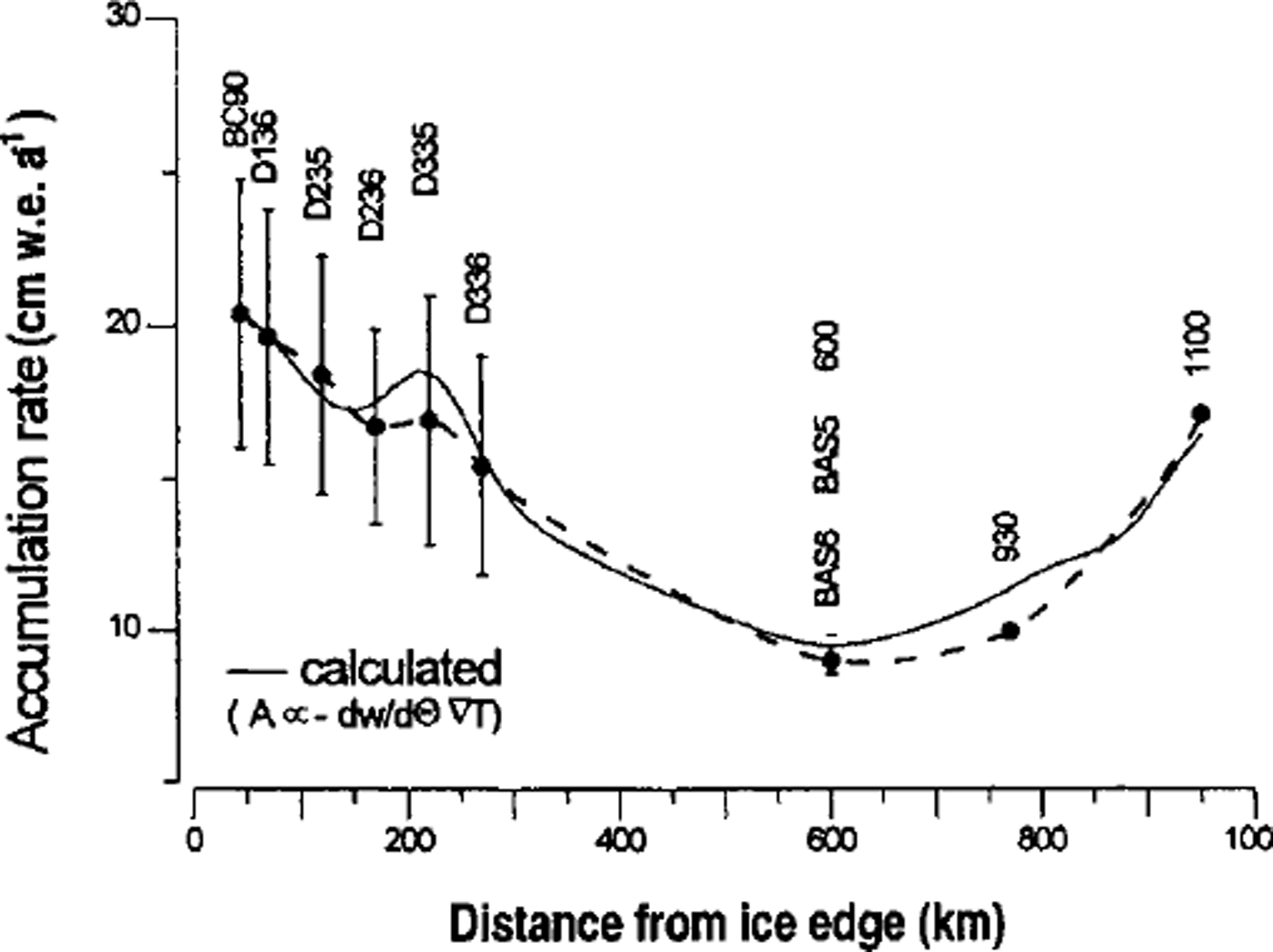
Fig. 3. Accumulation rates derived from stable-isotope ratios (dots) and a Rayleigh model of 10 m firn temperatures (solid line) ( Reference Graf, Oerter, Mayer and LambrechtGraf and others, 1999). The bars at the six positions denote the seasonal variability.

The observed flow velocity of Foundation Ice Stream just north of its grounding line is 586.5 m a⁻¹ (position 950). In flow direction, the velocity decreases to 208 m a⁻¹ south of Berkner Island (position 500). From there, spreading of the ice shelf results in increasing velocity towards the coast (Reference Riedel, Karsten, Ritter, Niemeier and OerterRiedel and others, 1995).

The calculated accumulation rates were converted into ice equivalent to match the derived ice fluxes. By combining the converted accumulation rates and the observed ice-flow data with ice-thickness information, we calculated a mass flux of 51 ± 5 km³ a⁻¹ for Foundation Ice Stream at its grounding line. For these calculations it was necessary to extrapolate the velocity from the southernmost measured position (950) to the actual position of the grounding line, 15 km to the south. The ice thickness in this area was obtained from RES profiles. Reference Mclntyre and KohnenMclntyre (1986) found a somewhat higher value of 59.4 km³ a⁻¹, assuming equilibrium conditions between the grounding-line flux and the accumulation in the drainage area. Extrapolation of the known velocities on the MES flowline resulted in a mass flux of 23 ± 5 km³ a⁻¹ for this ice stream.

Basal Melt Rates

Pressure dependence of the sea-water freezing point enables thermohaline convection underneath ice shelves (Reference RobinRobin, 1979), which initiates melting at the grounding line and freezing in the central part of the FRIS. This redistribution of ice and the induced latent-heat flux creates a thermodynamic equilibrium between the ice shelf and the adjacent sea water (Reference Lewis and PerkinLewis and Perkin, 1986; Reference JenkinsJenkins, 1991). Even with this effect of redistribution, the net melting of ice can account for a substantial part of the ice discharge from the grounded ice sheet.

Melt rates derived from thermohaline circulation modelling

One way of calculating basal melt rates is to apply a numerical model which describes the phase changes between ice and water depending on pressure, temperature, salinity and convection.

Along two RES profiles, following flowlines of Foundation Ice Stream and MES, respectively, the melt rates were calculated according to the numerical model of Reference Jenkins and BomboschJenkins and Bombosch (1995). A linear decrease in water temperature from −1.9°C at the sea surface to −2.3°C at 2200 m depth was assumed at the ice/water interface, according to model results of Reference Hellmer and JacobsHellmer and Jacobs (1992) and Reference Nicholls and JenkinsNicholls and Jenkins (1993). The results of our calculations are displayed in Figure 4. Close to the Foundation Ice Stream grounding line, the melt rates exceed 20 m a⁻¹, because of the high ice-thickness gradient in this area. Close to the grounding line, however, the model tends to produce exaggerated values (personal communication from A. Jenkins, 1996). Towards the sea, the melt rates decrease rapidly to almost zero, about 300 km from the grounding line. There, close to the southern tip of Berkner Island, suitable conditions for refreezing are predicted.

Fig. 4. Comparison of the melt rates from the thermohaline circulation model and from the continuity equation along the Foundation Ice Stream flowline, applied to geometry and strain rates at the different positions.

The melt rates beneath MES are much lower, showing a maximum of only 1.4 m a⁻¹. Along this flowline, the refreezing starts in the area west of southern Berkner Island. There, the refreezing rates reach values up to 2.2 ma⁻¹, due to the creation of frazil ice in the water column.

Melt rates derived from continuity and mass flux

The continuity equation for mass conservation can be written in terms of the basal melt rate:

(1)

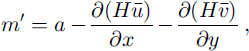
where m’ is basal melt rate, a is surface accumulation, H is ice thickness and ū, v are velocities.

For known accumulation, ice thickness and strain rates, it is possible to calculate the basal melt rate.

At locations where strain rates were measured, the basal melt rates vary from 8.8 ma⁻¹ in the south to 4.1 ma⁻¹ at the northernmost location. The melt rates calculated at these locations are displayed as columns in Figure 4. The width of the columns is proportional to the distance between the points used for the flux-divergence calculations. These results correspond well with the melt rates from the thermohaline modelling results, except at point 930 where the model predicts a somewhat higher value.

Melt rates derived from mass flux within flow bands are also in good agreement with the results of the model. The basal melt rate between two cross-profiles and two identified flowlines can be calculated if the ice thickness and velocity distribution on the two profiles and the surface accumulation rate are known. For this calculation close to the Foundation Ice Stream grounding line, several RES cross-profiles have been used. Characteristic channel-like features of the ice subsurface, which could be identified on every RES profile, allowed us to define several flowlines. The resulting subglacial melt rates range from 9.4 ± 0.8 ma⁻¹ in the south to 3.4 ± 1.0 m a⁻¹ further north (Fig. 5).

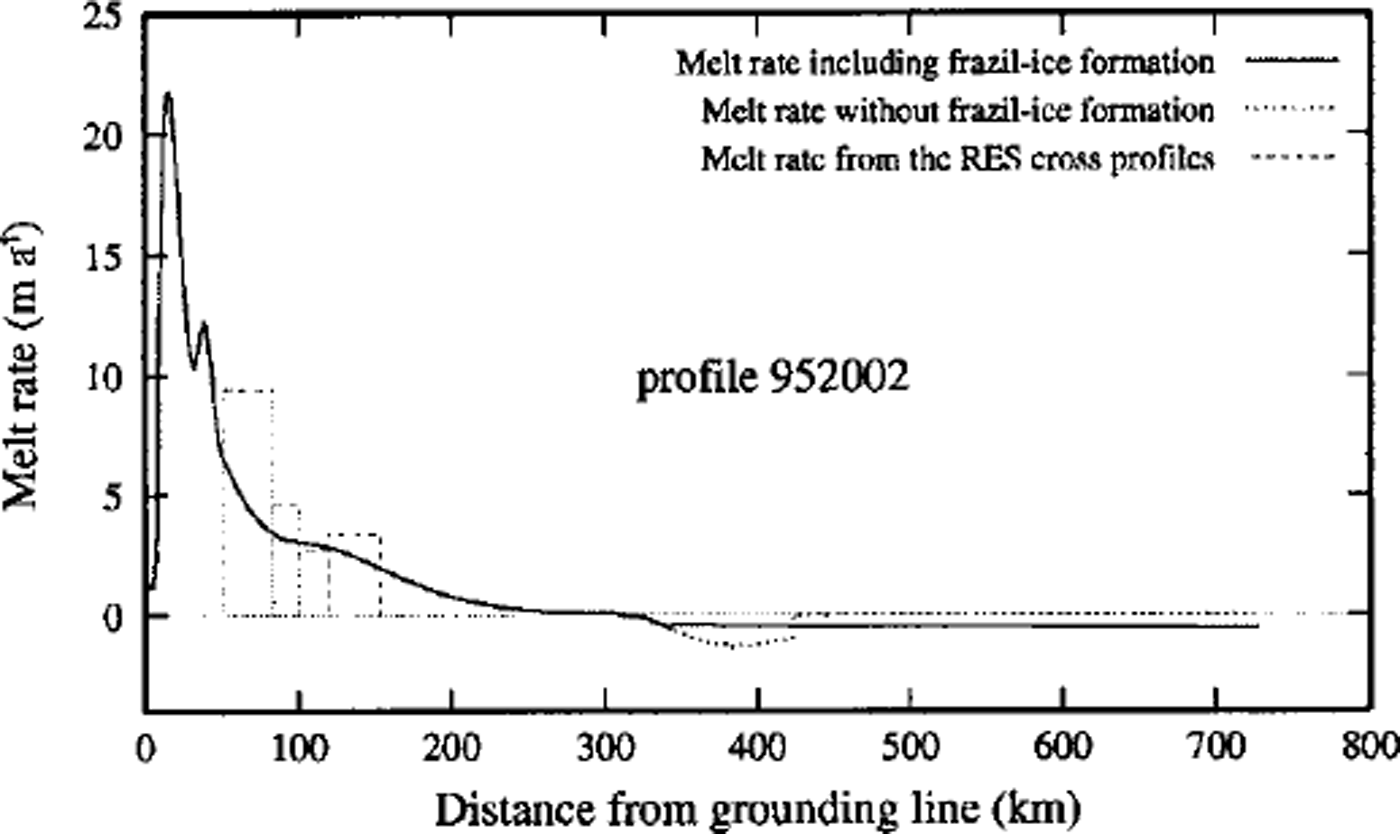
Fig. 5. Comparison of the melt rates from the thermohaline circulation model and from the different cross-profiles within a defined flow band along the Foundation Ice Stream flow line.

The melt rates calculated between the northern cross-profiles correspond well with the results of the thermohaline model. The increase in melt rates towards the grounding line starts earlier than predicted by the numerical model, possibly because of difficulties in accurately determining the flowlines. Due to the lack of field data, it is not possible to verify the very high melt rates calculated by the numerical model at the grounding line by other methods.

Mass Balance of the Southeastern Ris

As shown in Figure 6, the total mass input from Foundation Ice Stream and MES into the eastern RIS is 74 ± 10 km³ a⁻¹. Flow features on satellite images show that part of the ice volume transported by Foundation Ice Stream flows through the trough between Berkner Island and Dufek Massif into the Filchner Ice Shelf. Up to now, no flow velocities are available for this area south of Berkner Island. To calculate the mass balance, we therefore used results of a coupled ice-shelf-ocean model (Reference Grosfeld, Hellmer, Jonas, Sandhager, Schulte, Vaughan, Jacobs and WeissGrosfeld and others, 1998) which shows velocities of 80 ± 20 m a⁻¹ in this area (personal communication from H. Sandhager, 1997). Thus, the mass flux between 80.5033° S, 45.3247° W and 80.8394° S, 43.2432°W is 4 ± 2.5 km³ a⁻¹, using a flow-band width of 53 ± 2 km, determined from high-resolution satellite images, and a mean ice thickness of 900 ± 30 m across this flow band, derived from RES data. Measured ice velocities (Reference Riedel, Karsten, Ritter, Niemeier and OerterRiedel and others, 1995) and ice-thickness information from RES profiles result in a mass flux of 23 ± 2.2 km³ a⁻¹ between Henry Ice Rise and Berkner Island to the north. Balancing the mass flux of the contributing ice streams and the surface accumulation in the southeastern RIS with the outflow results in a residue of 53 ± 15.3 km³ a⁻¹, which must be melted from the underside of the ice shelf to satisfy mass conservation.

Fig. 6. Results for the mass-balance investigations of the southeastern RIS. The total mass flux into this ice-shelf area of 80 km³ a’¹ (from MES, Foundation Ice Stream and surface accumulation) is compensated by the discharge into the northern RIS (23 km³ a’), into the Filchner Ice Shelf (4 km³ a’¹) and basal melting of 53 km³ a’¹, which is even more than the total mass transported by Foundation Ice Stream (source for underlying maP: If AG (1993)). The black line southeast of Berkner Island represents the profile for the flux calculation into the Filchner Ice Shelf

Conclusions

The data collected during the Filchner Vexpedition form the basis for mass-balance calculations in the southeastern RIS. The derived mass flux for Foundation Ice Stream is almost double the flux for MES. The seismic measurements show that the grounding line is further south than previously assumed, and by using RES data a grounding-line position some 40 km further south was calculated. This result increases the area of the southeastern RIS by about 2000 km² The very thick ice found close to the new grounding-line position induces very high subglacial melt rates underneath Foundation Ice Stream, with values up to 9.4 ± 0.8 m a⁻¹. These are much higher melt rates than those underneath MES, as well as underneath the other ice streams around the FRIS, where maximum melt rates are in the order of 6 ma⁻¹ (Reference Bombosch and JenkinsBombosch and Jenkins, 1995). Averaged over the entire southeastern RIS, the mean subglacial melt rate is 0.9 ± 0.2 m a⁻¹, which is in good agreement with melt rates calculated from steady-state ice-shelf profiles (Reference Oerlemans and van der VeenOerlemans and Van der Veen, 1984; Reference LambrechtLambrecht, 1998). Comparison of the ice-stream flux with the melted volume reveals that >70% of the ice volume from the ice sheet does not reach the ice front as meteoric ice. This is confirmed by Reference Graf, Oerter, Mayer and LambrechtGraf and others (1999), who concluded from firn-core isotope data that all ice deposited south of position 1100 will be melted at the underside of the ice shelf before refreezing starts.