1. Introduction
Since the seminal propositions of the evolutionary search methods in 60’s and 70’s years, one of the main applications of these algorithms lies in optimization problems. Aiming to get these applications closer to solve relevant real-world tasks, optimization problems with multiple objectives turned out a hot topic in evolutionary optimization research in the last decades (Aghdasi et al., Reference Aghdasi, Saeedvand and Baltes2019; Coello, Reference Coello1999; Guliashki et al., Reference Guliashki, Toshev and Korsemov2009; Kakde, Reference Kakde2004). They are called multiobjective optimization problems (MOPs). On the other hand, dynamic optimization problems have also been broader investigated in the context of evolutionary computation field. However, the vast majority of these works were focused on mono-objective formulations, so they can be called as Dynamic Single-objective Optimization Problems (DSOPs) (Jin and Branke, Reference Jin and Branke2005). Recently, the dynamic nature of MOPs has been further investigated (Azzouz et al., Reference Azzouz, Bechikh and Said2017), enabling the cross-fertilization of the ideas employed in both multiobjective and dynamic optimization evolutionary strategies. Therefore, when an MOP has also a dynamic facet it is called a Dynamic Multiobjective Optimization Problem (DMOP). Taking DMOPs into account, the set of objectives or constraints changes over time. This characteristic makes DMOPs more challenging than MOPs and DSOPs, since the objective space modifies along the evolutionary search (Deb and Karthik, Reference Deb and Karthik2007) and involves multiple objectives at the same time.
Evolutionary algorithms (EAs) are especially suited for multiobjective optimization problem as they deal with a population of points in the search space rather than a single problem solution. The EA framework is characterized by a population of candidates for solutions and the reproduction process allows the combination of existing candidates to generate new ones. This allows the evolutionary search to find several members of the Pareto Optimal in a single run, instead of performing a series of separate runs, which is the case with some of the conventional stochastic processes (Horn et al., Reference Horn, Nafpliotis and Goldberg1993). Moreover, EAs can be adapted easily to different problems, regardless of how their objectives and constraints are represented. This flexibility is even more important when dealing with dynamic problems, as these characteristics—objectives and constraints—may change over time. The strategies for building a new population at each environment change in a DMOP are based on two principles (Hatzakis and Wallace, Reference Hatzakis and Wallace2006): (i) inserting diversity to explore unreachable regions in the new environment; (ii) use information from the previous environment to guide the search in the new environment. These two characteristics fit well with the genetic algorithm (AG), since it optimizes several solutions simultaneously, making it possible to reuse the information from an environment to another, while allowing for the maintenance of diversity from the introduction of unexplored points of the search space.
Although works investigating multiobjective evolutionary algorithms (MOEAs) applied to dynamic problems have gained a lot of strength in recent years (Azzouz et al., Reference Azzouz, Bechikh and Said2017), it is still common to find DMOPs that are limited to two or three objectives in the literature. The greater the number of objectives involved in an MOP, the greater the challenge for the EAs. The main reason to this is because the increment in the number of objectives causes a significant increase in the number of nondominated solutions, decreasing the selective pressure of the search (Ishibuchi et al., Reference Ishibuchi, Tsukamoto and Nojima2008). Formulations using four or more objectives characterizes the many-objective optimization problems (MaOPs). In two recent papers (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b), the authors worked with the Dynamic Multiobjective Knapsack Problem (DMKP) (Farina et al., Reference Farina, Deb and Amato2004) using formulations with more than three objectives.
Some EAs found in the literature and proposed for dynamic MOPs were evaluated in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), for DMKP instances with 4, 6, and 8 objectives. The EAs investigated were: Dynamic Nondominated Sorting Genetic Algorithm II (DNSGA-II) (Deb and Karthik, Reference Deb and Karthik2007), Multi-strategy Ensemble MOEA (MS-MOEA) (Wang and Li, Reference Wang and Li2010), and Multiobjective Evolutionary Algorithm with Decomposition with Kalman Filter (MOEA/D-KF) (Muruganantham et al., Reference Muruganantham, Tan and Vadakkepat2016). The Nondominated Sorting Genetic Algorithm III (NSGA-III) (Deb and Jain, Reference Deb and Jain2014) was proposed to deal with static many-objective problems. Therefore, a variation of the NSGA-III was also proposed in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a) adapting it to DMOPs called DNSGA-III. The multiobjective metrics employed were hypervolume-ratio (Zitzler and Thiele, Reference Zitzler and Thiele1999) and IGD* (Wang and Li, Reference Wang and Li2009). Experimental results have shown that the MS-MOEA algorithm, which uses an evolutionary strategy based on memory, obtained the best multiobjective solutions in the adopted metrics and overcame the other MOEAs both in convergence and in diversity. However, it demands a much longer execution time than the other investigated algorithms. DNSGA-II was in second place, even surpassing DNSGA-III and MOEA/D-KF, but with a much shorter execution time than MS-MOEA. An additional evaluation was introduced in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), comparing MS-MOEA with a proposed variation of DNSGA-II, in which an external file was incorporated to the framework, similar to the strategy used by MS-MOEA. This proposal was called DNSGA-II*, which showed a better performance when compared with DNSGA-II. However, even with this refinement, it did not achieve the convergence results of MS-MOEA. Few environment changes were applied during the evolutionary experiments in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), limiting them to one or two modifications in one of the objectives. Besides the DMKP instances involves a set of 30 or 50 items to be packaged in the knapsack.
MOEAs were also applied to the DMKP in a subsequent work (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b). The investigated DMKP instances involve sets of 30 or 50 items and the number of environment changes was increased to 5 and 10 modifications, turning it possible to investigate MOEAs behavior in more dynamic scenarios. However, due the intrinsic increment in the complexity of these new scenarios, just formulations using four and six objectives were analyzed, being that ten environment changes was possible to analyze just using 4 objectives. Moreover, the authors also presented a new version of the Many-objective Evolutionary Algorithm Based on Nondominated Decomposed Sets (MEANDS) (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016), that was originally proposed for static MaOPs, in which an evolutionary strategy based on memory was incorporated to the basic MEANDS framework to solve DMOPs. This proposition was called Dynamic Many-objective Evolutionary Algorithm Based on Nondominated Decomposed Sets (D-MEANDS) and it was proposed to solve DMaOPs. A performance analysis compared its results with the two most promising algorithms in the earlier work: MS-MOEA and DNSGA-II*. In general, D-MEANDS outperformed the other two MOEAs in all the multiobjective metrics used. However, it was observed that as the instances of the problem become more complex, the execution time increases significantly compared with other algorithms, mainly when 6 objectives are used in the formulation.
In the present work, we promote a deeper investigation of the adaptation of the MOEAs to dynamic optimization environments. The problem at hand is also the DMKP (Farina et al., Reference Farina, Deb and Amato2004). However, more complex DMKP instances are employed here: sets of 30, 50 and 100 items subject to formulation using 4, 6, and 8 objectives. Moreover, the environment are subject to more modifications, from 10 to 20 changes, enabling us to investigate more dynamic scenarios. One of the main limitations in the previous works (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) to investigate more complex and dynamic instances of DMKP was due to the employment of parametric metrics, which depend on the computation of Pareto approximations, as they demand a high computational cost. On the other hand, non-parametric metrics are employed here: density and hypervolume. It enabled us to use more challenging instances and to increase the number of generations compared with the previous works.
We started our analysis using the same algorithms investigated in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b): DNSGA-II* (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), MS-MOEA (Wang and Li, Reference Wang and Li2010) and D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b). In addition, we propose an adaptation of D-MEANDS in which an additional diversity strategy is incorporated, impacting both on convergence and diversity. This new version is called Dynamic Many-objective Evolutionary Algorithm based on Nondominated Decomposed Sets with Memory and Diversity (D-MEANDS-MD). Moreover, we included a recent MOEA proposed for dynamic MOPs in our comparison: the DDIS-MOEA/D-DE (Liu et al., Reference Liu, Peng, Liu and Liu2020), which uses differential evolution as its underlying evolutionary search framework and a diversity introduction strategy to deal with dynamical MOPs. All algorithms investigated here use dynamic strategies based on diversity and memory. In previous work (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), a prediction-based algorithm was evaluated for solve DMKP and presented a significant lower performance than the other MOEAs based on diversity and memory. For this reason, we will address in this work only these two strategies (diversity and memory).
According to the authors in (Helbig et al., Reference Helbig, Deb and Engelbrecht2016), one of the key challenges for solving DMOPs would be the adaptation of many-objective optimization algorithms to dynamic problems. They also postulated that “no work on dynamic many-objective optimization has been published” until that time. We also performed a carefully research on the literature seeking for papers investigating dynamic optimization from a many-objective perspective and to the best of our knowledge the first published works on this thematic are (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b), which are the basis from where we start this investigation. The present work is the first that deepened in this question involving scenarios with several objectives (up to 8) and a considerable number of environment changes (up to 20). Furthermore, we present a new proposal of MOEA which achieved the best hypervolume and diversity on the instances of a discrete DMOP.
The rest of this paper is organized as follows. Section 4 The MOEAs used in this work, including the novel algorithm D-MEANDS-MD. Section 2 introduces the concept of dynamic multiobjective optimization problems (DMOPs) and presents our formulation to a dynamic version of the Multiobjective Knapsack Problem (DMKP). Section 3 reviews related work on the MOEAs applied to DMOPs. Section 5 depicts the experiments performed to evaluate the dynamic MOEAs and the results achieved. Finally, Section 6 presents some conclusions and briefly describes ongoing and future work.
2. Problem formulation
MOPs are characterized by having more than one objective to be optimized. Unlike mono-objective optimization, MOPs usually have more than one optimal solution to be found, since their objectives may be in conflict (Radulescu et al., Reference Radulescu, Mannion, Zhang, Roijers and Nowé2020), that is, to improve one objective the search depreciates another one. However, it is still possible to define whether one solution is better than another in the search space for an MOP considering the concept of dominance proposed by Pareto (Mannion et al., Reference Mannion, Devlin, Duggan and Howley2018). We can determine that a solution x dominates another solution y (
![]() $x \prec y$
in a minimization problem) if x is better than y in at least one objective and is not surpassed in the others. When one solution is not dominated by any other in the entire search space, it belongs to the set of the best solutions of the MOP, which is called Pareto Optimal (
$x \prec y$
in a minimization problem) if x is better than y in at least one objective and is not surpassed in the others. When one solution is not dominated by any other in the entire search space, it belongs to the set of the best solutions of the MOP, which is called Pareto Optimal (
![]() $P^*$
). Therefore, the purpose of a multiobjective evolutionary algorithm is to find
$P^*$
). Therefore, the purpose of a multiobjective evolutionary algorithm is to find
![]() $P^*$
or at least a set of solutions close to it (Pareto approximation).
$P^*$
or at least a set of solutions close to it (Pareto approximation).
Consider a problem P with m objectives and
![]() $\Omega$
the set of all possible solutions of P (search space). An MOP to minimize the objectives of P is mathematically formulated as:
$\Omega$
the set of all possible solutions of P (search space). An MOP to minimize the objectives of P is mathematically formulated as:
where x is a solution of the search space (
![]() $x \; \epsilon \; \Omega$
);
$x \; \epsilon \; \Omega$
);
![]() $f_i(x)$
refers to the value of the i-th objective for x (
$f_i(x)$
refers to the value of the i-th objective for x (
![]() $i = 1, ..., m$
); and functions g(x) and h(x) represent respectively the set of constraints of inequality and equality of the problem. In this context, we can say that x dominates y (
$i = 1, ..., m$
); and functions g(x) and h(x) represent respectively the set of constraints of inequality and equality of the problem. In this context, we can say that x dominates y (
![]() $x \prec y$
) if and only if:
$x \prec y$
) if and only if:
Although the DMOPs maintain the same concept of dominance used in its static version, they are characterized by dealing with changes in the environment (objectives and constraints of the problem) over time. These changes impact in the objective space, modifying the Pareto Front. Therefore, MOEAs used in dynamic optimization must have a fast convergence to a good approximation of the Pareto Optimal whenever the environment changes. A DMOP can be formally defined as:
where, t represents the time or dynamic nature of the problem. That is, the mathematical formulation in Equation (1) is adapted so that its functions consider changes in the environment at time t.
Two other concepts related to dynamic problems are severity and frequency of the change (Richter, Reference Richter2013). The severity of the change means how strong it is in terms of magnitude, that is, as greater is the change as greater is its impact on the space of objectives. The frequency of change determines how often the environment changes. When changes occur very quickly, the evolutionary algorithm may not have enough generations to converge on a reasonable Pareto approximation.
Given a knapsack that supports a certain weight limit Q and a set of all available items I, each one with its respective weight
![]() $w_i$
and value
$w_i$
and value
![]() $v_i$
(
$v_i$
(
![]() $i \; \epsilon \; I$
), the Knapsack Problem (KP) (Kellerer et al., Reference Kellerer, Pferschy and Pisinger2004) consists of choosing a subset
$i \; \epsilon \; I$
), the Knapsack Problem (KP) (Kellerer et al., Reference Kellerer, Pferschy and Pisinger2004) consists of choosing a subset
![]() $I^*$
of items I in order to maximize the total value of the collected items. However, the sum of the weights of these items cannot exceed the weight limit of the knapsack (Q). In the multiobjective version of Knapsack Problem (MKP) (Ishibuchi et al., Reference Ishibuchi, Akedo and Nojima2013), each item
$I^*$
of items I in order to maximize the total value of the collected items. However, the sum of the weights of these items cannot exceed the weight limit of the knapsack (Q). In the multiobjective version of Knapsack Problem (MKP) (Ishibuchi et al., Reference Ishibuchi, Akedo and Nojima2013), each item
![]() $i \; \epsilon \; I$
has a value of
$i \; \epsilon \; I$
has a value of
![]() $v_i,_j$
and a weight of
$v_i,_j$
and a weight of
![]() $w_i,_j$
for an objective j. The purpose of the algorithm is to find a subset of items
$w_i,_j$
for an objective j. The purpose of the algorithm is to find a subset of items
![]() $I^*$
(
$I^*$
(
![]() $I^* \; \subseteq \; I$
), respecting the weight constraint of each objective (
$I^* \; \subseteq \; I$
), respecting the weight constraint of each objective (
![]() $Q_j$
), while maximizing their respective values. This multiobjective problem is formulated as:
$Q_j$
), while maximizing their respective values. This multiobjective problem is formulated as:
 \begin{gather}\sum_{j=1}^{m} \left[\left(\max \sum_{i=0}^{n} v_{i,j}*x_i\right);\left(\sum_{i=0}^{n} w_{i,j}*x_i \leq Q_j\right)\right]\end{gather}
\begin{gather}\sum_{j=1}^{m} \left[\left(\max \sum_{i=0}^{n} v_{i,j}*x_i\right);\left(\sum_{i=0}^{n} w_{i,j}*x_i \leq Q_j\right)\right]\end{gather}
Consider a set of items I, where
![]() $i = 0, ..., n$
and a set of objectives J, where
$i = 0, ..., n$
and a set of objectives J, where
![]() $j = 1, ..., m$
;
$j = 1, ..., m$
;
![]() $x_i$
is a binary value that receives 1 when item i is in the knapsack and 0 otherwise;
$x_i$
is a binary value that receives 1 when item i is in the knapsack and 0 otherwise;
![]() $Q_j$
is the maximum weight for an objective j.
$Q_j$
is the maximum weight for an objective j.
The DMKP is an extension of the MKP, where the objectives and/or constraints are modified in each environment change (Branke, Reference Branke2001). Different instances were generated for the DMKP, varying the number of environmental changes (10, 15, and 20 changes), items (30, 50 and 100 items) and objectives (4, 6, and 8 objectives). Therefore, the experiments were performed using 27 instances of the problem. For each instance, we first built a static MKP configuration to represent the initial environment, which is modified progressively after the changes emerge. The initial environment is built based on the procedure described in (Martello and Toth, Reference Martello and Toth1990) and refined in (Franca et al., Reference Franca, Martins and Oliveira2018): a set of objective functions was generated containing the value and weight of each item and the maximum weight that the knapsack can support for that objective. In (Martello and Toth, Reference Martello and Toth1990) random instances were generated using the interval of [0, 100] for the value and weight of each item. Following the same idea, we generate our instances using the interval [0, 1000]. We believe that the interval [0, 100] is small considering the number of items we use in each instance (instances with up to 100 items were generated), as it could generate repeated values between items frequently as the values are integers. Besides, Martello suggested calculating the knapsack capacity constraint by summing the weights of all the items and multiplying it by 0.5 (Martello and Toth, Reference Martello and Toth1990); according to him, this guarantees that half of the items would be in the knapsack of the best solution. In our experiments, we multiply the weights sum by 0.6 to have more items in the non-dominated solutions, that is, in general 60% of the possible items are allocated in the knapsack regarding the non-dominated solutions. We believe that using more diversity related to the best solutions, we could generate problems where the Pareto Optimal has more non-dominated solutions. This makes the comparison of algorithms more effective since we deal with more complex instances. The same procedure was applied to (Franca et al., Reference Franca, Martins and Oliveira2018).
In our formulation of the DMKP, we adopted a low severity of change, in which only one objective is modified per environmental change (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b). At each change of environment (CE), one of the set of items is changed, altering the search space and the related Pareto Optimum. Starting from the initial environment the changes will be applied after a fixed interval of generations. Changing an objective means modifying the values and weights of the set of items associated with that objective. Changes in constraint consist of using knapsacks with different capacities (weight limit associated to each objective) Although changes are made directly to the set of items for the objective chosen to be modified (Farina et al., Reference Farina, Deb and Amato2004), a change of the value of the Qj capacity constraint (maximum weight) associated to same objective is also promoted. The weights are modified when new items are generated in the interval [0, 1000] and the value of Qj is recalculated multiplying the sum of the weights of all items by 0.6. In that way, although the absolute value of the constraint is modified for one objective, this change keeps the proportion of items around 60% of the total set. In that way, we are able to modify the Qj value without promoting a big impact on the selective pressure of the search space. By modifying in each environmental change just one set of n items associated to one of the m objectives we are able to perform a more controlled experiment, in which the severity of change is not high and we could choose the number of objectives to be modified (one in each time) in a complete execution. On the contrary, the adoption of a high severity of change could considerably modify the Pareto set in a such way that would be better to start the search again from scratch (Branke, Reference Branke2001).
The knapsack problem (KP) is one of the most studied combinatorial problems in the literature (Farina et al., Reference Farina, Deb and Amato2004; Ishibuchi et al., Reference Ishibuchi, Akedo and Nojima2013; Kellerer et al., Reference Kellerer, Pferschy and Pisinger2004; Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Mannion et al., Reference Mannion, Devlin, Duggan and Howley2018). Instances of this problem—including KP, MKP, and DMKP variations- appear in real-world decision-making processes related to different areas. For example, in the financial field, selecting assets to build portfolios can be considered as a KP instance. In this case, the financial advisor must select which investments and holdings current available in the market—such as stocks, bonds, mutual funds, commodities, cryptocurrencies, and cash—should be allocated in a personal portfolio to maximize the return. Besides, this selection is subject to some constraints including the total amount of money to invest and liquidity needs. One may model this optimization problem as the simplest version of KP, considering a static market and a single objective function to evaluate the portfolio under construction. This scalar assessment is often performed using a weighted sum of relevant factors to be considered, such as risk, return objectives, and time horizon. However, in the real-world application, the best setting of these factor weights is difficult to determine. Therefore, modeling this application by a multiobjective approach could be better since the objectives are individually manipulated and the investor could choose the best portfolio from a set of possibilities generated by a multiobjective optimizing tool. Additionally, the financial market is a dynamic environment where the indices related to each asset fluctuate frequently throughout the day. Therefore, this decision-making process is best modelled as a DMKP instance.
In fact, several real-world decision-making processes are best modelled as instances of dynamic, many-objective optimization problems. However, they are more difficult to handle by optimization methods in general. Multiobjective evolutionary approaches are also challenged by this class of problems since the employment of many objectives imposes a very high selection pressure and the intrinsic dynamism imposes the need to update the set of approximate Pareto solutions as new changes emerge. This work intends to advance in the optimization of dynamic and many-objective problems through the development of new EAs.
3. Related work
This work focus on the application of EAs to solve DMOPs. In this section, we review some of the major studies from the literature that proposed evolutionary approaches to solve multiobjective problems in general. We organized this session into two subsections. Subsection 3.1 presents works dedicated to the investigation of MOEAs to handle static MOPs, which are more common on the specialized literature. Subsection 3.2 discusses studies that proposed MOEAs for dynamic MOPs.
3.1. MOEAs proposed for Multiobjective Optimization Problems (MOPs)
In the early 1960s, Rosenberg proposed an evolutionary algorithm (EA) to solve MOPs. However, just from 1980s that evolutionary multiobjective optimization (EMO) and MOEAs have become a hot topic in the evolutionary computing research. (Mao-Guo et al., Reference Mao-Guo, Li-Cheng, Dong-Dong and Wen-Ping2009).
Multiobjective optimization methods based on EAs can be grouped into three research stages. In the first MOEAs (1993-1998), such as MOGA (Fonseca and Fleming, Reference Fonseca and Fleming1993), NPGA (Horn et al., Reference Horn, Nafpliotis and Goldberg1994), and NSGA (Srinivas and Deb, Reference Srinivas and Deb1994), the selection method was formally based on non-dominance classification and the population diversity strategies adopted a fitness sharing mechanism. Works developed around 1995–2002 focused in the refinament of the MOEAs, proposing selection methods based on external archiving strategies and different approaches for the individuals ranking of the population in a non-dominant environment. NSGA-II (Deb et al., Reference Deb, Pratap, Agarwal and Meyarivan2002), SPEA (Zitzler and Thiele, Reference Zitzler and Thiele1999), SPEA-II (Zitzler et al., Reference Zitzler, Laumanns and Thiele2001), and PAES (Knowles and Corne, Reference Knowles and Corne1999) are some examples of this category of algorithms.
Since then, several multiobjective algorithms have emerged, most investigating problems with 2–3 objectives. Among them, we can mention ParEGO, one of the first and simplest extensions of the EGO algorithm for MOPs (Knowles, Reference Knowles2006). ParEGO sequentially scales the multiobjective problem with weights that are iteratively updated to explore the Pareto front. In 2007, Zhang and Li (Reference Zhang and Li2007) proposed a Decomposition-based MOEA (MOEA/D) combining traditional mathematical programming methods with EAs. Ho and Tay (Reference Ho and Tay2007) presented an efficient approach to solve the flexible multiobjective job-shop combining evolutionary algorithm and guided local search. In 2010, an improved GA based on the principle of immunity and entropy is used to solve the multiobjective flexible job-shop scheduling problem proposed by (Wang et al., Reference Wang, Gao, Zhang and Shao2010). Pizzuti proposed in 2011 the Multiobjective Genetic Algorithms for Networks (MOGA-Net) to discover communities in networks using genetic algorithms (Pizzuti, Reference Pizzuti2011). The method optimizes two objective functions introduced in 2009 for Lancichinetti et al. (Reference Lancichinetti, Fortunato and Kertész2009), that proved to be effective in detecting modules in complex networks. The first objective function employs the concept of community scoring to measure the quality of a network’s community division. The second function defines the concept of capability of nodes belonging to a module and iteratively locates the modules with the highest sum of capability of the node, hereinafter referred to as community capability. In 2012, a method that creates projections of current solutions and propagates equidistant interpolations in a non-dominant environment was presented by (Gu et al., Reference Gu, Liu and Tan2012) and demonstrated to obtain uniformly distributed optimal Pareto solutions. A new opposition self-adaptive hybridized differential evolution algorithm was proposed by Chong and Qiu (2016) (Chong and Qiu, Reference Chong and Qiu2016) to deal with continuous MOPs. Bradford et al. (2018) (Bradford et al., Reference Bradford, Schweidtmann and Lapkin2018) proposed an algorithm to approximate Pareto sets in a small number of function evaluations. The algorithm extends the well-known Thompson sampling (TS) method from the multi-armed bandit community (Thompson, Reference Thompson1933) to continuous multiobjective optimization. The algorithm was named ‘Thompson Sampling Efficient multiobjective Optimization’ (TSEMO).
The increase in the number of objectives brought an additional challenge, since the Pareto Fronts also increased in size. Therefore, it was common for EAs to find clusters of solutions in the search space that belonged to the same Front. Thus, problems with 4 or more objectives started to be classified as many-objective problems. Algorithms such as NSGA-II and SPEA2 presented difficulties in finding the best solutions for this type of problem and several algorithms and approaches have been proposed to solve many-objective problems. One of the most successfully used indicator-based MOEAs is the S-Metric-Selection EMOA (SMS-EMOA) (Emmerich et al., Reference Emmerich, Beume and Naujoks2005). SMS-EMOA invokes the non-dominated classification, which is used as a ranking criterion. Then it uses the hypervolume indicator as a selection mechanism to rule out the individual contributing the smallest hypervolume (the worst ranked). Deb and Saxena (2006) (Deb and Saxena, Reference Deb and Saxena2006) proposed the Principal Component Analysis-NSGA-II algorithm called PCA-NSGA-II. This algorithm combines a reduction technique with NSGA-II to deal with the redundance of objectives in MaOPs. In fact, many real-world problems have M objectives, while the true Pareto front is smaller than M-dimensions, that is, some of the objectives are redundant. herefore, the authors use the PCA method to determine the true Pareto optimal. In 2007, Sato et al. (Reference Sato, Aguirre and Tanaka2007) proposed a method to control the area of dominance of solutions in order to induce the proper classification of solutions for the problem in question, improving the selection and the performance of MOEAs in combinatorial optimization problems. The proposed method can control the degree of expansion or contraction of the dominance area of the solutions using a user-defined S parameter. In their experiments, the authors used the NSGA-II to solve MKP instances with five objectives. In order to solve large-scale problems, Garza-Fabre et al. proposed three different ways to rank solutions of the same Pareto front, which were called Global Detriment (GD), Profit (Pf) and Distance to the Best known solution (GB). Aiming to evaluate their proposal, the authors used a generic multiobjective GA (Garza-Fabre et al., Reference Garza-Fabre, Pulido and Coello2009). Said et al. (2010) (Said et al., Reference Said, Bechikh and Ghédira2010) proposed a new dominance relationship called r-dominance (dominance based on reference solution) that creates a strict partial order between equivalent Pareto solutions and is able to differentiate between partially non-dominated solutions based on a solution provided by user aspiration level vector. In ther experiments, the authors implemented r-dominance in the NSGA-II and evaluated it on problems from 2 to 10 objectives. Singh et al. (2011) (Singh et al., Reference Singh, Isaacs and Ray2011) presented the Pareto Evolutionary Singing Algorithm (PCSEA). The authors proposed a new approach that identifies a reduced set of objectives rather than dealing with the true dimensionality of true MaOP. Furthermore, the PCSEA does not approach the entire Pareto front, but seeks a specific set of non-dominated solutions. More specifically, the authors suggested using Pareto front limits called corner solutions to predict the dimensionality of the true Pareto front. Many-Objective Meta-heuristic Based on the R2 Indicator (MOMBI) (Gómez and Coello, Reference Gómez and Coello2013), is an algorithm proposed in 2013, that produces an non-dominated classification scheme based on utility functions. The main idea is to cluster solutions that optimize the set of utility functions and give them the first ranking. These solutions will then be removed and a second rank will be identified in the same way. The process will continue until all members of the population are classified. Asafuddoula et al. (2013) proposed the Decomposition Based Evolutionary Algorithm for Many-Objective Optimization with Systematic Sampling and Adaptive Epsilon Control (DBEA-Eps) (Asafuddoula et al., Reference Asafuddoula, Ray and Sarker2013). This algorithm is based on decomposition generating a structured set of reference points, which uses an adaptive epsilon comparison to managing the balance between convergence and diversity, and adopting an adaptive epsilon formulation to deal with constraints. Deb and Jain (2014) (Deb and Jain, Reference Deb and Jain2014) proposed a variation of the NSGA for many-objective optimization (NSGA-III), which was later extended to solve generic constrained many-objective optimization problems (Jain and Deb, Reference Jain and Deb2014). Elarbi et al. (2016) (Elarbi et al., Reference Elarbi, Bechikh, Said and Hung2016) proposed a new dominance relation called TSD-dominance to deal with many-objective problems and introduced it in NSGA-II. TSD-NSGA-II represents a new version of many-objective NSGA-II, where Pareto dominance is replaced by TSD dominance. It was considered highly competitive in the treatment of both restricted and unrestricted problems. In Cheng et al. (2016) (Cheng et al., Reference Cheng, Jin, Olhofer and Sendhoff2016) a reference vector-driven evolutionary algorithm for many-objective optimization was presented that balances convergence and diversity of solutions in a high-dimensional objective space. Lafetá et al. (2016) (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016) proposed MEANDS, an evolutionary algorithm for many-MOPs based on sub-populations, which represent sets of non-dominated solutions for different instances of subproblems, combining from two to all objectives. Lafetá and Oliveira (2019) (Lafeta and Oliveira, Reference Lafeta and Oliveira2019) present a new version of MEANDS, the MEANDS-II, which adapts to many-MOPs with a very large search space. In 2017, Elarbi et al. (Reference Elarbi, Bechikh, Gupta, Said and Ong2017) proposed the RPD-NSGA-II, an algorithm that integrates a new form of dominance, called RP-dominance, and NSGA-II. RP-dominance assigns penalties to some solutions, so it can classify solutions from the same front. Li et al. (2019) (Li et al., Reference Li, Wei, Song and Liu2019) proposed an efficient objective reduction method called ORSAP. The method is divided into two steps: initially, it uses a sampling algorithm to collect points that can represent objectives, calculating the improvements to the objectives. Then affinity propagation is adopted to cluster the objectives so that redundant ones can be grouped. Therefore, only the centroid objectives are kept in the non-redundant set. Li et al. (2020) (Li et al., Reference Li, He, Liang and Quan2020) proposed the Dividing-based Many-objective Evolutionary Algorithm for large-scale Feature Selection (DMEA-FS). The algorithm models the variables to adjust the solutions to a new search space that is more organized and easier to select the most promising solutions.
3.2. MOEAs proposed for Dynamic Multiobjective Optimization Problems (DMOPs)
Different strategies have been proposed to adapt traditional EAs to deal with DMOPs. Each strategy behaves differently when it comes to changing the environment (modifying the objectives and constraints of the problem). The most intuitive strategy would be to restart the population of MOEAs at each change of environment, but it proved to be a weak approach in (Branke, Reference Branke2001). The majority of the methods proposed for DMOPs in the literature use the knowledge of the population from the previous environment to streamline the search in the new environment (Jin and Branke, Reference Jin and Branke2005). The strategies employed during the change of environment usually concern with boosting convergence and diversity for the new environment. Three main types of strategies can be observed in the related work (Azzouz et al., Reference Azzouz, Bechikh and Said2017): (i) introduction of diversity (Deb and Karthik, Reference Deb and Karthik2007); (ii) forecast (Koo et al., Reference Koo, Goh and Tan2010); and (iii) memory (Cámara et al., Reference Cámara, Ortega and Toro2007). Some of the most relevant MOEAs proposed for DMOPs are presented following, where they are grouped for each kind of strategy.
(i) Introduction of diversity: Deb and Karthik (Reference Deb and Karthik2007) extended the well-known NSGA-II algorithm to deal with DMOPs, introducing diversity with each detection of change. This extension was named DNSGA-II and it is described in the next section since it is one of the MOEAs investigated in the experiments of Section 5. The DOMOEA algorithm (Orthogonal multiobjective EA for DMOP) was introduced in (Zeng et al., Reference Zeng, Chen, Zheng, Shi, de Garis, Ding and Kang2006), where two types of crossovers were used to improve diversity and intensify convergence: orthogonal crossover (Zeng et al., Reference Zeng, Chen, Zheng, Shi, de Garis, Ding and Kang2006) and linear crossover (Wright, Reference Wright1991). In 2007, Zheng et al. (Zheng, Reference Zheng2007) proposed a MOEA adapted for DMOPs called DMOEA. Basically, when a change of environment happens, DMOEA selects a set of the best individuals to mutate using hypermutation (Cobb, Reference Cobb1990) and the rest of the population is replaced by new individuals generated at random. In 2009, Chen et al. (Reference Chen, Li and Chen2009) proposed to explicitly maintain genetic diversity, considering it as an additional objective in the optimization process. They presented the Individual Diversity MultiObjective Optimization Evolutionary Algorithm (IDMOEA), which uses a new method for assessing the preservation of diversity, called Individual Diversity Evolutionary Method (IDEM). The purpose of IDEM is to add a useful selective pressure aimed at Pareto Front and to maintain diversity. An adaptation of the DNSGA-II was proposed by Azzouz et al. (Reference Azzouz, Bechikh and Ben Said2015) in 2015 to deal with dynamic constraints, replacing the constraint handling mechanism used with a more elaborate and self-adaptive penalty function. The resulting algorithm is called Dynamic Constrained NSGA-II (DC-NSGA-II). A new strategy for introducing diversity was proposed by Liu et al. (Reference Liu, Peng, Liu and Liu2020) in 2020, thus generating a MOEA called DDIS-MOEA/D-DE. In this proposal, the information generated during the evolution is recorded in preparation to assess the intensity of the change. Two strategies for introducing diversity are used to maintain the balance between convergence and diversity when an environmental change is detected. An improved inverse modeling is used for the drastic changes, while random initialization of partial solutions is used for the light changes. In 2020 Lafetá and Oliveira (Reference Lafetá and Oliveira2020a) proposed DNSGA-II*; another adaptation of DNSGA-II, where an external archive (Bosman and Thierens, Reference Bosman and Thierens2003) was introduced. A variation of the NSGA-III (Deb and Jain, Reference Deb and Jain2014) was also proposed in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a) adapting it to dynamic MOPs and it was called DNSGA-III.
(ii) Forecast: Hatzakis and Wallace (Reference Hatzakis and Wallace2006) presented in 2006 a forecasting technique called feed-forward prediction strategy in order to estimate the location of the Pareto Optimal. Then, an anticipated population (named forecast set) is used to accelerate the discovery of the next set of solutions. In 2007, Zhou et al. (Reference Zhou, Jin, Zhang, Sendhoff and Tsang2007) proposed the prediction of the new locations of various Pareto solutions in the decision space once a change is detected. Then, individuals in the reinitialized population are generated around these predicted points. The method called Dynamic Multiobjective Evolutionary Algorithm with Predicted Re-Initialization (DMEA/PRI) works with two strategies to reinitialize the population. The first strategy predicts the locations of new individuals, based on changes from previous points. The population is then partially or completely replaced by the new individuals generated based on this forecast. The second strategy includes a predicted Gaussian noise to the population, where the variation is estimated according to previous changes. In 2008, Roy and Mehnen (Reference Roy and Mehnen2008) proposed an adaptation of DNSGA-II (Deb and Karthik, Reference Deb and Karthik2007) that uses prediction and convenience functions. While in DNSGA-II, the diversity is introduced by adding random solutions, the parent population in this proposition is discarded and only the children are reevaluated before the algorithm is restarted. The objective functions are transformed using preference functions (Mehnen et al., Reference Mehnen, Trautmann and Tiwari2007) in order to guide the search toward the most interesting parts of the Pareto Front, according to the preferences of an expert or decision maker. In 2010, Koo et al. (Reference Koo, Goh and Tan2010) proposed a new evolutionary approach based on prediction to be applied during the change of environment. Based on the historic of previous solutions, the approach attempts to predict the direction and magnitude of the next environment change using the weighted average of these solutions. Updated individuals will remain in the vicinity of the new Pareto Front Pool and will help the rest of the population to converge. The algorithm known as population prediction strategy (PPS) (Zhou et al., Reference Zhou, Jin and Zhang2014) was presented in 2014 for continuous DMOPs. It tries to predict the entire population instead of forecasting some isolated points. It consists of dividing the set of solutions into two parts: central point and collectors. When the environment changes, the next central point is predicted using the sequence of central points found during the search, and the previous collectors are used to predict the next collectors. Thus, the PPS initializes the population by combining the central points and the collectors. Muruganantham et al. (Reference Muruganantham, Tan and Vadakkepat2016) proposed in 2015 a dynamic multiobjective evolutionary algorithm that uses the Kalman filter (Zai et al., Reference Zai, DeMarco and Lipo1992) as a prediction model. When the environment changes, the Kalman filter is applied to the population directing the search to the new Pareto Front in the objective space. This algorithm is based on the MOEA with Decomposition based on Differential Evolution (MOEA/D-DE) (Li and Zhang, Reference Li and Zhang2008) and is called the Kalman Filter prediction based DMOEA (MOEA/D-KF). In 2019, Cao et al. (Reference Cao, Xu, Goodman and Li2019) presents a new prediction model combined with a MultiObjective Evolutionary Algorithm based on Decomposition (MOEA/D) (Zhang and Li, Reference Zhang and Li2007) to solve DMOPs. In this model, the movement of the Pareto set over time is represented with respect to the translation of the centroid, and the other solutions are considered to have the same movement as the centroid. A prediction model is built based on the historic locations of recent centroids, which is used to estimate the centroid movement in the next environment change. Then, the new locations of the other solutions are also predicted based on their current locations. According to the authors, the model proposed in (Cao et al., Reference Cao, Xu, Goodman and Li2019) is based on two other works previously cited here (Koo et al., Reference Koo, Goh and Tan2010; Zhou et al., Reference Zhou, Jin and Zhang2014).
(iii) Memory: An algorithm was proposed in 2009 by Wang and Li (Reference Wang and Li2009) to solve dynamic multiobjective problems. It was called the multi-strategy ensemble MOEA (MS-MOEA) and it is one of the MOEAs investigated in the present work. In this algorithm, convergence is accelerated using a new generation dependency mechanism based on adaptive genetics and differential operators. It uses a Gaussian mutation and a memory-like strategy to reinitialize the population. In 2017, Azzouz et al. (Reference Azzouz, Bechikh and Said2017) presented an algorithm to deal with DMOPs with very severe changes. They introduced an adaptive hybrid population management strategy using memory and a random method to deal efficiently with dynamic environments. The Dynamic MultiObjective Evolutionary Algorithm Based on a Dynamic Evolutionary Environment model (DEE-DMOEA) was proposed by Zou in 2019 (Zou et al., Reference Zou, Li, Yang, Zheng, Peng and Pei2019). The algorithm records the evolutionary information generated to guide the search process. When the environment changes, the algorithm assists in the adaptation of the population to the new environment, building a dynamic evolutionary model that increases the diversity of the population. In 2020, Hu et al. (Reference Hu, Zheng, Zou, Yang, Ou and Wang2020) presented a new evolutionary algorithm based on the Intensity of Environmental Change (IEC). The algorithm divides each individual into two parts based on the feedback of the evolutionary information of the Pareto sets in the current and previous environments. The micro and macro-change decision components are implemented considering different scenarios, in order to build an efficient information exchange between dynamic environments.
The majority of DMOP algorithms are based on single-population frameworks. However, some multi-populational MOEAs have also been investigated. Goh and Tan (Reference Goh and Tan2009) presented in 2009 a co-evolutionary multiobjective algorithm based on competitiveness and cooperation to solve DMOPs. Aiming to overcome the difficulty of the decomposition problem and the interdependencies of the subcomponents resulting from co-EAs, the problem is decomposed into several subcomponents along the decision variables. These subcomponents are optimized by different sub-populations in the iterative process that involves competitiveness and cooperation. The algorithm is known as dynamic Competitive Cooperative EA (dCOEA). In 2013, Shang et al. (Reference Shang, Jiao, Ren, Li and Wang2013) proposed the quantum immune clonal co-evolutionary algorithm (QICCA) to solve DMOPs. QICCA is a multi-population algorithm using the strategies Immune Clonal Function and Clonal Selection generally applied to artificial immune systems (Shang et al., Reference Shang, Jiao, Gong and Lu2005). The relationship of competitiveness and cooperation are used to improve the exchange of information between populations, encouraging a better diversity in the search process. D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) is one of the MOEAs investigated in this paper and it is described in next section. It is a multi-population model based on MEANDS (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016), previously proposed for static MOPs, which employs both introduction to diversity and memory strategies to deal with environmental changes.
D-MEANDS-MD is a variation of D-MEANDS proposed in the present paper and it can also be classified as a multipopulational MOEA using introduction to diversity and memory strategies whenever a environmental change happens. As we have pointed in the introduction, the present work and the previous ones (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) are, to the best of our knowledge, the first that investigate EAs for dynamic many-objective problems (DMaOPs). However, it is worth to say that the authors in (Koo et al., Reference Koo, Goh and Tan2010) investigated test functions with 2 and 5 objectives. But, on the contrary of the present work, their investigation were totally based on a traditional multiobjective perspective and they did not stick to particular aspects of problems with many-objective formulations.
4. Investigated MOEAs
All the algorithms used in the experiments reported in Section 5 are briefly described here and the new proposal D-MEANDS-MD is also presented.
4.1. DNSGA-II*
The Dynamic Nondominated Sorting Genetic Algorithm II (DNSGA-II) (Deb and Karthik, Reference Deb and Karthik2007) is an adaptation of the well-known NSGA-II algorithm proposed by Deb and colleagues (Deb et al., Reference Deb, Pratap, Agarwal and Meyarivan2002). This variation was adapted in (Deb and Karthik, Reference Deb and Karthik2007) for dynamic problems using a strategy to introduce diversity whenever the environment used to evaluate the solutions faces some perturbation. The typical evolutionary behavior of NSGA-II was kept for DNSGA-II, except when an environment change happens. It consists of dividing the population into hierarchical fronts, where a solution from an upper front has a better fitness than another solution from a lower front. The fronts are classified based on the concept of Pareto dominance, where a solution that is not dominated by any other would be classified on the uppermost front. They are called the nondominated solutions of the current population and the goal is to approximate this uppermost front to the Pareto Optimum at the end of any arbitrary run. The other solutions are classified in a hierarchy of fronts where the solutions of an upper front dominates the solutions of lower fronts. The crowding distance metric is used to differentiate the solutions of the same front. This distance gives a better fitness for the solutions that are more isolated in the front.
In the DNSGA-II framework, a percentage of the current population is modified to promote diversity whenever the environment changes. Two strategies for this modification were evaluated in DNSGA-II (Deb and Karthik, Reference Deb and Karthik2007) defining different versions of this algorithm. The first version was called DNSGA-II-A, where a percentage of the population is kept intact for the next generation after the environment change (a kind of elitism) and other new individuals are generated at random replacing the worst solutions. The second version was called DNSGA-II-B, where the elitism was also used to keep a percentage of the best solutions while the new individuals that replace the worst ones are generated by applying mutation over the elite. The strategy used in the works (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) was DNSGA-II-A. Moreover, Lafetá and Oliveira proposed in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a) a change in DNSGA-II, where an external archive (Bosman and Thierens, Reference Bosman and Thierens2003) was introduced. The external archive stores all the nondominated solutions found in the population until the current generation, but it does not participate in the genetic operators selection. On that way, any nondominated solution is kept to end of the run, even if it disappears from the upper front due to size limit of the population. This strategy is very usual in different multiobjective models, like the MOEA/D (Zhang and Li, Reference Zhang and Li2007). This variation of the DNSGA-II algorithm was called DNSGA-II*. It was clear in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a) that DNSGA-II* outperforms DNSGA-II, with a little extra processing time.
4.2. MS-MOEA
The evolutionary process of the Multi-strategy Ensemble MOEA (MS-MOEA) (Wang and Li, Reference Wang and Li2010) is based on the concept of nondominance, as its population tends to maintain nondominated solutions and discards those that are dominated. Because the population has a fixed size, at the beginning of the search it is normal that not all individuals are nondominated. New nondominated descendants may be generated along the search and they replace the dominated individuals of the population. On the other way, if the current population does not have dominated individuals, the substitution is made at random. Since some nondominated solutions can be removed from the population, the algorithm stores all nondominated solutions found during the search in an internal archive. As this archive participates in the evolutionary process providing solutions to some matings, it is not considered an external archive like the one applied to DNSGA-II*. At ever change of environment some solutions stored in the archive suffer mutation and the new individuals are inserted in the population for the next environment. However, only a part of the population is made using mutation of the nondominated solutions found in the previous environment. The rest of the population of the new environment is generated randomly.
4.3. DDIS-MOEA/D-DE
The MOEA/D based on differential evolution and dynamic diversity introduction strategy (DDIS-MOEA/D-DE) (Liu et al., Reference Liu, Peng, Liu and Liu2020) is an algorithm for dynamic multiobjective problems that uses the same evolutionary process as MOEA/D-DE (Li and Zhang, Reference Li and Zhang2008), proposing a dynamic adaptive strategy according to the severity of change. MOEA/D-DE is an evolutionary multiobjective algorithm that decomposes the problem into several subproblems, which are evolved simultaneously. The decomposition is made by a scalarization function, which has the role of transforming each individual in a single scalar value (fitness). The current population is made up of the best solutions for each subproblem. The neighborhood of each subproblem is defined based on the distances between their weighting coeficient vectors. It is very important to highlight that the MOEA/D-DE uses differential evolution operators. The operators for genetic algorithms used in this paper were proposed (Tasgetiren et al., Reference Tasgetiren, Pan, Kizilay and Suer2015). Tasgetiren et al. (2015) proposed a model of differential evolution operators for the DMKP using a probability model based on the sigmoid function inspired by (Wang and Zheng, Reference Wang and Zheng2013). The main idea is to employ variable mutation strategies combined with a uniform crossover to generate a trial individual. The DDIS-MOEA/D-DE uses two strategies to create population during the change of environment. The first strategy occurs when the severity of change is high, so the algorithm takes advantage of the population from the previous environment and replaces part of the population with random individuals. However, when the severity of change is small, the algorithm keeps the population of the previous environment and applies a mutation in part of this population. In the experiments, the environment changes are controlled to keep the severity of change as low as possible, so the second strategy is always used. The number of individuals that mutate during the change of environment is equivalent to 20% of the population, as used in (Liu et al., Reference Liu, Peng, Liu and Liu2020).
4.4. D-MEANDS
DMEANDS is strongly based on its predecessor MEANDS. The Many-objective Evolutionary Algorithm Based on Nondominated Decomposed Sets (MEANDS) (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016) was proposed aimed at discrete and static MaOPs. The MEANDS framework manipulates several sub-populations (or subsets) of nondominated solutions. Each sub-population assesses the nondominance of individuals based on a subset of objectives. MEANDS initializes its population by generating a sample of random individuals of size A and verifying the dominance relation to insert the nondominated solutions into each subset considering the group of objectives related to each subpopulation. The insertion and removal process of individuals in each subset are independent because each subpopulation uses a different group of objectives. Each subset stores only nondominated solutions extracted from the random sample. For that, each individual x of the sample is sequentially evaluated and it is inserted in the subset when it is not dominated by any other individuals. Besides, if x dominates some other solution y previously inserted in the subset, then y is removed from this subpopulation. Therefore, during the population initialization, despite starting this process by generating a sample with A individuals, not all of them will survive. Each subset stores the current Pareto Front related to its group of objectives and the algorithm works with only first front solutions found for the subproblem related to these objectives. Each new individual generated by crossover is tested to be inserted into all the subsets. For each subset, the dominance is evaluated to decide the inclusion (or not) according to the respective group of objectives. This is the main reason that MEANDS generates only one individual per generation. Besides, each subset is scored according to its contribution to the search process (convergence score). The highest-scoring subsets participate more often in the crossover process. The convergence score is reset at each 100 generations to avoid stagnation. The parent selection has two steps, choosing two subsets and then choosing an individual from each one. The subset is selected by a tournament based on the convergence score and the individual is selected at random from each selected subset. The size of each subset is unlimited and it does not allow to insert duplicate individuals. Figure 1 shows the flowchart of the MEANDS algorithm.
The Dynamic Many-objective Evolutionary Algorithm Based on Nondominated Decomposed Sets (D-MEANDS) (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) was later proposed to deal with dynamic many-objective problems (DMaOPs). The adaptation made to manipulate dynamic MOPs is that, in the occurrence of changes in the environment, the individuals in the subset related to the set of all objectives - known as archive - are used to repopulate the new subsets. Note that not all individuals extracted from the archive of the previous environment will be reinserted in the new subsets. It depends on the nondominance of each old solution related to the subset of objectives considered in each sub-population. Besides, random individuals are also generated to repopulate the subsets considering the new environment objectives.

Figure 1. Flowchart: evolutionary strategy of MEANDS
4.5. D-MEANDS-MD
The Dynamic Many-objective Evolutionary Algorithm Based on Nondominated Decomposed Sets with Memory and Diversity (D-MEANDS-MD) uses the basic framework of MEANDS (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016), including the repopulation strategy used in D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) when the environment faces some change. Therefore, D-MEANDS-MD employs a subjacent structure of subsets (or sub-populations) of nondominated solutions. Each sub-population stores the nondominated solutions found by evolutionary process when just a related subset of objectives is considered. For example, in a problem with 4 objectives, each nondominated set is related to one of the possible combinations of a subset of objectives (two by two and three by three) and the last one considers all the 4 objectives. The dominance in each subset is based on the set of objectives for what it refers. The current population corresponds to the union of the nondominated solutions stored in all these sub-populations. The population is initialized with a sample of random individuals of size A, where each individual could be inserted in each subset depending to the nondominance in respect to the current solutions. The individuals with the worst genetic information probably will not be included in any subset. The set that uses all the objectives to define the dominance relation is called archive, because it has a behavior similar to the external archive used in several MOEAs. However, the archive participates of the evolutionary process.
D-MEANDS-MD employs a crossover based on the degree of convergence (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016), which generates a single child. In each generation, only one crossover occurs and each descendant generated is tested to be stored in each subset, depending on the respective dominance relation. During the attempt to insert the new descendant, if it is a nondominated solution for the respective subset, it removes the solutions that are dominated by it. In this way some current individuals can be removed during the insertion of a new one. Each sub-population has no size limitation and is classified by a score called the degree of convergence, where the best classified subsets have evolved more than other sets. That is, the sub-populations that have received more inclusions of new individuals in the last generations will receive a greater grade named degree of convergence. This degree is used in the crossover process divided in two stages. First, it selects two distinct sub-populations, where the selection of each one is based on the tournament-4 using the degree of convergence. Second, a parent individual is randomly selected in each subset. In order to prevent the algorithm from becoming biased in choosing the same group of subsets, the degree of convergence is restarted every 100 generations. Figure 2 shows the pseudocode of the proposed D-MEANDS-MD.

Figure 2. Pseudocode of D-MEANDS-MD
Similar to the adaptation incorporated in D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) to deal with dynamic optimization problems, when the environment faces any change, the population will be reinitialized but not exclusively at random. When the environment change happens, the individuals in the current archive, which considers all the objectives in the dominance relation, are used to repopulate all subsets of the new population. Therefore, this restocking strategy applied to the event of changes can be seen as a memory strategy, as it conserves part of the old population to start a new one. However, to inject some diversity into such changes, random individuals are also generated to repopulate the subsets considering the new environmental objectives. The number of random individuals is equal to the initial sample size A minus the number of nondominated solutions extracted from the previous environment.
In the previous D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) the diversity is applied only when the population resumes right after a disturbance of the environment. However, after our initial experiments using D-MEANDS reported in Section 5.1, it was possible to observe that when a high number of environment changes is employed, the convergence of the population based on the memory of the previous environment could not be as fast as the more dynamic problems need. In such cases, it proved important to inject some randomness over the generations between two changes. The new variation called D-MEANDS-MD employs a crossover with some degree of randomness, driven by a new balance parameter called as
![]() $B_{MD}$
. Each crossover has a
$B_{MD}$
. Each crossover has a
![]() $B_{MD}$
percentual chance of being employed exactly like D-MEANDS. Otherwise, a new individual is built at random to be the second parent of crossover. All the experiments in this paper uses
$B_{MD}$
percentual chance of being employed exactly like D-MEANDS. Otherwise, a new individual is built at random to be the second parent of crossover. All the experiments in this paper uses
![]() $B_{MD}$
=90%. Therefore, the proposed MOEA employs both memory and diversity strategies to balance the power of pre-existing nondominated individuals with the diversity of totally new individuals aiming to extract the best performance of the evolutionary search. Section 5.5 presents some experimental results showing the difference obtained when employing this degree of randomness (DMEANDS vs DMEANDS-MD). The percentual used in this balance (10% randomness and 90% memory) was empirically adjusted for the instances of the problem in tackle (DMKP). However,
$B_{MD}$
=90%. Therefore, the proposed MOEA employs both memory and diversity strategies to balance the power of pre-existing nondominated individuals with the diversity of totally new individuals aiming to extract the best performance of the evolutionary search. Section 5.5 presents some experimental results showing the difference obtained when employing this degree of randomness (DMEANDS vs DMEANDS-MD). The percentual used in this balance (10% randomness and 90% memory) was empirically adjusted for the instances of the problem in tackle (DMKP). However,
![]() $B_{MD}$
can be tunned for new scenarios or even for new dynamic problems.
$B_{MD}$
can be tunned for new scenarios or even for new dynamic problems.
5. Experiments
All the experiments reported here investigate the dynamic version of the multiobjective knapsack problem (DMKP), using formulations with 4–8 objectives. For each formulation, three instances of DMKP were evaluated, by varying the number of items to be packed. First, the behavior of the three published algorithms DNSGA-II*, MS-MOEA, and D-MEANDS was analyzed using dynamic scenarios that involve 10, 15 and 20 environments changes (ECs). The results and analysis over these experiments led us to propose the D-MEANDS-MD algorithm. Later, the performance of this novel algorithm was also analyzed. In order to evaluate the performance of the different MOEAs solving DMKP, two metrics were used: density (AD) and hypervolume (HV). Both are described as follows.
Density (AD) (Zhang and Qian, Reference Zhang and Qian2011): can be used to measure all the distribution performance of the nondominated solutions obtained by the MOEA in the environments. The lower the value of the metric, the better the distribution of the solutions.
 \begin{align}AD=\frac{1}{EC} \sum_{t=1}^{EC} \sqrt{\frac{1}{|A^{t}|-1} \sum_{j=1}^{|A^{t}|} (\bar{d^{t}} - d^{t}_j)^{2} }\end{align}
\begin{align}AD=\frac{1}{EC} \sum_{t=1}^{EC} \sqrt{\frac{1}{|A^{t}|-1} \sum_{j=1}^{|A^{t}|} (\bar{d^{t}} - d^{t}_j)^{2} }\end{align}
Where,
 \begin{align}d^{t}_j = \min_{k\neq j,1\leq k\leq |A^{t}|} \left \{ || f(x_{j}) - f(x_{k}) ||, (x_{j},x_{k}) \in A^{t} \right \}, \bar{d^{t}}=\frac{1}{|A^{t}|} \sum_{j=1}^{|A^{t}|} d^{t}_j\end{align}
\begin{align}d^{t}_j = \min_{k\neq j,1\leq k\leq |A^{t}|} \left \{ || f(x_{j}) - f(x_{k}) ||, (x_{j},x_{k}) \in A^{t} \right \}, \bar{d^{t}}=\frac{1}{|A^{t}|} \sum_{j=1}^{|A^{t}|} d^{t}_j\end{align}
Consider
![]() $A^{t}$
the Pareto found in the environment t; EC the number of environment changes;
$A^{t}$
the Pareto found in the environment t; EC the number of environment changes;
![]() $d^{t}_j$
represents the distance between j solution and another distinct solution in the population that is as close as possible in the environment t;
$d^{t}_j$
represents the distance between j solution and another distinct solution in the population that is as close as possible in the environment t;
Hypervolume (HV) (Zitzler and Thiele, Reference Zitzler and Thiele1998): The hypervolume measures the volume of the region covered between the points of the Pareto solutions found and a reference point. Mathematically, for each solution i belonging to the Pareto found, a hypercube is built according to a reference point
![]() $W_0$
. The sum of the volume of these hypercubes returns the hypervolume. The point
$W_0$
. The sum of the volume of these hypercubes returns the hypervolume. The point
![]() $W_0$
used in this work is the point of origin of the dimensions. The metric evaluates convergence and diversity. The algorithm with the highest HV value indicates better convergence and diversity than the other algorithms.
$W_0$
used in this work is the point of origin of the dimensions. The metric evaluates convergence and diversity. The algorithm with the highest HV value indicates better convergence and diversity than the other algorithms.
After analyzing the results of the two metrics, it was possible to observe that they approximate to a Gaussian distribution. In addition, we apply a sample size of 100 tests in all experiments. Thus, a hypothesis test T (Mankiewicz, Reference Mankiewicz2000) was used to assess the significant difference between the performance of the algorithms. In addition, we evaluate the execution time of them.
We used 27 DMKP instances in the experiments, which are divided by the number of items, objectives and environment changes (EC). In the present paper, we used 30, 50 and 100 items with 4, 6, and 8 objectives. The changes in environments ranged from 10, 15, and 20. We use the following parameters for the
![]() $DNSGA-II^*$
and MS-MOEA: 500 generations, 100% crossover, 10% mutation, population size = 100. For
$DNSGA-II^*$
and MS-MOEA: 500 generations, 100% crossover, 10% mutation, population size = 100. For
![]() $DNSGA-II^*$
, 20% of the population has been replaced at each environment change. In MS-MOEA, at each change of environment, 20% of the population is made up of individuals from the archive that has been mutated and 80% are random individuals. Since D-MEANDS performs only one crossover per generation, its parameters were chosen to perform the same number of crossovers as the other algorithms, which are: 50 000 generations, 10% mutation and 1000 individuals used to initialize the population. Each algorithm was executed 100 times for each instance. Graphs show the average and standard deviation of these 100 executions considering each performance metric and execution time.
$DNSGA-II^*$
, 20% of the population has been replaced at each environment change. In MS-MOEA, at each change of environment, 20% of the population is made up of individuals from the archive that has been mutated and 80% are random individuals. Since D-MEANDS performs only one crossover per generation, its parameters were chosen to perform the same number of crossovers as the other algorithms, which are: 50 000 generations, 10% mutation and 1000 individuals used to initialize the population. Each algorithm was executed 100 times for each instance. Graphs show the average and standard deviation of these 100 executions considering each performance metric and execution time.
All algorithms were implemented here using the JAVA language and they were executed on the same machine with the following configuration: Dell Inspiron 3647 microprocessor; CPU: Intel Core i5 (4th generation); RAM: 8GB DDR3 1600MHz; OS: Windows 8.1.
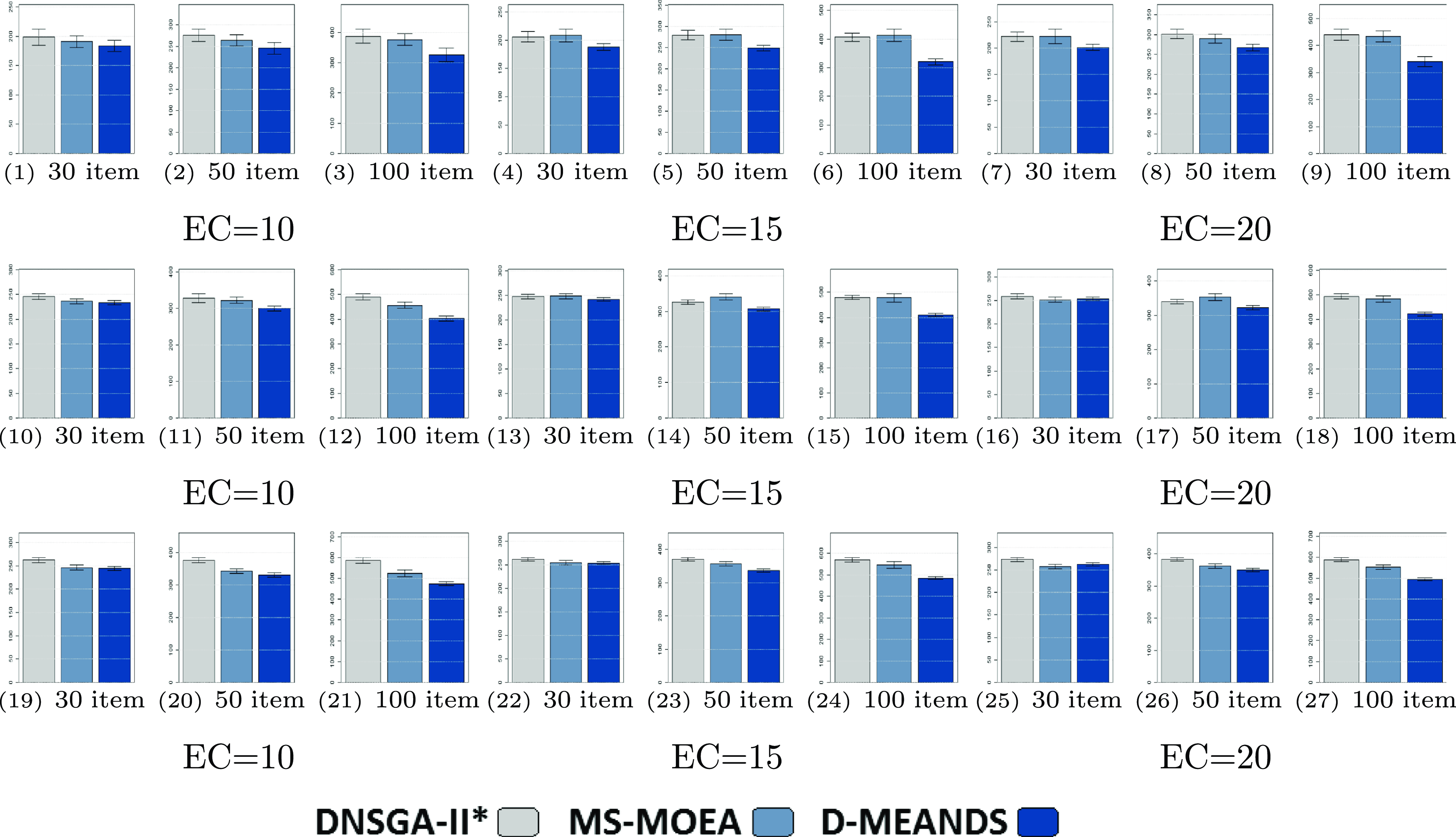
Figure 3. Density results (AD). The figures from (1) to (9) are the results of 4 objectives. The figures from (10) to (18) are the results of 6 objectives. The figures from (19) to (27) are the results of 8 objectives
5.1. Experiments using
 $DNSGA-II^*$
, MS-MOEA and D-MEANDS
$DNSGA-II^*$
, MS-MOEA and D-MEANDS
In this section, the performance of the three algorithms investigated in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) are evaluated using a number of environment changes and a number of objectives higher than that previously used. Lafetá and Oliveira showed that the increase in the number of environment changes made DNSGA-II considerably improves its results compared with the other two algorithms. However, the instances were limited to only 4 objectives when 10 environment changes were employed. This limitation was made mainly due to the employment of parametric metrics that greatly increased the computational cost. On the other hand, since non-parametric metrics are used in the present work, it enabled us to analyze the behavior of these algorithms in more complex scenarios up to instances with 8 objectives and 20 environment changes.
Figure 3 shows the results of the AD metric for all the 27 scenarios. As can be noted, D-MEANDS has the best values in almost all instances. The exceptions are three scenarios with 30 items: one involving 6 objectives (EC=15) and two with 8 objectives (EC=15 and EC=20). Even in these 3 scenarios D-MEANDS found results similar to the best found by MS-MOEA. By comparing MS-MOEA and
![]() $DNSGA-II^*$
, the second outperforms the first in some instances (eight of them), but MS-MOEA is better than
$DNSGA-II^*$
, the second outperforms the first in some instances (eight of them), but MS-MOEA is better than
![]() $DNSGA-II^*$
in the most of the 27 scenarios. Based on AD results, it is possible to conclude that D-MEANDS finds more distributed sets of solutions.
$DNSGA-II^*$
in the most of the 27 scenarios. Based on AD results, it is possible to conclude that D-MEANDS finds more distributed sets of solutions.
Figure 4 shows the HV metric results. In 9 out of the 27 instances, the
![]() $DNSGA-II^*$
outperforms the other algorithms. These scenarios use 4 or 6 objectives. However, in the majority of scenarios (including all the 9 scenarios with 8 objectives), D-MEANDS achieved the best performance. It was possible to notice that the increased number of objectives highlights D-MEANDS performance. On the other hand, it can also be observed that the increased number of environment changes decays D-MEANDS metrics in respect to the other MOEAs. Moreover, the increment of items to be packed also contributes to the decay on D-MEANDS performance. Comparing MS-MOEA and
$DNSGA-II^*$
outperforms the other algorithms. These scenarios use 4 or 6 objectives. However, in the majority of scenarios (including all the 9 scenarios with 8 objectives), D-MEANDS achieved the best performance. It was possible to notice that the increased number of objectives highlights D-MEANDS performance. On the other hand, it can also be observed that the increased number of environment changes decays D-MEANDS metrics in respect to the other MOEAs. Moreover, the increment of items to be packed also contributes to the decay on D-MEANDS performance. Comparing MS-MOEA and
![]() $DNSGA-II^*$
, the first outperforms the later in most HV results.
$DNSGA-II^*$
, the first outperforms the later in most HV results.
The T-test (Mankiewicz, Reference Mankiewicz2000) was used to assess the significance of the D-MEANDS performance compared with the others and the results are shown in Tables 1, 2, and 3. This hypothesis test was done with 99% confidence. Each row of the tables represents the comparison of D-MEANDS with other algorithm and that the column indicates the metric. Green cells show that D-MEANDS was significantly higher and red cells show it was significantly lower. In white, there was no significant difference. We can see the results in Table 1 for instances with EC=10. Tables 2 and 3 show similar results for EC=15 and EC=20, respectively. The hypothesis test confirms that there are significant evidences of the superiority of D-MEANDS in AD metric in almost all scenarios and that, in general, D-MEANDS returns a better performance in HV metric.
The execution time of the algorithms is shown in Figure 5. Clearly, the
![]() $DNSGA-II^*$
processing time is much lower than the other algorithms. This observation becomes more evident with the increasing complexity of the instances. D-MEANDS has an execution time close to that of
$DNSGA-II^*$
processing time is much lower than the other algorithms. This observation becomes more evident with the increasing complexity of the instances. D-MEANDS has an execution time close to that of
![]() $DNSGA-II^*$
in the instances of 4 objectives, but as the number of objectives increases, its execution time increases much more than
$DNSGA-II^*$
in the instances of 4 objectives, but as the number of objectives increases, its execution time increases much more than
![]() $DNSGA-II^*$
. D-MEANDS processing time is shorter than that of MS-MOEA in all instances of 4 and 6 objectives but they are close when formulations with 8 objectives were used (D-MEANDS is still faster in about half of scenarios).
$DNSGA-II^*$
. D-MEANDS processing time is shorter than that of MS-MOEA in all instances of 4 and 6 objectives but they are close when formulations with 8 objectives were used (D-MEANDS is still faster in about half of scenarios).
D-MEANDS found better AD and HV results in most instances. It also scales better when the number of objectives is increased up to 8. However, as we increase the number of environment changes (EC) and the number of items to be packed, which represents more difficult instances, D-MEANDS performance decays when compared with the other algorithms. On the other hand,
![]() $DNSGA-II^*$
proved to be very competitive in some instances demanding a lower execution time, even when the number of objectives is increased.
$DNSGA-II^*$
proved to be very competitive in some instances demanding a lower execution time, even when the number of objectives is increased.

Figure 4. Hypervolume results (HV). The figures from (1) to (9) are the results of 4 objectives. The figures from (10) to (18) are the results of 6 objectives. The figures from (19) to (27) are the results of 8 objectives
Table 1. Hypothesis test T of the instances with EC=10. Comparing D-MEANDS vs All algorithms

Table 2. Hypothesis test T of the instances with EC=15. Comparing D-MEANDS vs All algorithms

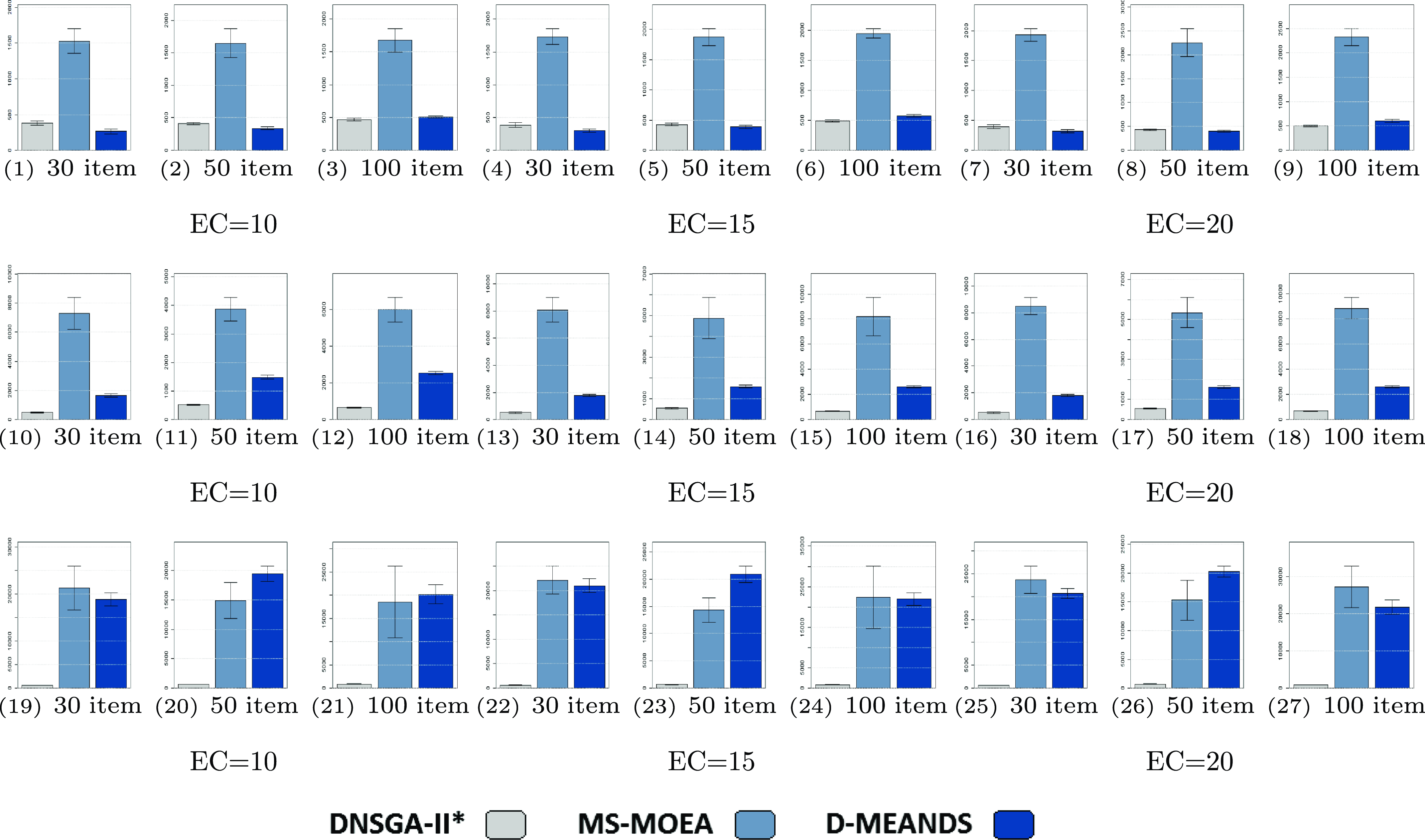
Figure 5. Time Execution. The figures from (1) to (9) are the results of 4 objectives. The figures from (10) to (18) are the results of 6 objectives. The figures from (19) to (27) are the results of 8 objectives
5.2. Experiments including D-MEANDS-MD
We investigated the possible causes for D-MEANDS performance decay when the number of environment changes are increased. It was possible to observe that in such scenarios, the convergence of this MOEA is not so fast as needed mainly because there is a severe decay in the variability of the nondominated solutions, since the basic MEANDS and D-MEANDS frameworks discard all the information of dominated solutions. Therefore, it becomes clear the need of a new mechanism to inject some randomness what led us to the proposition of D-MEANDS-MD explained in Section 4.5.
Table 3. Hypothesis test T of the instances with EC=20. Comparing D-MEANDS vs All algorithms

In this session, the proposal D-MEANDS-MD is confronted with the other MOEAs. From the previous section, we repeat the values of
![]() $DNSGA-II^*$
and D-MEANDS metrics to investigate the impact of the implemented modification in respect to the two best MOEAs, being that DNSGA-II has been evidenced by its lower computational time while D-MEANDS returned the best performance in AD and HV metrics. Moreover, we also implemented a variation of
$DNSGA-II^*$
and D-MEANDS metrics to investigate the impact of the implemented modification in respect to the two best MOEAs, being that DNSGA-II has been evidenced by its lower computational time while D-MEANDS returned the best performance in AD and HV metrics. Moreover, we also implemented a variation of
![]() $DNSGA-II^*$
called here
$DNSGA-II^*$
called here
![]() $DNSGA-II^+$
where the same diversity mechanism proposed for D-MEANDS-MD was incorporated. That is, 10% of crossover matings in
$DNSGA-II^+$
where the same diversity mechanism proposed for D-MEANDS-MD was incorporated. That is, 10% of crossover matings in
![]() $DNSGA-II^+$
use a random parent. In Table 4 we can see the parameters used by D-MEANDS and D-MEANDS-MD.
$DNSGA-II^+$
use a random parent. In Table 4 we can see the parameters used by D-MEANDS and D-MEANDS-MD.
Table 4. D-MEANDS and D-MEANDS-MD parameters

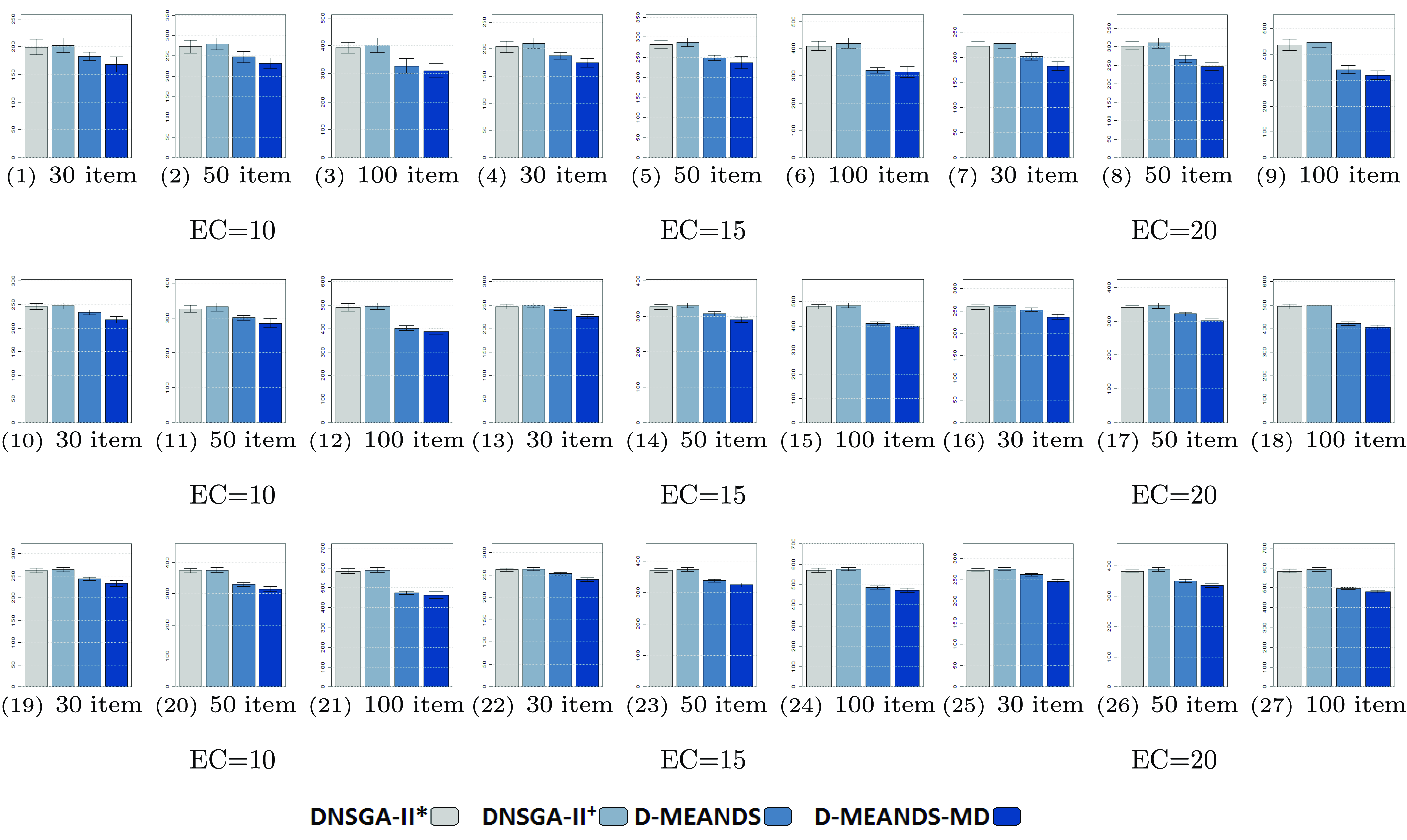
Figure 6. Diversity results (AD). The figures from (1) to (9) are the results of 4 objectives. The figures from (10) to (18) are the results of 6 objectives. The figures from (19) to (27) are the results of 8 objectives
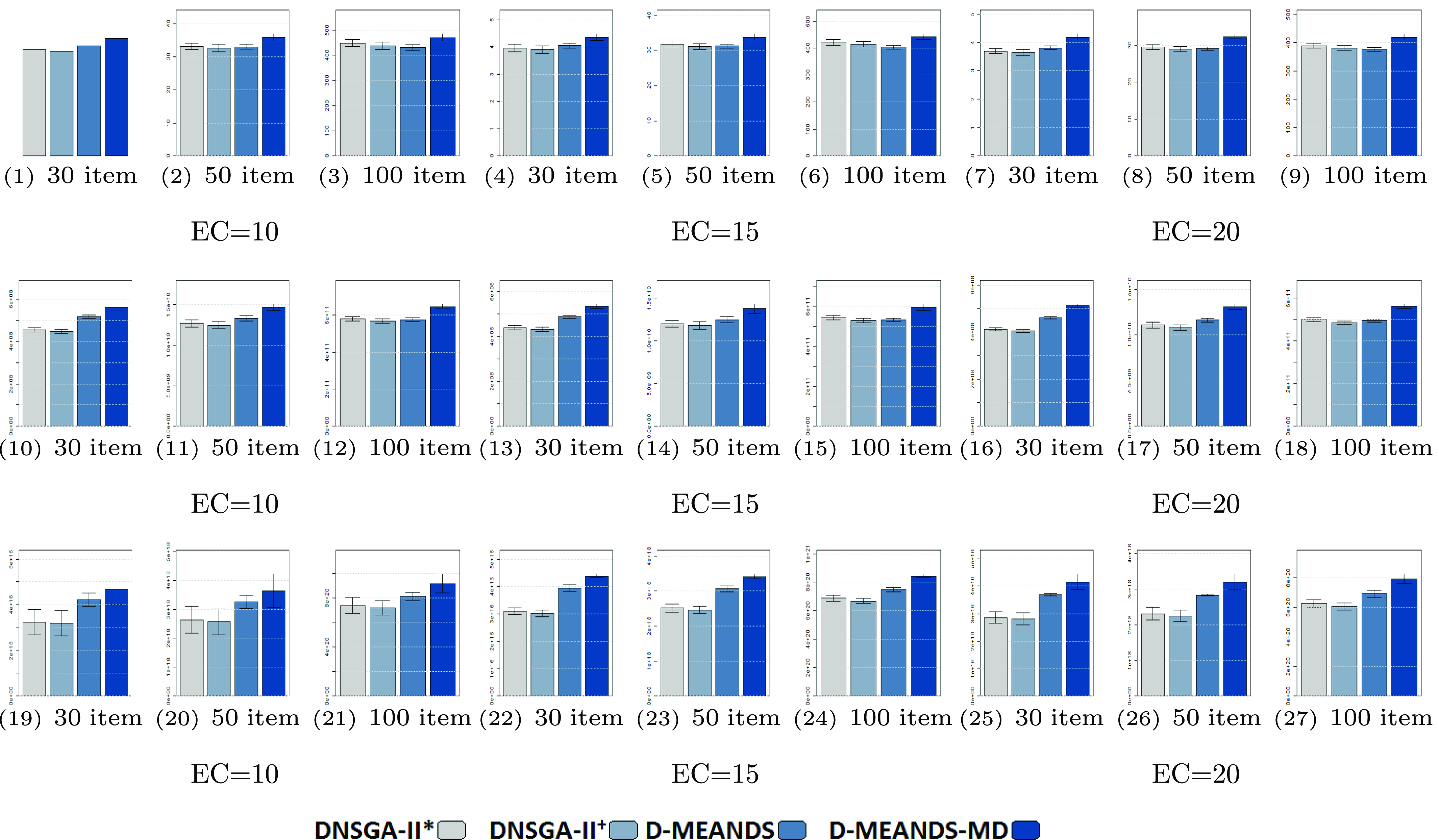
Figure 7. Hypervolume results (HV). The figures from (1) to (9) are the results of 4 objectives. The figures from (10) to (18) are the results of 6 objectives. The figures from (19) to (27) are the results of 8 objectives
Figure 6 shows the results related to AD metric: D-MEANDS-MD performed better than all the other algorithms, followed by the original D-MEANDS performance.
![]() $DNSGA-II^+$
showed no improvement compared with
$DNSGA-II^+$
showed no improvement compared with
![]() $DNSGA-II^*$
. Analyzing the results of the HV metric in Figure 7, D-MEANDS-MD overcame all the other algorithms, followed by D-MEANDS performance. As observed with the other metric,
$DNSGA-II^*$
. Analyzing the results of the HV metric in Figure 7, D-MEANDS-MD overcame all the other algorithms, followed by D-MEANDS performance. As observed with the other metric,
![]() $DNSGA-II^+$
showed no improvement compared with
$DNSGA-II^+$
showed no improvement compared with
![]() $DNSGA-II^*$
.
$DNSGA-II^*$
.
Table 5. Hypothesis test T of the instances with EC=10. Comparing D-MEANDS-MD vs All algorithms

Table 6. Hypothesis test T of the instances with EC=15. Comparing D-MEANDS-MD vs All algorithms

Table 7. Hypothesis test T of the instances with EC=20. Comparing D-MEANDS-MD vs All algorithms
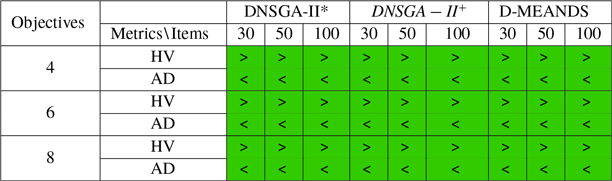
Therefore, the introduction of a randomness mechanism is
![]() $DNSGA-II^*$
did not return any significant improvement. On the other hand, this mechanism had a positive robust impact on D-MEANDS. The D-MEANDS-MD proposal improved the results of all instances in both metrics. As a consequence, the new algorithm overcame all the other algorithms.
$DNSGA-II^*$
did not return any significant improvement. On the other hand, this mechanism had a positive robust impact on D-MEANDS. The D-MEANDS-MD proposal improved the results of all instances in both metrics. As a consequence, the new algorithm overcame all the other algorithms.
The T-test was used to assess the significance of D-MEANDS-MD results compared with the others. This hypothesis test was done with 99% confidence and one can see the results in Tables 5, 6, and 7 for instances with EC=10, EC=15, and EC=20, respectively. Each row of the table represents the comparison of D-MEANDS-MD with other algorithm and the column indicates the metric. It is possible to observe that the proposal D-MEANDS-MD significantly outperforms all the other algorithms in all 27 investigated instances.
Figure 8 shows the processing time related to each investigated MOEA. D-MEANDS and D-MEANDS-MD were faster than the
![]() $DNSGA-II^*$
and
$DNSGA-II^*$
and
![]() $DNSGA-II^+$
in some instances using 4 objectives. But when using formulations with 6 or 8 objectives,
$DNSGA-II^+$
in some instances using 4 objectives. But when using formulations with 6 or 8 objectives,
![]() $DNSGA-II^*$
and
$DNSGA-II^*$
and
![]() $DNSGA-II^+$
are clearly faster. The increase in the number of objectives shows that D-MEANDS-MD takes a longer processing time than D-MEANDS. However, D-MEANDS-MD execution time proved to be similar to D-MEANDS: it has a much greater increase in processing time than the two algorithms
$DNSGA-II^+$
are clearly faster. The increase in the number of objectives shows that D-MEANDS-MD takes a longer processing time than D-MEANDS. However, D-MEANDS-MD execution time proved to be similar to D-MEANDS: it has a much greater increase in processing time than the two algorithms
![]() $DNSGA-II^*$
and
$DNSGA-II^*$
and
![]() $DNSGA-II^+$
as we increase the number of objectives. Therefore, although D-MEANDS-MD showed the best performance in terms of multiobjective metrics, it is as time expensive as its precursor D-MEANDS.
$DNSGA-II^+$
as we increase the number of objectives. Therefore, although D-MEANDS-MD showed the best performance in terms of multiobjective metrics, it is as time expensive as its precursor D-MEANDS.
Additionally, we speculated if
![]() $DNSGA-II^*$
would achieve better results than D-MEANDS and D-MEANDS-MD if have extra time to perform its evolutionary search. Aiming to answer this question we ran extra experiments, in which we increased the number of generations of
$DNSGA-II^*$
would achieve better results than D-MEANDS and D-MEANDS-MD if have extra time to perform its evolutionary search. Aiming to answer this question we ran extra experiments, in which we increased the number of generations of
![]() $DNSGA-II^*$
. For instances of 30 items, we multiply by 5 the number of generations of
$DNSGA-II^*$
. For instances of 30 items, we multiply by 5 the number of generations of
![]() $DNSGA-II^*$
, for 50 items we multiply by 10 and for 100 items we multiply by 40. With such increased number of generations, in all instances DNSGA-II* surpassed the execution time of the other two algorithms. We redid the experiments of this section comparing
$DNSGA-II^*$
, for 50 items we multiply by 10 and for 100 items we multiply by 40. With such increased number of generations, in all instances DNSGA-II* surpassed the execution time of the other two algorithms. We redid the experiments of this section comparing
![]() $DNSGA-II^*$
with D-MEANDS and D-MEANDS-MD, while the parameters of D-MEANDS and D-MEANDS-MD are kept fixed. Due to lack of space, we did not include these new results here. However, we could confirm that
$DNSGA-II^*$
with D-MEANDS and D-MEANDS-MD, while the parameters of D-MEANDS and D-MEANDS-MD are kept fixed. Due to lack of space, we did not include these new results here. However, we could confirm that
![]() $DNSGA-II^*$
did not surpass D-MEANDS and D-MEANDS-MD in AD and HV metrics even using extra processing time.
$DNSGA-II^*$
did not surpass D-MEANDS and D-MEANDS-MD in AD and HV metrics even using extra processing time.
5.3. Experiments including DDIS-MOEA/D-DE
Aiming at comparing D-MEANDS-MD and a more recent algorithm in the literature, a new experiment was carried out. The DDIS-MOEA/D-DE presented in Section 4.3, uses the same evolutionary strategy as the MOEA/D-DE with a dynamic strategy based on diversity. The chosen algorithm was proposed recently and according to the authors in (Liu et al., Reference Liu, Peng, Liu and Liu2020) has returned good results in a controlled and continuous dynamic environment. The following parameters were used in DDIS-MOEA/D-DE: 500 generations, 100% crossover, 10% mutation, population size = 100, and 20% of its population mutates during the change of environment.
![]() $DNSGA-II^+$
and D-MEANDS were also maintained in order to compare the performance of DDIS-MOEA/D-DE with another algorithm that uses dynamic strategy based on diversity (
$DNSGA-II^+$
and D-MEANDS were also maintained in order to compare the performance of DDIS-MOEA/D-DE with another algorithm that uses dynamic strategy based on diversity (
![]() $DNSGA-II^+$
) and the precursor of D-MEANDS-MD (D-MEANDS). In this experiment, only instances with EC=20 were considered.
$DNSGA-II^+$
) and the precursor of D-MEANDS-MD (D-MEANDS). In this experiment, only instances with EC=20 were considered.

Figure 8. Time Execution. The figures from (1) to (9) are the results of 4 objectives. The figures from (10) to (18) are the results of 6 objectives. The figures from (19) to (27) are the results of 8 objectives
Figure 9 shows the AD metric achieved by each DMOEA in the investigated scenarios. DDIS-MOEA/D-DE presents worse results than
![]() $DNSGA-II^*$
, DMEANDS and DMEANDS-MD in all instances. In Figure 10 we can see the results of the HV metric, where the DDIS-MOEA/D-DE also presents the worst results in all instances compared with the other algorithms. The execution time of the algorithms is shown in Figure 11. As observed in the last section, D-MEANDS and D-MEANDS-MD significantly worsen their execution time as the number of objectives increases. For 4 and 6 objectives, both algorithms get a shorter time than DDIS-MOEA/D-DE, but they demand more processing time with 8 objectives. Thus, we can see that DDIS-MOEA/D-DE presents a better behavior than DMEANDS and DMEANDS-MD in respect to the execution time as the number of objectives increases. However, when compared with
$DNSGA-II^*$
, DMEANDS and DMEANDS-MD in all instances. In Figure 10 we can see the results of the HV metric, where the DDIS-MOEA/D-DE also presents the worst results in all instances compared with the other algorithms. The execution time of the algorithms is shown in Figure 11. As observed in the last section, D-MEANDS and D-MEANDS-MD significantly worsen their execution time as the number of objectives increases. For 4 and 6 objectives, both algorithms get a shorter time than DDIS-MOEA/D-DE, but they demand more processing time with 8 objectives. Thus, we can see that DDIS-MOEA/D-DE presents a better behavior than DMEANDS and DMEANDS-MD in respect to the execution time as the number of objectives increases. However, when compared with
![]() $DNSGA-II^*$
it demands more processing time in all instances. Therefore, we can see that between the two algorithms that use dynamic strategy based on diversity,
$DNSGA-II^*$
it demands more processing time in all instances. Therefore, we can see that between the two algorithms that use dynamic strategy based on diversity,
![]() $DNSGA-II^*$
performed better in DMKP.
$DNSGA-II^*$
performed better in DMKP.

Figure 9. Diversity performance for instances with EC=20. Graphs from (1) to (3) show the results for 4 objectives. Graphs from (4) to (6) show the results for 6 objectives. Graphs from (7) to (9) show the results for 8 objectives
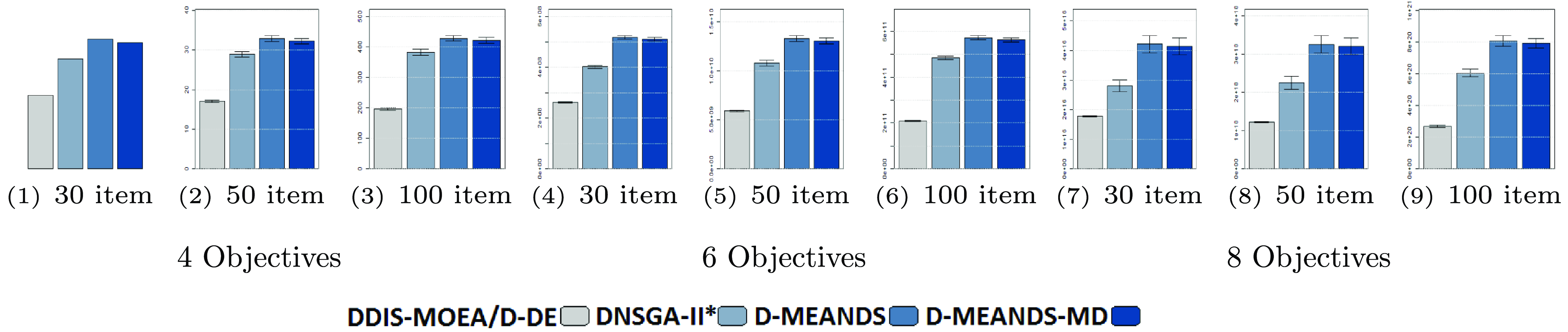
Figure 10. Hypervolume performance for instances with EC=20. Graphs from (1) to (3) show the results for 4 objectives. Graphs from (4) to (6) show the results for 6 objectives. Graphs from (7) to (9) show the results for 8 objectives
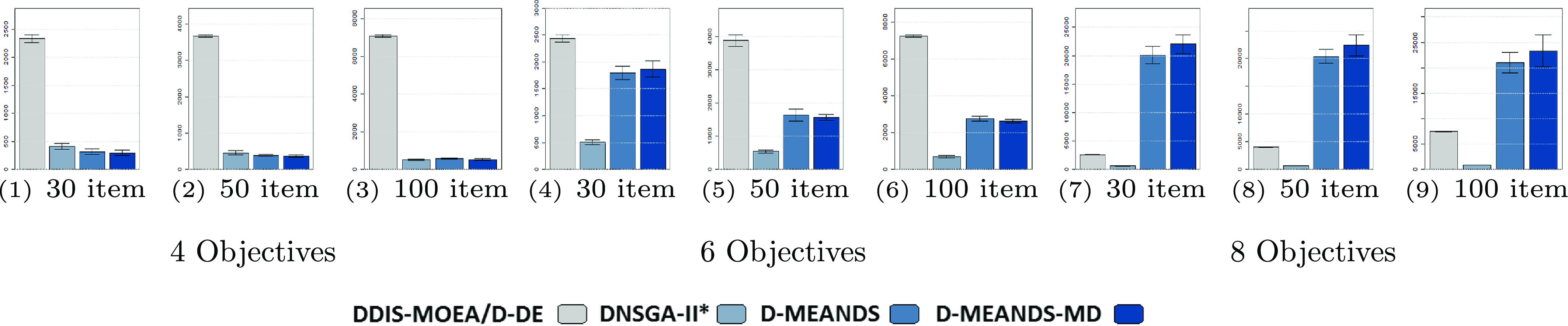
Figure 11. Time Execution performance for instances with EC=20. Graphs from (1) to (3) show the results for 4 objectives. Graphs from (4) to (6) show the results for 6 objectives. Graphs from (7) to (9) show the results for 8 objectives
Although not presented in the present paper, similar experiments were performed using the execution time as stop criteria (instead of number of generations). In such experiments, each execution stopped for a time limit of 30 seconds. The main conclusions were: (i) D-MEANDS-MD performed better in HV and AD metrics than the other MOEAs and (ii) D-MEANDS-MD and
![]() $DNSGA-II^*$
outperforms DDIS-MOEA/D-DE. However, in these supplementary experiments, we could not guarantee that all the algorithms were submitted to exactly the same number of environmental changes. In future investigations, we intend to implement a new framework for experiments where it will be able to compare the MOEAs with the same execution time and the same number of environmental changes.
$DNSGA-II^*$
outperforms DDIS-MOEA/D-DE. However, in these supplementary experiments, we could not guarantee that all the algorithms were submitted to exactly the same number of environmental changes. In future investigations, we intend to implement a new framework for experiments where it will be able to compare the MOEAs with the same execution time and the same number of environmental changes.
The T-test was used to assess the significance of D-MEANDS-MD performance compared with the other investigated algorithms. The test was done with 99% confidence and the results are presented in Table 8 for instances with EC=20. Each column of the table represents the comparison of D-MEANDS-MD with other algorithm with respect to number of the items, and the row indicates the metric and number of objectives considered. It is possible to note that the D-MEANDS-MD is significantly superior to the other algorithms in all instances.
Table 8. Hypothesis test T of the instances with EC=20. Comparing D-MEANDS-MD vs All algorithms
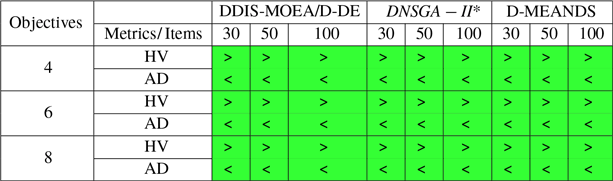
5.4. Analyzing the dominance of the final set of solutions
In the experiments reported in the last sections, the MOEAs were evaluated regarding AD and HV metrics, which give absolute values to make a comparison among several algorithms. These metrics translate some characteristics of the Pareto approximation found by a specific algorithm, such as diversity and convergence to Pareto Optimum, to numerical values that make these multiple comparison possible. However, its is common in multiobjective investigation, to perform a direct comparison of two algorithms regarding the quality of the set of solutions found by each one. In this section, the Coverage of two Sets (CS) metric is used to perform a direct comparison between the algorithms with the best performances on the last experiments:
![]() $DNSGA-II^*$
, D-MEANDs and D-MEANDS-MD.
$DNSGA-II^*$
, D-MEANDs and D-MEANDS-MD.
CS definition: (Zitzler, Reference Zitzler1999): Consider two Pareto sets X and Y. Function F evaluates the dominance relationship of Pareto X to Y, returning a value between 0 and 1. If
![]() $F=1$
means that all solutions of Y are dominated by some point of X, while
$F=1$
means that all solutions of Y are dominated by some point of X, while
![]() $F=0$
means that no solutions of Y are dominated by X. Note that it does not mean that there is some point of Y that dominates a solution of X. Formally, the CS metric is calculated as follow:
$F=0$
means that no solutions of Y are dominated by X. Note that it does not mean that there is some point of Y that dominates a solution of X. Formally, the CS metric is calculated as follow:
This experiment was performed using the scenarios with the higher number of changes, that is, using only EC=20 instances. Each result represents the mean of 100 comparisons between the Pareto set of two algorithms (X and Y). Tables 9, 10, and 11 present the values of the CS metric achieved using the DMOEAs in scenarios with 30, 50, and 100 items, respectively. The row represents the Pareto set X and the column represents the set Y. As closer the value is to 1, as more solutions of the column algorithm (Y) are dominated by solutions of the row algorithm (X). Each algorithm was represented by a lowercase letter: a=
![]() $DNSGA-II^*$
, b=D-MEANDS and c=D-MEANDS-MD. We can see in Table 9 (instances of 30 items),
$DNSGA-II^*$
, b=D-MEANDS and c=D-MEANDS-MD. We can see in Table 9 (instances of 30 items),
![]() $DNSGA-II^*$
finds very few solutions that dominate the solutions of D-MEANDS and D-MEANDS-MD. On the other hand, about 70% of the
$DNSGA-II^*$
finds very few solutions that dominate the solutions of D-MEANDS and D-MEANDS-MD. On the other hand, about 70% of the
![]() $DNSGA-II^*$
solutions are dominated by the DMEANS and D-MEANDS-MD solutions. Regarding D-MEANDS-MD and D-MEANDS the CS difference is not so evident (between 2% and 4%). However, in all scenarios D-MEANDS-MD have more solutions dominated by D-MEANDS than the opposite. In the instances of 50 (Table 10) and 100 items (Table 11), as the number of items increases, as more solutions of
$DNSGA-II^*$
solutions are dominated by the DMEANS and D-MEANDS-MD solutions. Regarding D-MEANDS-MD and D-MEANDS the CS difference is not so evident (between 2% and 4%). However, in all scenarios D-MEANDS-MD have more solutions dominated by D-MEANDS than the opposite. In the instances of 50 (Table 10) and 100 items (Table 11), as the number of items increases, as more solutions of
![]() $DNSGA-II^*$
are dominated by the other two algorithms (around 80% and 90% in all instances of 50 and 100 items, respectively). The performances of the D-MEANDS and D-MEANDS-MD are similar to that observed with 30 items. The difference in CS is not so evident between both D-MEANDS versions (up to 8% of difference). However, in all scenarios this slight difference favours D-MEANDS.
$DNSGA-II^*$
are dominated by the other two algorithms (around 80% and 90% in all instances of 50 and 100 items, respectively). The performances of the D-MEANDS and D-MEANDS-MD are similar to that observed with 30 items. The difference in CS is not so evident between both D-MEANDS versions (up to 8% of difference). However, in all scenarios this slight difference favours D-MEANDS.
Table 9. CS metric in instances of 30 items and EC=20, using a=
![]() $DNSGA-II^*$
; b=D-MEANDS; c=D-MEANDS-MD algorithms
$DNSGA-II^*$
; b=D-MEANDS; c=D-MEANDS-MD algorithms

Table 10. CS metric in instances of 50 items and EC=20, using a=
![]() $DNSGA-II^*$
; b=D-MEANDS; c=D-MEANDS-MD algorithms
$DNSGA-II^*$
; b=D-MEANDS; c=D-MEANDS-MD algorithms

Table 11. CS metric in instances of 100 items and EC=20, using a=
![]() $DNSGA-II^*$
; b=D-MEANDS; c=D-MEANDS-MD algorithms
$DNSGA-II^*$
; b=D-MEANDS; c=D-MEANDS-MD algorithms

The CS metric compares two multiobjective algorithms and gives us an idea of which one presents a better convergence to the Pareto Optimum. This is a relative result because it does not quantify the magnitude of this difference on convergence. Nevertheless, one can see that D-MEANDS presents a better convergence to Pareto than D-MEANDS-MD. Therefore, a question arose after obtaining these results: why is D-MEANDS-MD better in the HV metric than D-MEANDS, as showed in Section 5.2, if CS results show that D-MEANDS has a better convergence? We believe that the answer is related to the D-MEANDS-MD mechanism to increase diversity in the population (and indeed diversity is of great importance to dynamic problems). On the other hand, the hypervolume is influenced by both convergence and diversity, being that the greater the convergence and diversity of an algorithm, the better the value of HV. Therefore, we conclude that D-MEANDS-MD presents a better diversity and a worse convergence than D-MEANDS. However, we speculate that the difference in diversity is more significant than the difference on convergence, at least for their contribution to HV calculus, resulting in significant higher values of HV when using the new version of D-MEANDS proposed in the present work. Although the hypervolume is the most widely metric used to evaluate multiobjective algorithms (because it is non-parametric and gives this mixed perspective of diversity and convergence), in the future, it could be interesting to use other convergence metrics to have an absolute measure of how much D-MEANDS convergence is higher than D-MEANDS-MD. For example, by calculating the convergence metric discussed in (Deb and Jain, Reference Deb and Jain2002).
Figure 12. Parallel coordinates of the solutions found by D-MEANDS-MD (black dots and lines) and DDIS-MOEA/D-DE (blue) in their best runs (out of 100). DMKP instance with 4 objectives, 100 items and EC=20. The reference W0 used for HV calculus is also represented in red
Figure 13. Parallel coordinates of the solutions found by (a)(c)(e) D-MEANDS-MD and (b)(d)(f) D-MEANDS in their best runs (out of 100). DMKP instance with 100 items and EC=20. The graphs (a) (b) refer to the instance of 4 objectives, (c) (d) of 6 objectives and (e) (f) of 8 objectives
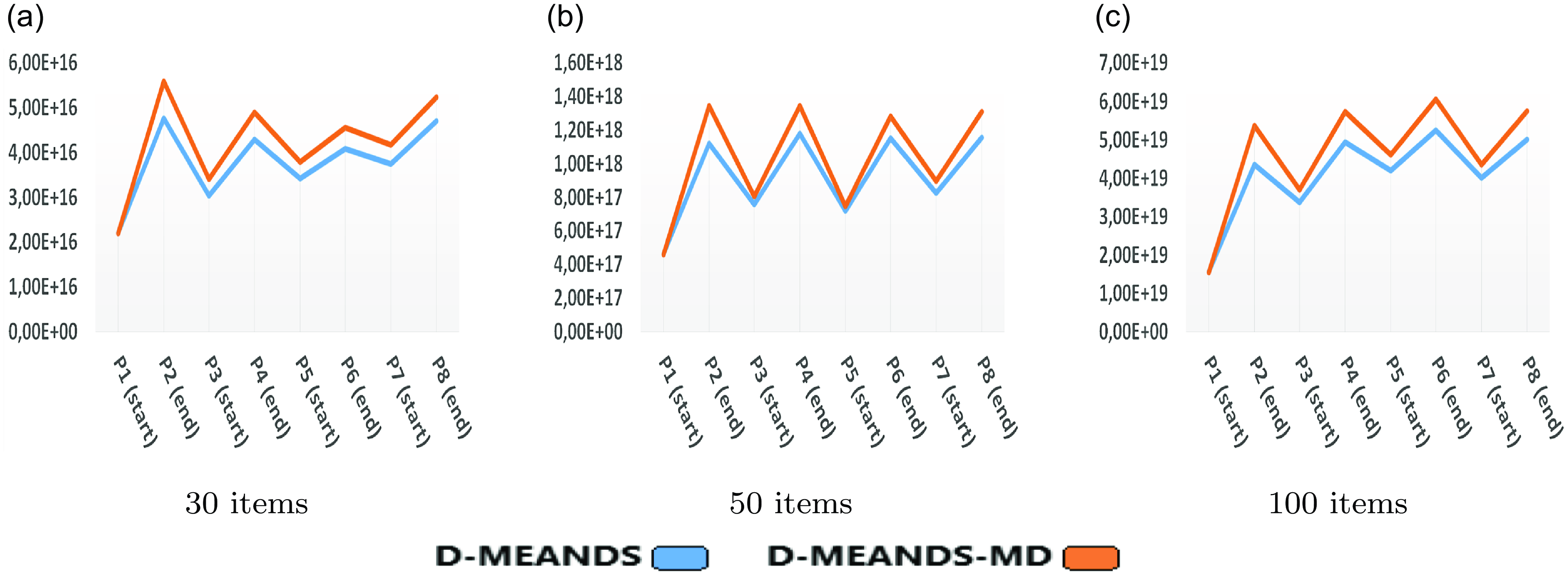
Figure 14. Average of the HVs of the start and end of each environment of 100 executions of D-MEANDs and D-MEANDS-MD in the instance of 6 objectives 30, 50 and 100 items with EC=20
5.5. Deeping the hypervolume analysis
Sections 5.2 and 5.3 show the superiority of D-MEANDS-MD over the other algorithms regarding the hypervolume metric when submitted to the same number of fitness evaluations. In this section we will continue to analyze the hypervolume but using other information to deeper evaluate these numerical results. Figures 12 and 13 show parallel coordinates graphs, which are commonly used to visualize set of solutions in multiobjective problems with many objectives (more than 3). Figure 12 shows two sets of final solutions: the black lines and points represent the final Pareto approximation found by D-MEANDS-MD in the best run in respect to HV, and the light blue lines and points represent the final set found by the best run of DDIS-MOEA/D-DE. They were obtained in the DMKP instance with 4 objectives, 100 items and EC=20. Besides, the graph also represents the reference solution (in red) used for HV calculus: w0=(0,0,0,0). Each line represents one evolved solution and it links the four values found in each objective. The axis X, Y, W, and Z represent the dimensions of the four objectives involved in the problem. The hypervolume calculated for the set found by D-MEANDS-MD is HV=4.4738E+7, while for the DDIS-MOEA/D-DE is HV=2.0549E+7. Corroborating that their hypervolumes are very different (D-MEANDS-MD value is much higher), it is clear to observe in the graph of Figure 12 the differences between the two Pareto approximations. It also makes clear that, despite the numerical values of the hypervolume, the set found by D-MEANDS-MD is clear better than the other.
However, when we try to visualize closer results, the analisys is not so clear, because the solutions from the two sets may mix in the graph. It was what happened when we try to compare the sets of solutions found by D-MEANDS-MD and D-MEANDS in the same instance of DMKP: 4 objectives, 100 items and EC=20. The hypervolume calculated for the set found by D-MEANDS is HV=3.9697E+7 (for D-MEANDS-MD, as pointed early, is HV=4.4738E+7). Therefore, the results are plotted in separate graphs, Figure 13(a) for D-MEANDS-MD and Figure 13(b) for D-MEANDS. Moreover, we noticed that when including w0=(0,0,0,0) in such graphs, the comparison of the final sets are more difficult to do. The inclusion of w0 causes the graphs scales to mix the solutions embarrassing the comparison. Therefore, w0 was not included in Figure 13.
Comparing the sets of solutions in Figure 13(a) and (b) it is possible to observe that in x and w dimensions, both sets appear to occupy a similar interval of objective values. However, considering the z dimension, the set found by D-MEANDS-MD (Figure 13(a)) stands out with a much higher values than the other (Figure 13(b)). On the other hand, considering the y dimension, the D-MEANDS-MD tends to occupy a little slower interval than the other, but the difference is not significant as the observed in dimension z. Therefore, the difference in dimension z was more preponderant in the HV calculus resulting in a higher value for the set of solutions found by D-MEANDS-MD. It is also important to highlight that the set found by D-MEANDS-MD presents points more distributed in the axis. This spreading of points causes the hypervolume to be higher, once HV calculus also represents the diversity of the final solutions, because this decreases the overlapping area of the hypercubes. This observation combined with the verification in the last subsection (by using CS metric) that in general D-MEANDS-MD does not dominate more solutions of D-MEANDS make us to conclude that both version of DMEANDS algorithm have similar convergence to the Pareto Front but the D-MEANDS-MD presents a better diversity which makes higher values of HV and AD metrics. This is a direct consequence of the new strategy of diversity included in D-MEANDS-MD.
Increasing the number of objectives returns a set of non-dominated solutions of high cardinality, making it difficult to visually analyze the graphs. However, the graphs with 6 and 8 (Figure 13) objectives were presented only for a better understanding of the shape of the curves in these other spaces. Overall, the two approaches are similar, making it difficult to visually determine which was superior. However, the HV metric shows that DMEANDS-MD performed better than its predecessor.
A final analysis was performed to investigate the change promoted by the insertion of the diversity strategy in D-MEANDS-MD considering the intervals between consecutive environmental changes. In Section 5.2, it is said that the modification implemented in D-MEANDS-MD causes the convergence to sets with better solutions in the evolutionary process observed from one EC to the other. A final experiment was designed to show that this MOEA is able to find populations with higher hypervolume in the interval between two ECs. Figure 14 presents three graphs comparing D-MEANDS-MD and D-MEANDS hypervolume performance relative to three DMKP instances with 6 objectives, where the number of items are 30, 50, and 100, respectively. Each algorithm was performed 100 times. Each run has a total of 100 generations and one environmental change was applied at each 25 generations, resulting in three ECs referred here as
![]() $C_{25}$
,
$C_{25}$
,
![]() $C_{50}$
, and
$C_{50}$
, and
![]() $C_{75}$
. The hypervolume for the current population was calculated in some points of the evolutionary search: (a) at the start of the run (initial population); (b) before the occurrence of each EC; (c) after the reinitialization of the population; and (d) at the end of the run (final solution). It results in eight control points where HV was calculated in each run. The graphs in Figure 14 present the average of HV calculated in each of these eight control points for each MOEA.
$C_{75}$
. The hypervolume for the current population was calculated in some points of the evolutionary search: (a) at the start of the run (initial population); (b) before the occurrence of each EC; (c) after the reinitialization of the population; and (d) at the end of the run (final solution). It results in eight control points where HV was calculated in each run. The graphs in Figure 14 present the average of HV calculated in each of these eight control points for each MOEA.
Considering the first graph (DMKP instance with 30 items), both algorithms start from similar values of HV (P1) but at the end of the first environment (P2), after 25 generations, its is possible to observe that the HV related to the D-MEANDS-MD solutions are higher (in average). After the first change (
![]() $C_{25}$
) and reinicialization (P3) in both MOEAs the HV value decays, as expected. However, in general, D-MEANDS-MD tends to generate a population with a slight higher HV at the beginning of the next environment, since it departs from a better set before the EC occurrence. For this reason D-MEANDS-MD reinitializes in point P3 generating populations with a slight higher HV value (compared to D-MEANDS value). In the other ECs the behavior is similar: in the points P4 and P6 (after 25 generations from the previous EC) the HV value achieved in D-MEANDS-MD is clearly higher than D-MEANDS. Moreover, after
$C_{25}$
) and reinicialization (P3) in both MOEAs the HV value decays, as expected. However, in general, D-MEANDS-MD tends to generate a population with a slight higher HV at the beginning of the next environment, since it departs from a better set before the EC occurrence. For this reason D-MEANDS-MD reinitializes in point P3 generating populations with a slight higher HV value (compared to D-MEANDS value). In the other ECs the behavior is similar: in the points P4 and P6 (after 25 generations from the previous EC) the HV value achieved in D-MEANDS-MD is clearly higher than D-MEANDS. Moreover, after
![]() $C_{50}$
and
$C_{50}$
and
![]() $C_{75}$
changes in points P5 and P7, D-MEANDS-MD departs from sets of solutions with higher HV than D-MEANDS population. As a consequence, at the end of the run (P8), D-MEANDS-MD population in average has HV values higher than D-MEANDS. Similar observations can be done for the other two graphs in Figure 14 (50 and 100 items). Since in all intervals of evolution between consecutive ECs, D-MEANDS-MD found solution sets with higher HV than those found by D-MEANDS, we can point that D-MEANDS-MD strategy exhibits a better convergence to fronts with higher HD at each environment.
$C_{75}$
changes in points P5 and P7, D-MEANDS-MD departs from sets of solutions with higher HV than D-MEANDS population. As a consequence, at the end of the run (P8), D-MEANDS-MD population in average has HV values higher than D-MEANDS. Similar observations can be done for the other two graphs in Figure 14 (50 and 100 items). Since in all intervals of evolution between consecutive ECs, D-MEANDS-MD found solution sets with higher HV than those found by D-MEANDS, we can point that D-MEANDS-MD strategy exhibits a better convergence to fronts with higher HD at each environment.
6. Conclusions
The problem investigated in this work is the DMKP (Farina et al., Reference Farina, Deb and Amato2004), which is a dynamic and discrete MOP. We deepened the investigation started in (Lafetá and Oliveira, Reference Lafetá and Oliveira2020a; Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) observing the behavior of the
![]() $DNSGA-II^*$
(Deb and Karthik, Reference Deb and Karthik2007; Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), MS-MOEA (Wang and Li, Reference Wang and Li2010) and D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) algorithms in more complex instances than they were submitted to in the previous works. Two non-parametric metrics used to evaluate DMOPs were used for the performance evaluation: Hypervolume (HV) and Density (AD). The processing time of each algorithm was also evaluated. Formulations with 4, 6, and 8 objectives were applied to instances of DMKP with 30, 50, and 100 items in the comparative analysis. Experiments were carried out by applying 10, 15, and 20 environment changes (ECs) along the evolutionary search, were the ECs were uniformly distributed over the generations.
$DNSGA-II^*$
(Deb and Karthik, Reference Deb and Karthik2007; Lafetá and Oliveira, Reference Lafetá and Oliveira2020a), MS-MOEA (Wang and Li, Reference Wang and Li2010) and D-MEANDS (Lafetá and Oliveira, Reference Lafetá and Oliveira2020b) algorithms in more complex instances than they were submitted to in the previous works. Two non-parametric metrics used to evaluate DMOPs were used for the performance evaluation: Hypervolume (HV) and Density (AD). The processing time of each algorithm was also evaluated. Formulations with 4, 6, and 8 objectives were applied to instances of DMKP with 30, 50, and 100 items in the comparative analysis. Experiments were carried out by applying 10, 15, and 20 environment changes (ECs) along the evolutionary search, were the ECs were uniformly distributed over the generations.
Analyzing the metrics HV and AD, D-MEANDS outperforms other algorithms in most instances, specially when using instances of 8 objectives. However, the increase in changing environments (EC) highlights that the D-MEANDS performance decays in relation to the others algorithms. It is worth to note that our experiments show that by increasing the complexity of the instances makes D-MEANDS processing time to relatively increase more than the others. This cost increase is due to the D-MEANDS characteristic of not having a population limit in all the subsets of nondominated solutions. In instances of 4 objectives, D-MEANDS is the faster option, close to
![]() $DNSGA-II^*$
time processing. However, with the increase in the number of objectives,
$DNSGA-II^*$
time processing. However, with the increase in the number of objectives,
![]() $DNSGA-II^*$
proves to be much faster than the other algorithms.
$DNSGA-II^*$
proves to be much faster than the other algorithms.
A proposal for a new algorithm was made in this work. This uses a simple mechanism to insert diversity into the main population of the MOEA. The use of such mechanism was evaluated in D-MEANDS and
![]() $DNSGA-II^*$
, proposing the algorithms D-MEANDS-MD and
$DNSGA-II^*$
, proposing the algorithms D-MEANDS-MD and
![]() $DNSGA-II^+$
. However, after a new series of experiments comparing the behavior of the new propositions for
$DNSGA-II^+$
. However, after a new series of experiments comparing the behavior of the new propositions for
![]() $DNSGA-II^*$
and D-MEANDS and their original versions, it was clear that this mechanism was very effective for D-MEANDS-MD, while it does not improve
$DNSGA-II^*$
and D-MEANDS and their original versions, it was clear that this mechanism was very effective for D-MEANDS-MD, while it does not improve
![]() $DNSGA-II^+$
in respect to
$DNSGA-II^+$
in respect to
![]() $DNSGA-II^*$
. A recent MOEA was also included in this comparative analysis: the DDIS-MOEA/D-DE (Liu et al., Reference Liu, Peng, Liu and Liu2020), which uses differential evolution as the underlying evolutionary search strategy. The proposal D-MEANDS-MD surpassed all the other algorithms in all the 27 instances of DMKP when the performance multiobjective metrics HV and AD are taken in account. However, its processing time is similar to D-MEANDS and it takes the longer execution time, except for the instances with 4 objectives.
$DNSGA-II^*$
. A recent MOEA was also included in this comparative analysis: the DDIS-MOEA/D-DE (Liu et al., Reference Liu, Peng, Liu and Liu2020), which uses differential evolution as the underlying evolutionary search strategy. The proposal D-MEANDS-MD surpassed all the other algorithms in all the 27 instances of DMKP when the performance multiobjective metrics HV and AD are taken in account. However, its processing time is similar to D-MEANDS and it takes the longer execution time, except for the instances with 4 objectives.
Based on the experiments performed, we could conclude that D-MEANDS-MD is a very promising MOEA for dynamic and many-objective optimization problems as the DMKP. However, it is clear that the time processing is a bottleneck to employ this algorithm if a high number of objectives, - starting from 8 - is used. This limitation is related to the basic structure of MEANDS (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016), the precursor method of D-MEANDS-MD, which was proposed for static MaOPs. In both algorithms, the number of sub-populations manipulated in a single run increases exponentially with the increment of the number of objectives, causing this severe extra demand in processing time.
Therefore, we intend to investigate how to modify D-MEANDS and D-MEANDS-MD to surpass this limitation. A similar effort was made to turn the precursor MEANDS to be viable for static problems defined for continuous spaces proposing the algorithm MEANDS2 (Lafeta and Oliveira, Reference Lafeta and Oliveira2019). However, the strategies used for static problems did not shown efficient for dynamic problems and we discarded the use of MEANDS2 as the subjacent framework for discrete DMOPs. We intend to investigate other strategies to limit the sub-populations grouth to enable the application of D-MEANDS-MD in dynamic problems with a high number of objectives (
![]() $ \gt $
8). Moreover, we plan to apply D-MEANDS-MD to other problems, such as the dynamic multicast routing, where MEANDS was previously applied to its static version (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016). In addition, we intend to expand our set of non-parametric metrics, with focus on evaluating both convergence and diversity. Another future investigation is to investigate how to adapt D-MEANDS for continuous and dynamic MaOPs.
$ \gt $
8). Moreover, we plan to apply D-MEANDS-MD to other problems, such as the dynamic multicast routing, where MEANDS was previously applied to its static version (Lafeta et al., Reference Lafeta, Bueno, Brasil and Oliveira2016). In addition, we intend to expand our set of non-parametric metrics, with focus on evaluating both convergence and diversity. Another future investigation is to investigate how to adapt D-MEANDS for continuous and dynamic MaOPs.
Regarding the comparative analysis of MOEAs performance in dynamical problems, it is important to ensure that all algorithms were submitted to the same number of environmental changes in each execution. Our test environment was configured to apply a new change at each fixed interval of generations. Therefore, all the investigated MOEAs have to use the same total of generations to face the same changes in each run. Besides, at each change occurrence, the metrics (HV, IGD, etc) are calculated, being that the average of these metrics are computed at the end of the run and the mean values of the metrics are used to compare MOEAs performance. Therefore, this stopping condition allows us to control the amount of environment changes in the executions independently of the MOEA applied. Furthermore, the stopping condition based on the number of generations together with the control of the number of crossovers per generation is widely used in the evolutionary computing literature because it allows one to make a fair comparative evaluation of two or more algorithms assuring that they compute the same number of fitness evaluations in a run, that is, the same number of points of the search space is explored in a single run. Moreover, it makes this comparison more independent of the personal implementation of the algorithm, which can turn it lower or faster depending on the programmer’s coding. However, we agree that the stopping condition based on the total time would have a more practical perspective for a real-world problem. Therefore, as a future work, we are planning to construct a new test environment not only stopping the execution by a limiting time but also applying the changes by each time interval. In this way, we will also have a controlled environment to compare different MOEAs where their processing time efficiency will also affect their convergence to a good Pareto. In such case we will use the number of explored solutions to evaluate the efficacy of each approach.
Acknowledgment
The authors thank FAPEMIG, CAPES, and CNPq.































