Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dong, Wei
2004.
Symmetry for boundary blow up solutions of elliptic equations in a half-space.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 58,
Issue. 1-2,
p.
159.
Farina, Alberto
Montoro, Luigi
and
Sciunzi, Berardino
2012.
Monotonicity and one-dimensional symmetry for solutions of −Δ p u = f(u) in half-spaces.
Calculus of Variations and Partial Differential Equations,
Vol. 43,
Issue. 1-2,
p.
123.
Farina, Alberto
Montoro, Luigi
and
Sciunzi, Berardino
2013.
Monotonicity of solutions of quasilinear degenerate elliptic equation in half-spaces.
Mathematische Annalen,
Vol. 357,
Issue. 3,
p.
855.
Farina, Alberto
2014.
James Serrin. Selected Papers.
p.
363.
Farina, Alberto
Montoro, Luigi
Riey, Giuseppe
and
Sciunzi, Berardino
2015.
Monotonicity of solutions to quasilinear problems with a first-order term in half-spaces.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 32,
Issue. 1,
p.
1.
Sciunzi, Berardino
2015.
Monotonicity results in half-spaces for thep-Laplacian.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 145,
Issue. 3,
p.
597.
Efendiev, Messoud
2018.
Symmetrization and Stabilization of Solutions of Nonlinear Elliptic Equations.
Vol. 36,
Issue. ,
p.
225.
Covei, Dragos-Patru
2019.
Symmetric solutions for an elliptic partial differential equation that arises in stochastic production planning with production constraints.
Applied Mathematics and Computation,
Vol. 350,
Issue. ,
p.
190.
Montoro, Luigi
2021.
Harnack Inequalities and Nonlinear Operators.
Vol. 46,
Issue. ,
p.
159.
Chen, Yujuan
Wei, Lei
and
Zhang, Yimin
2022.
The Asymptotic Behavior and Symmetry of Positive Solutions to p-Laplacian Equations in a Half-Space.
Acta Mathematica Scientia,
Vol. 42,
Issue. 5,
p.
2149.
Esposito, Francesco
Farina, Alberto
Montoro, Luigi
and
Sciunzi, Berardino
2022.
Monotonicity of positive solutions to quasilinear elliptic equations in half-spaces with a changing-sign nonlinearity.
Calculus of Variations and Partial Differential Equations,
Vol. 61,
Issue. 4,
Ibrahim, H.
and
Younes, R.
2023.
Existence of quasilinear elliptic equations with prescribed limiting behavior.
Asymptotic Analysis,
Vol. 134,
Issue. 3-4,
p.
553.
Le, Phuong
2023.
Uniqueness of bounded solutions to p-Laplace problems in strips.
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G4,
p.
795.
Le, Phuong
2024.
Sliding method and one-dimensional symmetry for p-Laplace equations.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 4,
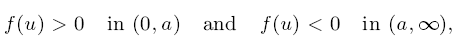 but not necessarily Lipschitz continuous, we study the quasi-linear equation
but not necessarily Lipschitz continuous, we study the quasi-linear equation
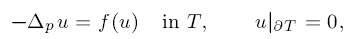 where T = {x = (x1, x2, …, xN) ∈ RN: x1 > 0} with N ≥ 2. By using a new approach based on the weak maximum principle, we show that any positive solution on T must be a function of x1 only. Under our assumptions, the strong maximum principle does not hold in general and the solution may develop a flat core; our symmetry result allows an easy and precise determination of the flat core.
where T = {x = (x1, x2, …, xN) ∈ RN: x1 > 0} with N ≥ 2. By using a new approach based on the weak maximum principle, we show that any positive solution on T must be a function of x1 only. Under our assumptions, the strong maximum principle does not hold in general and the solution may develop a flat core; our symmetry result allows an easy and precise determination of the flat core.

