Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T18:18:49.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial regularity of strong local minimizers of quasiconvex integrals with (p, q)-growth

Published online by Cambridge University Press:  26 May 2009

Sabine Schemm  and
Thomas Schmidt
Sabine Schemm
Affiliation:
Mathematisches Institut, Friedrich-Alexander-Universität Erlangen-Nürnberg, Bismarckstrasse 1 1/2, 91054 Erlangen, Germany (schemm@mi.uni-erlangen.de)
Thomas Schmidt
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität Düsseldorf, Universitätsstrasse 1, 40225 Düsseldorf, Germany (schmidt.th@uni-duesseldorf.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider strictly quasiconvex integrals

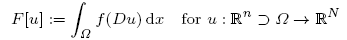
in the multi-dimensional calculus of variations. For the C2-integrand f : ℝNn → ℝ we impose (p, q)-growth conditions

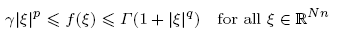
with γ, Γ > 0 and 1 < p ≤ q < min {p + 1/n, p(2n − 1)/(2n − 2)}. Under these assumptions we prove partial C1, αloc-regularity for strong local minimizers of F and the associated relaxed functional .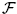

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 139 , Issue 3 , June 2009 , pp. 595 - 621
Copyright
Copyright © Royal Society of Edinburgh 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)