Moment bounds for the solutions of the Smoluchowski equation with coagulation and fragmentation
Published online by Cambridge University Press: 01 October 2010
Abstract
We prove various 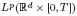 bounds on moments
bounds on moments
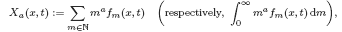
where fm is a solution of the discrete (respectively, continuous) Smoluchowski coagulation–fragmentation equations with diffusion. In a previous paper we proved similar results for all weak solutions to the discrete Smoluchowski equation provided that there is no fragmentation and certain moments are bounded in suitable Lq-spaces initially. We prove the corresponding results in the case of the continuous Smoluchowski equation. When there is also fragmentation, we need to assume that the solution f is regular in the sense that f can be approximated by solutions to the Smoluchowski equation for which the coagulation and fragmentation coefficients are 0 when the cluster sizes are large. We also need suitable assumptions on the coagulation rates to avoid gelation. On the fragmentation rate β we assume that supn supm≤l β(m, n)/n < ∞ for every positive l, and that there exist constants a0 ≥ 0 and c0 such that β(n,m) ≤ c0(n + m)a0a0.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 140 , Issue 5 , October 2010 , pp. 1041 - 1059
- Copyright
- Copyright © Royal Society of Edinburgh 2010
- 12
- Cited by


