Convex-transitive characterizations of Hilbert spaces
Published online by Cambridge University Press: 26 May 2009
Abstract
We investigate real convex-transitive Banach spaces X, which admit a one-dimensional bicontractive projection P on X. Various mild conditions regarding the weak topology and the geometry of the norm are provided, which guarantee that such an X is in fact isometrically a Hilbert space. For example, if u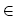 SX is a big point such that there is a bicontractive linear projection P : X → [u] and X* is weak*-locally uniformly rotund, then X is a Hilbert space. The results obtained here are motivated by the well-known Banach—Mazur rotation problem, as well as a question posed by B. Randrianantoanina in 2002 about convex-transitive spaces.
SX is a big point such that there is a bicontractive linear projection P : X → [u] and X* is weak*-locally uniformly rotund, then X is a Hilbert space. The results obtained here are motivated by the well-known Banach—Mazur rotation problem, as well as a question posed by B. Randrianantoanina in 2002 about convex-transitive spaces.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 139 , Issue 3 , June 2009 , pp. 633 - 659
- Copyright
- Copyright © Royal Society of Edinburgh 2009
- 1
- Cited by


