Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T11:22:24.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness of bounded trajectories of dynamical systems in infinite dimensional spaces†

Published online by Cambridge University Press:  14 November 2011

G. F. Webb
G. F. Webb
Affiliation:
Mathematics Department, Vanderbilt University, Nashville, Tennessee 37235, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

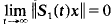The following theorem is proved: Let S(t), t≧0 be a dynamical system in an infinite dimensional Banach space X such that S(t) = S1(t)+S2(t) for t≧0, where (1) uniformly in bounded sets of x in X, and (2) S2(t) is compact for t sufficiently large. Then, if the orbit {S(t)x: t ≧0} of x ∈ X is bounded in X, it is precompact in X. Applications are made to an age dependent population model, a non-linear functional differential equation on an infinite interval, and a non-linear Volterra integrodifferential equation.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 1-2 , 1979 , pp. 19 - 33
Copyright
Copyright © Royal Society of Edinburgh 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ball, J.. Saddle point analysis for an ordinary differential equation in a Banach space and an application to dynamic buckling of a beam. In Nonlinear elasticity ed. Dickey, R. W., pp. 93–160. (New York: Academic Press, 1973).Google Scholar
2Ball, J.. Initial-boundary value problems for an extensible beam. J. Math. Anal. Appl. 42 (1973), 61–90.CrossRefGoogle Scholar
3Ball, J.On the asymptotic behavior of generalized processes with applications to nonlinear evolution equations. J. Math. Anal. Appl. 27 (1978), 224–265.Google Scholar
4Dafermos, C. and Slemrod, M.. Asymptotic behavior of nonlinear contraction semigroups. J. Functional Analysis 13 (1973), 97–106.CrossRefGoogle Scholar
5Darbo, G.. Punti uniti in trasformazioni a condominio non compatto. Rend. Sem. Mat. Univ. Padova 24 (1955), 84–92.Google Scholar
6Dunford, N. and Schwartz, J.. Linear operators, Pt I (New York: Interscience, 1957).Google Scholar
7Gurtin, M. and MacCamy, R.. Non-linear age-dependent population dynamics. Arch. Rational Mech. Anal. 54 (1974), 281–300.CrossRefGoogle Scholar
8Hale, J.. Dynamical systems and stability. J. Math. Anal. Appl. 26 (1969), 39–59.CrossRefGoogle Scholar
9Hale, J.. Functional differential equations. Appl. Math. Sci., Vol. 3 (Berlin: Springer, 1971).Google Scholar
10Hale, J.. Functional differential equations with infinite delays. J. Math. Anal. Appl. 48 (1974), 276–283.CrossRefGoogle Scholar
11Henry, D.. Geometric theory of similinear parabolic equations (to appear).Google Scholar
12Hoppensteadt, F.. Mathematical theories of populations: demographics, genetics, and epidemics.SIAM Regional Conference Series in Applied Mathematics, Philadelphia, 1975.CrossRefGoogle Scholar
13Kuratowskii, C.. Topology, I (New York: Academic Press, 1966).Google Scholar
14Pazy, A.. A class of semi-linear equations of evolution. Israel J. Math. 20 (1975), 23–36.Google Scholar
15Travis, C. and Webb, G.. Existence and stability for partial functional differential equations. Trans. Amer. Math. Soc. 200 (1974), 395–418.CrossRefGoogle Scholar
16Walker, J.. An introduction to dynamical systems: theory and applications. Lecture Notes, Technological Institute, Northwestern University, Evanston, Illinois, 1978.Google Scholar
17Walker, J. and Infante, E.. Some results on the precompactness of orbits of dynamical systems. J. Math. Anal. Appl. 51 (1975), 56–66.Google Scholar
18Webb, G.. Autonomous nonlinear functional differential equations and nonlinear semigroups. J. Math. Anal. Appl. 46 (1974), 1–12.Google Scholar
19Webb, G.. Asymptotic stability for abstract nonlinear functional differential equations. Proc. Amer. Math. Soc. 54 (1976), 225–230.CrossRefGoogle Scholar
20Webb, G.. Functional differential equations and nonlinear semigroups in L p-spaces. J. Differential Equations 20 (1976), 71–89.CrossRefGoogle Scholar
21Webb, G.. Volterra integral equations as functional differential equations on infinite intervals. Hiroshima Math. J. 7 (1977), 61–70.CrossRefGoogle Scholar
22Webb, G.. A bifurcation problem for a nonlinear hyperbolic partial differential equation. SIAM J. Math. Anal, (to appear).Google Scholar
23Webb, G.. Existence and asymptotic behavior for a strongly damped nonlinear wave equation (to appear).Google Scholar
24Yosida, K.. Functional analysis (New York: Springer, 1968).CrossRefGoogle Scholar
25Brewer, D. W.. A nonlinear semigroup for a functional differential equation. Trans. Amer. Math. Soc. 236 (1978), 173–191.Google Scholar
26Brewer, D. W.. A nonlinear contraction semigroup for a functional differentialequation, to appear in the Proc. Helsinki Symp. Integral Equations,1978.CrossRefGoogle Scholar