The Golod-Shafarevich inequality for Hilbert series of quadratic algebras and the Anick conjecture
Published online by Cambridge University Press: 03 June 2011
Abstract
We study the question of whether the famous Golod-Shafarevich estimate, which gives a lower bound for the Hilbert series of a (non-commutative) algebra, is attained. This question was considered by Anick in his 1983 paper, ‘Generic algebras and CW-complexes’ (Princeton University Press), where he proved that the estimate is attained for the number of quadratic relations d ≤ ¼n2 and d ≥ ½n2, and conjectured that it is the case for any number of quadratic relations. The particular point where the number of relations is equal to ½n(n – 1) was addressed by Vershik. He conjectured that a generic algebra with this number of relations is finite dimensional.
We prove that over any infinite field, the Anick conjecture holds for d ≥ 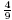 (n2 + n) and an arbitrary number of generators n, and confirm the Vershik conjecture over any field of characteristic 0. We give also a series of related asymptotic results.
(n2 + n) and an arbitrary number of generators n, and confirm the Vershik conjecture over any field of characteristic 0. We give also a series of related asymptotic results.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 141 , Issue 3 , June 2011 , pp. 609 - 629
- Copyright
- Copyright © Royal Society of Edinburgh 2011
- 4
- Cited by


