Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-22T05:23:09.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Two infinite integrals

Published online by Cambridge University Press:  20 January 2009

G. N. Watson
G. N. Watson
Affiliation:
The University, Birmingham
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The infinite integrals

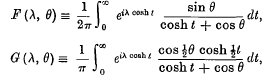
in which λ is positive and – π < θ < π were encountered by Kottler in a problem in the theory of diffraction. They have more recently been studied by Copson and Ferrar, who obtained the remarkably simple Fourier series

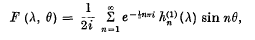
in which 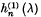denotes a “cut Bessel function” of the third kind; this expansion is valid when 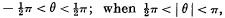the term 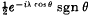has to be added to the expansion on the right.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 5 , Issue 4 , September 1938 , pp. 174 - 181
Copyright
Copyright © Edinburgh Mathematical Society 1938

References

page 174 note 1 Kottler, F., Ann. der Physik, 71 (1923), 457–508.CrossRefGoogle Scholar

page 174 note 2 Copson, E. T. and Ferrar, W. L., these Proceedings (2), 5 (1938), 159–168.Google Scholar

page 174 note 3 (Added in proof, 15th August, 1938.) I take this opportunity of making two remarks: (i) Prof. Copson has pointed out to me that, in the actual physical problem discussed by Kottler, no more is required than the approximate behaviour of F(λ, θ) and of G(λ, θ) when λ is small and also when λ is large; I must, therefore, admit that, for the purposes of this problem, the Copson-Ferrar formulae are completely adequate and my own formulae contain superfluous and irrelevant information, (ii) Mr Ferrar has informed me that Dr Artur Erdélyi has written to him to point out that it is easy to derive a finite integral representing F(λ, θ) by means of Kottler's differential equation, and hence to obtain the expansion of F(λ, θ) for small values of λ.

page 176 note 1 See my Theory of Bessel functions (Cambridge, 1922), 170.Google Scholar

page 176 note 2 See my Theory of Bessel functions, 191.Google Scholar

page 177 note 1 The labour of computing fn (λ) by means of this expansion is comparable with the labour of computing Bessel functions of the second kind.

page 180 note 1 The recurrence formula for gn (λ) is