Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T09:29:05.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Unitary Representations of Some Linear Groups

Published online by Cambridge University Press:  22 January 2016

Seizô Itô
Seizô Itô*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently I. Gelfand and M. Neumark [2] have determined the types of irreducible unitary representations of the group G1 of linear transformations of the straight line. The analogous result is obtained for the group G2 of transformations z → az + b in the complex-number plane 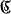, where a and b run over all complex numbers with the exception of a = 0, which may be considered as the group of all sense-preserving similar transformations in the two-dimensional euclidean space E2.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 4 , June 1952 , pp. 1 - 13
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1952

References

Literature

[1] Doob, J. L.: Stochastic processes with an integral-valued parameter, Trans. Amer. Math, Soc. 44 (1938).Google Scholar
[2] Gelfand, I. and Neumark, M.: Unitary representations of the group of linear transformations of the straight line, C. R. (Doklady) Acad. Sci. URSS. 55 (1947) pp. 567–570.Google Scholar
[3] Godement, R.: Les fonctions de type positif et la théorie des groupes, Trans. Amer. Math. Soc. 63, No. 1 (1948) pp. 1–84.Google Scholar
[4] Slutsky, E.: Sur les fonctions aléatoires presque périodiques et sur la décomposition des fonctions aléatoires stationaires en composantes, Act. Sci. Ind. 738 (1938).Google Scholar
[5] Stone, M. H.: Linear transformations in Hilbert spaces and their applications to analysis, New York (1932).Google Scholar