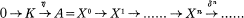Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mahowald, Mark
and
Tangora, Martin
1968.
An infinite subalgebra of 𝐸𝑥𝑡_{𝐴}(𝑍₂,𝑍₂).
Transactions of the American Mathematical Society,
Vol. 132,
Issue. 1,
p.
263.
Kono, Akira
and
Mimura, Mamoru
1975.
Cohomology mod 2 of the classifying space of the compact connected lie group of type E6.
Journal of Pure and Applied Algebra,
Vol. 6,
Issue. 1,
p.
61.
Kono, Akira
Mimura, Mamoru
and
Shimada, Nobuo
1976.
On the cohomology mod 2 of the classifying space of the 1-connected exceptional Lie group E7.
Journal of Pure and Applied Algebra,
Vol. 8,
Issue. 3,
p.
267.
Davis, Donald M.
and
Mahowald, Mark
1978.
The immersion conjecture for 𝑅𝑃^{8𝑙+7} is false.
Transactions of the American Mathematical Society,
Vol. 236,
Issue. 0,
p.
361.
1986.
Vol. 121,
Issue. ,
p.
395.
Ando, Yutaka
1989.
Cohomology of a Hopf algebra over $Z_2$.
Kodai Mathematical Journal,
Vol. 12,
Issue. 3,
Monks, Kenneth G.
1992.
Nilpotence and torsion in the cohomology of the Steenrod algebra.
Transactions of the American Mathematical Society,
Vol. 333,
Issue. 2,
p.
903.
Tezuka, Michishige
1994.
Cohomology of unipotent algebraic and finite groups and the Steenrod algebra.
Mathematische Zeitschrift,
Vol. 216,
Issue. 1,
p.
45.
Bruner, Robert
and
Rognes, John
2022.
The Adams spectral sequence for the image-of-𝐽 spectrum.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 8,
p.
5803.
Quigley, J D
2022.
tmf–based Mahowald invariants.
Algebraic & Geometric Topology,
Vol. 22,
Issue. 4,
p.
1789.
Yu, Xiaolan
and
Yang, Jingting
2023.
Cohomology of Graded Twisting of Hopf Algebras.
Mathematics,
Vol. 11,
Issue. 12,
p.
2759.
Basile, Ivano
Debray, Arun
Delgado, Matilda
and
Montero, Miguel
2024.
Global anomalies & bordism of non-supersymmetric strings.
Journal of High Energy Physics,
Vol. 2024,
Issue. 2,
Debray, Arun
2024.
Higher Structures in Topology, Geometry, and Physics.
Vol. 802,
Issue. ,
p.
227.
Behrens, M.
Bhattacharya, P.
and
Culver, D.
2025.
The structure of the $$v_2$$-local algebraic $$\text {tmf}$$ resolution.
Mathematische Zeitschrift,
Vol. 310,
Issue. 1,