Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T08:15:52.025Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of H. F. Blichfeldt

Published online by Cambridge University Press:  22 January 2016

Noboru Itô
Noboru Itô*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1903 H. F. Blichfeldt proved the following brilliant theorem : Let G be a matrix group of order g and of degree n. Let p be a prime divisor of g such that 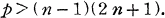Then G contains the abelian normal p-Sylow subgroup. In 1941 applying his modular theory of the group representation, R. Brauer improved this theorem in the case in which p divides g to the first power only. Further in 1943 H. F. Tuan improved this result of R. Brauer one step more.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 5 , February 1953 , pp. 75 - 77
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1953

References

1 On the order of linear homogeneous groups, Transactions Am. Math. Soc, vol. 4 (1903), 387-397.

2 On groups whose order contains a prime number to the first power II, American Journal of Mathematics, vol. 54 (1942), 421-440.

3 On groups whose orders contain a prime number to the first power, Annals of Mathematics, vol. 45 (1944), 110-140.

4 A note on soluble groups, Journal London Math. Soc, 3 (1928), 98-105.

5 Itô, N., On the degrees of irreducible representations of a finite group, These Journal, vol. 3 (1951), 5–6 Google Scholar.

6 Zerlegung der Charaktere einer Gruppe in die ihres Normalteilers, Jap. J. of Math., 12 (1935), 95-98. cf. I. Schur, Arithmetische Untersuchungen über endliche Gruppen linearer Substitutionen, Sitzb. Berlin, (1906), 164-184.

7 Itô, N., On the characters of soluble groups, These Journal, vol. 3 (1951), 31–48 Google Scholar.

8 Čunihin, S., O II-svoĭstvah konečnyh grupp, Math. sb., 25 (67) (1949), 321–346 Google Scholar.