Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-18T23:30:44.063Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSTRUCTING NONPROXY SMALL TEST MODULES FOR THE COMPLETE INTERSECTION PROPERTY

Part of: Commutative algebra: Homological methods Local rings and semilocal rings

Published online by Cambridge University Press:  21 June 2021

BENJAMIN BRIGGS Open the ORCID record for BENJAMIN BRIGGS [Opens in a new window] ,
ELOÍSA GRIFO Open the ORCID record for ELOÍSA GRIFO [Opens in a new window]  and
JOSH POLLITZ Open the ORCID record for JOSH POLLITZ [Opens in a new window]
BENJAMIN BRIGGS
Affiliation:
Department of Mathematics University of UtahSalt Lake City, UT 84112USAbriggs@math.utah.edu
ELOÍSA GRIFO
Affiliation:
Department of Mathematics University of Nebraska—LincolnNE 68588USAgrifo@unl.edu
JOSH POLLITZ
Affiliation:
Department of Mathematics University of UtahSalt Lake City, UT 84112USApollitz@math.utah.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A local ring R is regular if and only if every finitely generated R-module has finite projective dimension. Moreover, the residue field k is a test module: R is regular if and only if k has finite projective dimension. This characterization can be extended to the bounded derived category 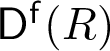$\mathsf {D}^{\mathsf f}(R)$ , which contains only small objects if and only if R is regular. 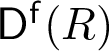Recent results of Pollitz, completing work initiated by Dwyer–Greenlees–Iyengar, yield an analogous characterization for complete intersections: R is a complete intersection if and only if every object in $\mathsf {D}^{\mathsf f}(R)$ is proxy small. In this paper, we study a return to the world of R-modules, and search for finitely generated R-modules that are not proxy small whenever R is not a complete intersection. We give an algorithm to construct such modules in certain settings, including over equipresented rings and Stanley–Reisner rings.

MSC classification

Primary: 13D09: Derived categories
Secondary: 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.)
Type
Article
Information
Nagoya Mathematical Journal , Volume 246 , June 2022 , pp. 412 - 429
Check for updates
Copyright
© (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported by the National Science Foundation grant DMS-2001445. The third author was supported by the National Science Foundation grant DMS-2002173 and the National Science Foundation Research Training Group grant DMS-1840190.

References

Auslander, M. and Buchsbaum, D. A., Homological dimension in local rings , Trans. Amer. Math. Soc. 85 (1957), 390–405.CrossRefGoogle Scholar
Avramov, L. L., Modules of finite virtual projective dimension , Invent. Math. 96 (1989), 71–101.CrossRefGoogle Scholar
Avramov, L. L., “Infinite free resolutions” in Six Lectures on Commutative Algebra, Mod. Birkhäuser Class., Birkhäuser, Basel, Progress in Mathematics 166(2010), 1–118.Google Scholar
Avramov, L. L. and Buchweitz, R.-O., Homological algebra modulo a regular sequence with special attention to codimension two , J. Algebra 230 (2000), 24–67.CrossRefGoogle Scholar
Avramov, L. L. and Buchweitz, R.-O., Support varieties and cohomology over complete intersections , Invent. Math. 142 (2000), 285–318.10.1007/s002220000090CrossRefGoogle Scholar
Avramov, L. L., Buchweitz, R.-O., Iyengar, S. B., and Miller, C., Homology of perfect complexes , Adv. Math. 223 (2010), 1731–1781.CrossRefGoogle Scholar
Avramov, L. L., Foxby, H.-B., and Herzog, B., Structure of local homomorphisms , J. Algebra 164 (1994), 124–145.10.1006/jabr.1994.1057CrossRefGoogle Scholar
Avramov, L. L., Gasharov, V. N., and Peeva, I. V., Complete intersection dimension , Inst. Hautes Études Sci. Publ. Math. 86 (1998), 67–114.CrossRefGoogle Scholar
Avramov, L. L. and Herzog, J., Jacobian criteria for complete intersections. The graded case , Invent. Math. 117 (1994), 75–88.CrossRefGoogle Scholar
Avramov, L. L. and Iyengar, S. B., “Restricting homology to hypersurfaces” in Geometric and Topological Aspects of the Representation Theory of Finite Groups, Springer Proc. Math. Stat. 242, Springer, Cham, 2018, 1–23.Google Scholar
Avramov, L. L., Iyengar, S. B., and Lipman, J., Reflexivity and rigidity for complexes. I. Commutative rings , Algebra Number Theory 4 (2010), 47–86.CrossRefGoogle Scholar
Avramov, L. L. and Sun, L.-C., Cohomology operators defined by a deformation , J. Algebra 204 (1998), 684–710.CrossRefGoogle Scholar
Bass, H. and Pavaman Murthy, M., Grothendieck groups and Picard groups of abelian group rings , Ann. Math. (2) 86 (1967), 16–73.CrossRefGoogle Scholar
Bergh, P. A., On complexes of finite complete intersection dimension , Homology Homotopy Appl. 11 (2009), 49–54.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Algèbre commutative. Chapitres 8 et 9 , reprint of the 1983 original. Springer, Berlin and Germany, 2006.Google Scholar
Briggs, B., Vasconcelos’ conjecture on the conormal module, preprint, 2020. arXiv:2006.04247.Google Scholar
Briggs, B. and Iyengar, S. B., Rigidity properties of the cotangent complex, preprint, 2020. arXiv:2010.13314.Google Scholar
Briggs, B., Iyengar, S. B., Letz, J. C., and Pollitz, J., Locally complete intersection maps and the proxy small property , to appear in Int. Math. Res. Not. IMRN (2021) https://doi.org/10.1093/imrn/rnab041.CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Cambridge Stud. Adv. Math. 39, Cambridge Univ. Press, Cambridge, MA, 1993.Google Scholar
Burke, J. and Walker, M. E., Matrix factorizations in higher codimension , Trans. Amer. Math. Soc. 367 (2015), no. 5, 3323–3370.CrossRefGoogle Scholar
Dwyer, W. G., Greenlees, J. P. C., and Iyengar, S. B., Duality in algebra and topology , Adv. Math. 200 (2006), 357–402.CrossRefGoogle Scholar
Dwyer, W. G., Greenlees, J. P. C., and Iyengar, S. B., Finiteness in derived categories of local rings , Comment. Math. Helv. 81 (2006), 383–432.CrossRefGoogle Scholar
Eisenbud, D., Homological algebra on a complete intersection, with an application to group representations , Trans. Amer. Math. Soc. 260 (1980), no. 1, 35–64.CrossRefGoogle Scholar
Gheibi, M., Jorgensen, D. A., and Takahashi, R., Quasi-projective dimension , to appear in Pacific J. Math. (2021).CrossRefGoogle Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry, http://www.math.uiuc.edu/Macaulay2.Google Scholar
Greenlees, J. P. C. and Stevenson, G., Morita theory and singularity categories , Adv. Math. 365 (2020), 107055.CrossRefGoogle Scholar
Gulliksen, T. H., A change of ring theorem with applications to Poincaré series and intersection multiplicity , Math. Scand. 34 (1974), 167–183.CrossRefGoogle Scholar
Gulliksen, T. H. and Levin, G., Homology of Local Rings. Queen’s Paper Pure Appl. Math. 20, Queen’s Univ., Kingston, ON, 1969.Google Scholar
Hopkins, M. J., “Global methods in homotopy theory” in Homotopy Theory (Durham, 1985), London Math. Soc. Lecture Note Ser. 117, Cambridge Univ. Press, Cambridge, MA, 1987, 73–96.Google Scholar
Jorgensen, D. A., Support sets of pairs of modules , Pacific J. Math. 207 (2002), 393–409.CrossRefGoogle Scholar
Krause, H., Derived categories, resolutions, and brown representability , Contemp. Math. 436 (2007), 101–139.CrossRefGoogle Scholar
Letz, J. C., Local to global principles for generation time over Noether algebras , to appear in Homology Homotopy Appl. 23 (2021), no. 2.CrossRefGoogle Scholar
Leuschke, G. J. and Wiegand, R., Cohen–Macaulay Representations, Math. Surveys Monogr. 181, Amer. Math. Soc., Providence, RI, 2012.CrossRefGoogle Scholar
Neeman, A., The chromatic tower for D(R) , Topology 31 (1992),519–532. With an appendix by M. Bökstedt.CrossRefGoogle Scholar
Pollitz, J., The derived category of a locally complete intersection ring , Adv. Math. 354 (2019), 106752.CrossRefGoogle Scholar
Pollitz, J., Cohomological supports over derived complete intersections and local rings , to appear in Math. Z. (2021) https://doi.org/10.1007/s00209-021-02738-2.CrossRefGoogle Scholar
Serre, J.-P., “Sur la dimension homologique des anneaux et des modules noethériens” in Proceedings of the International Symposium on Algebraic Number Theory, Tokyo & Nikko, 1955, Science Council of Japan, Tokyo, 1956, 175–189.Google Scholar
Shamir, S., Cellular approximations and the Eilenberg–Moore spectral sequence , Algebr. Geom. Topol. 9 (2009), 1309–1340.CrossRefGoogle Scholar
Tate, J., Homology of Noetherian rings and local rings , Ill. J. Math. 1 (1957), 14–27.Google Scholar
Vasconcelos, W. V., Ideals generated by R-sequences , J. Algebra 6 (1967), 309–316.CrossRefGoogle Scholar