Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, William W.L.
and
Travaglini, Giancarlo
2009.
Deterministic and probabilistic discrepancies.
Arkiv för Matematik,
Vol. 47,
Issue. 2,
p.
273.
Brandolini, Luca
Gigante, Giacomo
and
Travaglini, Giancarlo
2014.
A Panorama of Discrepancy Theory.
Vol. 2107,
Issue. ,
p.
159.
Chen, William
and
Skriganov, Maxim
2014.
A Panorama of Discrepancy Theory.
Vol. 2107,
Issue. ,
p.
3.
Travaglini, G.
and
Tupputi, M. R.
2016.
A Characterization Theorem for the $$L^{2}$$ L 2 -Discrepancy of Integer Points in Dilated Polygons.
Journal of Fourier Analysis and Applications,
Vol. 22,
Issue. 3,
p.
675.
Brandolini, L.
Gariboldi, B.
Gigante, G.
and
Monguzzi, A.
2024.
Single radius spherical cap discrepancy on compact two-point homogeneous spaces.
Mathematische Zeitschrift,
Vol. 308,
Issue. 3,
Bilyk, Dmitriy
Mastrianni, Michelle
and
Steinerberger, Stefan
2024.
Single radius spherical cap discrepancy via gegenbadly approximable numbers.
Advances in Mathematics,
Vol. 452,
Issue. ,
p.
109812.
Brandolini, Luca
Gariboldi, Bianca
and
Gigante, Giacomo
2025.
The Mathematical Heritage of Guido Weiss.
p.
101.
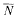 (ρ) the number N(ρ; ω) averaged over ω in the elementary cell Ω of the lattice Γ. The main result is the following lower bound for
(ρ) the number N(ρ; ω) averaged over ω in the elementary cell Ω of the lattice Γ. The main result is the following lower bound for 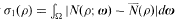 for dimensions d ≅ l(mod 4):
for dimensions d ≅ l(mod 4):