Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-18T15:19:18.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Reducing number field defining polynomials: an application to class group computations

Part of: Computational number theory Algebraic number theory: global fields

Published online by Cambridge University Press:  26 August 2016

Alexandre Gélin  and
Antoine Joux
Alexandre Gélin
Affiliation:
Sorbonne Universités, UPMC Paris 6, UMR 7606, LIP6, 75005, Paris, France email alexandre.gelin@lip6.fr
Antoine Joux
Affiliation:
Chaire de Cryptologie, Fondation UPMC, Sorbonne Universités, UPMC Paris 6, UMR 7606, LIP6, 75005, Paris, France email antoine.joux@m4x.org

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we describe how to compute smallest monic polynomials that define a given number field 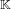$\mathbb{K}$. We make use of the one-to-one correspondence between monic defining polynomials of 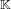$\mathbb{K}$ and algebraic integers that generate 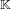$\mathbb{K}$. Thus, a smallest polynomial corresponds to a vector in the lattice of integers of 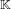$\mathbb{K}$ and this vector is short in some sense. The main idea is to consider weighted coordinates for the vectors of the lattice of integers of 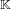$\mathbb{K}$. This allows us to find the desired polynomial by enumerating short vectors in these weighted lattices. In the context of the subexponential algorithm of Biasse and Fieker for computing class groups, this algorithm can be used as a precomputation step that speeds up the rest of the computation. It also widens the applicability of their faster conditional method, which requires a defining polynomial of small height, to a much larger set of number field descriptions.

MSC classification

Primary: 11Y40: Algebraic number theory computations
Secondary: 11R21: Other number fields 11R29: Class numbers, class groups, discriminants
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 315 - 331
Copyright
© The Author(s) 2016 

References

Belabas, K., ‘Topics in computational algebraic number theory’, J. Théor. Nombres Bordeaux 16 (2004) 19–63.CrossRefGoogle Scholar
Biasse, J.-F. and Fieker, C., ‘Subexponential class group and unit group computation in large degree number fields’, LMS J. Comput. Math. 17 (2014) 385–403.Google Scholar
Buchmann, J., ‘A subexponential algorithm for the determination of class groups and regulators of algebraic number fields’, Séminaire de Théorie des Nombres, Paris 1988–1989 , Progress in Mathematics (ed. Goldstein, C.; Birkhäuser, Boston, 1990) 27–41.Google Scholar
‘Class Group Database’, http://www.mathematik.uni-kl.de/∼numberfieldtables/, maintained byG. Malle.Google Scholar
Cohen, H., A course in computational algebraic number theory , Graduate Texts in Mathematics 183 (Springer, Berlin, 1991).Google Scholar
Cohen, H. and Diaz y Diaz, F., ‘A polynomial reduction algorithm’, J. Théor. Nombres Bordeaux 3 (1991) 351–360.CrossRefGoogle Scholar
Gan, Y. H., Ling, C. and Mow, W. H., ‘Complex lattice reduction algorithm for low-complexity full-diversity MIMO detection’, IEEE Trans. Signal Process. 57 (2009) no. 7, 2701–2710.Google Scholar
Hafner, J. L. and McCurley, K. S., ‘A rigorous subexponential algorithm for computation of class groups’, J. Amer. Math. Soc. 2 (1989) 839–850.Google Scholar
Hanrot, G. and Stehlé, D., ‘Improved analysis of Kannan’s shortest lattice vector algorithm’, Advances in Cryptology – CRYPTO 2007 , Lecture Notes in Computer Science 4622 (ed. Menezes, A.; Springer, Berlin, 2007) 170–186.Google Scholar
Lehmer, D. H., ‘Factorization of certain cyclotomic functions’, Ann. of Math. (2) 34 (1933) 461–479.Google Scholar
Mahler, K., ‘An application of Jensen’s formula to polynomials’, J. Lond. Math. Soc. (2) 7 (1960) 98–100.Google Scholar
Mahler, K., ‘An inequality for the discriminant of a polynomial’, Michigan Math. J. 11 (1964) 257–262.Google Scholar
Mignotte, M. and Glesser, P., ‘Landau’s inequality via Hadmard’s’, J. Symbolic Comput. 18 (1994) 379–383.Google Scholar
Pohst, M. E., Computational algebraic number theory , DMV Lecture Notes 21 (Birkhäuser, Basel, 1993).CrossRefGoogle Scholar
Shanks, D., ‘Class number, a theory of factorization, and genera’, 1969 Number Theory Institute , Proceedings of Symposia in Pure Mathematics 20 (American Mathematical Society, Providence, RI, 1969) 415–440.Google Scholar
Shanks, D., ‘The infrastructure of a real quadratic field and its applications’, Proceedings of the 1972 Number Theory Conference (University of Colorado, Boulder, 1972) 217–224.Google Scholar