No CrossRef data available.
Article contents
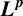$\boldsymbol {L}^{\boldsymbol {p}}$–
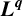$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
Part of:
Abstract harmonic analysis
Harmonic analysis in one variable
Harmonic analysis in several variables
Published online by Cambridge University Press: 18 October 2023
Abstract
The main purpose of this paper is to prove Hörmander’s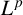 
$L^p$–
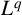$L^q$ boundedness of Fourier multipliers on commutative hypergroups. We carry out this objective by establishing the Paley inequality and Hausdorff–Young–Paley inequality for commutative hypergroups. We show the 
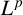$L^p$–
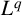$L^q$ boundedness of the spectral multipliers for the generalised radial Laplacian by examining our results on Chébli–Trimèche hypergroups. As a consequence, we obtain embedding theorems and time asymptotics for the 
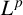$L^p$–
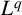$L^q$ norms of the heat kernel for generalised radial Laplacian.
Keywords
MSC classification
Primary:
43A62: Hypergroups
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 115 , Issue 3 , December 2023 , pp. 375 - 395
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Ji Li
The authors are supported by FWO Odysseus 1 Grant G.0H94.18N: Analysis and Partial Differential Equations, the Methusalem programme of the Ghent University Special Research Fund (BOF) (Grant number 01M01021) and by FWO Senior Research Grant G011522N. MR is also supported by the EPSRC Grant EP/R003025/2 and by the FWO Grant G022821N.
References
Akylzhanov, R., Majid, S. and Ruzhansky, M., ‘Smooth dense subalgebras and Fourier multipliers on compact quantum groups’, Comm. Math. Phys. 362(3) (2018), 761–799.CrossRefGoogle Scholar
Akylzhanov, R., Nursultanov, E. and Ruzhansky, M., ‘Hardy–Littlewood–Paley inequalities and Fourier multipliers on
$\mathrm{SU}(2)$
’, Studia Math. 234(1) (2016), 1–29.CrossRefGoogle Scholar
$\mathrm{SU}(2)$
’, Studia Math. 234(1) (2016), 1–29.CrossRefGoogle ScholarAkylzhanov, R., Nursultanov, E. and Ruzhansky, M., ‘Hardy–Littlewood, Hausdorff–Young–Paley inequalities, and
${L}^p-{L}^q$
Fourier multipliers on compact homogeneous manifolds’, J. Math. Anal. Appl. 479(2) (2019), 1519–1548.CrossRefGoogle Scholar
${L}^p-{L}^q$
Fourier multipliers on compact homogeneous manifolds’, J. Math. Anal. Appl. 479(2) (2019), 1519–1548.CrossRefGoogle ScholarAkylzhanov, R. and Ruzhansky, M., ‘
${L}^p-{L}^q$
multipliers on locally compact groups’, J. Funct. Anal. 278(3) (2020), 108324; doi:10.1016/j.jfa.2019.108324.CrossRefGoogle Scholar
${L}^p-{L}^q$
multipliers on locally compact groups’, J. Funct. Anal. 278(3) (2020), 108324; doi:10.1016/j.jfa.2019.108324.CrossRefGoogle ScholarAmini, M. and Chu, C.-H., ‘Harmonic functions on hypergroups’, J. Funct. Anal. 261(7) (2011), 1835–1864.CrossRefGoogle Scholar
Anker, J.-P., ‘Fourier multipliers on Riemannian symmetric spaces of the noncompact type’, Ann. of Math. (2) 132(3) (1990), 597–628.CrossRefGoogle Scholar
Anker, J.-P., Damek, E. and Yacoub, C., ‘Spherical analysis on harmonic AN groups’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 23(4) (1996), 643–679.Google Scholar
Baccar, C., Ben Hamadi, N. and Omri, S., ‘Fourier multipliers associated with singular partial differential operators’, Oper. Matrices 11(1) (2017), 37–53.CrossRefGoogle Scholar
Bergh, J. and Lofstrom, J., Interpolation Spaces, Grundlehren der mathematischen Wissenschaften, 223 (Springer, Berlin–Heidelberg, 1976).CrossRefGoogle Scholar
Betancor, J. J., Castro, A. J. and Curbelo, J., ‘Spectral multipliers for multidimensional Bessel operators’, J. Fourier Anal. Appl. 17(5) (2011), 932–975.CrossRefGoogle Scholar
Biswas, K., Knieper, G. and Peyerimhoff, N., ‘The Fourier transform on harmonic manifolds of purely exponential volume growth’, J. Geom. Anal. 31 (2019), 126–163.CrossRefGoogle Scholar
Bloom, W. R. and Heyer, H., Harmonic Analysis on Probability Measures on Hypergroups (De Gruyter, Berlin, 1995).CrossRefGoogle Scholar
Bloom, W. R. and Xu, Z., ‘The Hardy–Littlewood maximal function for Chébli–Trimèche hypergroups’, in: Applications of Hypergroups and Related Measure Algebras (Seattle, WA, 1993), Contemporary Mathematics, 183 (eds. Connett, W. C., Gebuhrer, M.-O. and Schwartz, A. L.) (American Mathematical Society, Providence, RI, 1995), 45–70.CrossRefGoogle Scholar
Bloom, W. R. and Xu, Z., ‘Fourier multipliers for local Hardy spaces on Chébli–Trimèche hypergroups’, Canad. J. Math. 50(5) (1998), 897–928.CrossRefGoogle Scholar
Bloom, W. R. and Xu, Z., ‘Fourier multipliers for
${L}^p$
on Chébli–Trimèche hypergroups’, Proc. Lond. Math. Soc. (3) 80(3) (2000), 643–664.CrossRefGoogle Scholar
${L}^p$
on Chébli–Trimèche hypergroups’, Proc. Lond. Math. Soc. (3) 80(3) (2000), 643–664.CrossRefGoogle ScholarCardona, D., Kumar, V., Ruzhansky, M. and Tokmagambetov, N., ‘
${L}^p$
–
${L}^q$
boundedness of pseudo-differential operators on smooth manifolds and its applications to nonlinear equations’, Preprint, 2020, arXiv:2005.04936.Google Scholar
${L}^p$
–
${L}^q$
boundedness of pseudo-differential operators on smooth manifolds and its applications to nonlinear equations’, Preprint, 2020, arXiv:2005.04936.Google ScholarChatzakou, M. and Kumar, V., ‘
${L}^p$
–
${L}^q$
boundedness of Fourier multipliers associated with the anharmonic oscillator’, Preprint, 2021, arXiv:2004.07801.Google Scholar
${L}^p$
–
${L}^q$
boundedness of Fourier multipliers associated with the anharmonic oscillator’, Preprint, 2021, arXiv:2004.07801.Google ScholarChatzakou, M. and Kumar, V., ‘
${L}^p-{L}^q$
boundedness of spectral multipliers of the anharmonic oscillator’, C. R. Math. Acad. Sci. Paris 360 (2022), 343–347.Google Scholar
${L}^p-{L}^q$
boundedness of spectral multipliers of the anharmonic oscillator’, C. R. Math. Acad. Sci. Paris 360 (2022), 343–347.Google ScholarChébli, H., ‘Generalized translation operators and convolution semi-groups’, in:
Theory of Potential and Harmonic Analysis (Journées Soc. Mat. France, Institute for Advanced Mathematical Research, Strasbourg, 1973), Reading Notes in Mathematics, 404 (ed. J. Faraut) (Springer, Berlin, 1974), 35–59 (in English).Google Scholar
Cowling, M., Giulini, S. and Meda, S., ‘
${L}^p$
–
${L}^q$
estimates for functions of the Laplace–Beltrami operator on noncompact symmetric spaces. I’, Duke Math. J. 72(1) (1993), 109–150.CrossRefGoogle Scholar
${L}^p$
–
${L}^q$
estimates for functions of the Laplace–Beltrami operator on noncompact symmetric spaces. I’, Duke Math. J. 72(1) (1993), 109–150.CrossRefGoogle ScholarDegenfeld-Schonburg, S., ‘On the Hausdorff–Young theorem for commutative hypergroups’, Colloq. Math. 131(2) (2013), 219–231.CrossRefGoogle Scholar
Delgado, J. and Ruzhansky, M., ‘Fourier multipliers, symbols, and nuclearity on compact manifolds’, J. Anal. Math. 135(2) (2018), 757–800.CrossRefGoogle Scholar
Dziubanśki, J. and Hejna, A., ‘Hor̈mander’s multiplier theorem for the Dunkl transform’, J. Funct. Anal. 277(7) (2019), 2133–2159.CrossRefGoogle Scholar
Dziubanśki, J., Preisner, M. and Wrob́el, B., ‘Multivariate Hor̈mander-type multiplier theorem for the Hankel transform’, J. Fourier Anal. Appl. 19(2) (2013), 417–437.CrossRefGoogle Scholar
Gosselin, J. and Stempak, K., ‘A weak-type estimate for Fourier–Bessel multipliers’, Proc. Amer. Math. Soc. 106(3) (1989), 655–662.CrossRefGoogle Scholar
Hörmander, L., ‘Estimates for translation invariant operators in
${L}^p$
spaces’, Acta Math. 104 (1960), 93–140.CrossRefGoogle Scholar
${L}^p$
spaces’, Acta Math. 104 (1960), 93–140.CrossRefGoogle ScholarJewett, R. I., ‘Space with an abstract convolution of measures’, Adv. Math. 18 (1975), 1–101.CrossRefGoogle Scholar
Koornwinder, T. H., ‘Jacobi functions and analysis on noncompact semisimple Lie groups’, in: Special Functions: Group Theoretical Aspects and Applications (eds. Askey, R. A., Koornwinder, T. H. and Schempp, W.) (Springer, Dordrecht, 1984), 1–85.Google Scholar
Kumar, V., Ross, K. A. and Singh, A. I., ‘Hypergroup deformations of semigroups’, Semigroup Forum 99(1) (2019), 169–195.CrossRefGoogle Scholar
Kumar, V., Ross, K. A. and Singh, A. I., ‘An addendum to hypergroup deformations of semigroups’, Semigroup Forum 99(1) (2019), 196–197.CrossRefGoogle Scholar
Kumar, V., Ross, K. A. and Singh, A. I., ‘Ramsey theory for hypergroups’, Semigroup Forum 100(2) (2020), 482–504.CrossRefGoogle Scholar
Kumar, V. and Ruzhansky, M., ‘Hardy–Littlewood inequality and
${L}^p$
–
${L}^q$
Fourier multipliers on compact hypergroups’, J. Lie theory 32(2) (2022), 475–498.Google Scholar
${L}^p$
–
${L}^q$
Fourier multipliers on compact hypergroups’, J. Lie theory 32(2) (2022), 475–498.Google ScholarKumar, V. and Ruzhansky, M., ‘
${L}^p$
–
${L}^q$
boundedness of
$\left(k,a\right)$
-Fourier multipliers with applications to nonlinear equations’, Int. Math. Res. Not. IMRN 2 (2023), 1073–1093.CrossRefGoogle Scholar
${L}^p$
–
${L}^q$
boundedness of
$\left(k,a\right)$
-Fourier multipliers with applications to nonlinear equations’, Int. Math. Res. Not. IMRN 2 (2023), 1073–1093.CrossRefGoogle ScholarKumar, V., Sarma, R. and Shravan Kumar, N., ‘Characterisation of multipliers on hypergroups’, Acta Math. Vietnam. 45 (2020), 783–794.CrossRefGoogle Scholar
Majjaouli, B. and Omri, S., ‘Estimate of the Fourier multipliers in the spherical mean setting’, J. Pseudo-Differ. Oper. Appl. 8(3) (2017), 533–549.CrossRefGoogle Scholar
Michael, E., ‘Topologies on spaces of subsets’, Trans. Amer. Math. Soc. 71 (1951), 152–182.CrossRefGoogle Scholar
Ruzhansky, M. and Wirth, J., ‘
${L}^p$
Fourier multipliers on compact Lie groups’, Math. Z. 280(3–4) (2015), 621–642.CrossRefGoogle Scholar
${L}^p$
Fourier multipliers on compact Lie groups’, Math. Z. 280(3–4) (2015), 621–642.CrossRefGoogle ScholarSarma, R., Shravan Kumar, N. and Kumar, V., ‘Multipliers in vector-valued
${L}^1$
-spaces for hypergroups’, Acta Math. Sin. (Engl. Ser.) 34(7) (2018), 1059–1073.CrossRefGoogle Scholar
${L}^1$
-spaces for hypergroups’, Acta Math. Sin. (Engl. Ser.) 34(7) (2018), 1059–1073.CrossRefGoogle ScholarSoltani, F., ‘
${L}^p$
-Fourier multipliers for the Dunkl operator on the real line’,
J. Funct. Anal. 209(1) (2004), 16–35.CrossRefGoogle Scholar
${L}^p$
-Fourier multipliers for the Dunkl operator on the real line’,
J. Funct. Anal. 209(1) (2004), 16–35.CrossRefGoogle ScholarStempak, K., ‘La théorie de Littlewood–Paley pour la transformation de Fourier–Bessel’, C. R. Math. Acad. Sci. Paris 303 (1986), 15–18.Google Scholar
Trimèche, K., ‘Transformation intègrale de Weyl et thèorème de Paley–Wiener associés à un opérateur différentiel singulier sur
$\left(0,\infty \right)$
(in French) [Weyl integral transform and Paley–Wiener theorem associated with a singular differential operator on
$\left(0,\infty \right)$
]’, J. Math. Pures Appl. (9) 60(1) (1981), 51–98.Google Scholar
$\left(0,\infty \right)$
(in French) [Weyl integral transform and Paley–Wiener theorem associated with a singular differential operator on
$\left(0,\infty \right)$
]’, J. Math. Pures Appl. (9) 60(1) (1981), 51–98.Google ScholarWróbel, B., ‘Multivariate spectral multipliers for the Dunkl transform and the Dunkl harmonic oscillator’, Forum Math. 27(4) (2015), 2301–2322.CrossRefGoogle Scholar
Youn, S.-G., ‘Hardy–Littlewood inequalities on compact quantum groups of Kac type’, Anal. PDE 11(1) (2018), 237–261.CrossRefGoogle Scholar