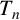1 Introduction
It is well known that congruences on a group G and normal subgroups of G are essentially the same. Thus, every congruence on G is completely determined by the equivalence class of the identity element
![]() $1\in G$
, this equivalence class is always a normal subgroup of G, and every normal subgroup N of G is the identity element equivalence class of a congruence on G (namely, the smallest congruence on G containing
$1\in G$
, this equivalence class is always a normal subgroup of G, and every normal subgroup N of G is the identity element equivalence class of a congruence on G (namely, the smallest congruence on G containing
![]() $\{1\}\times N$
). In other words, there is a canonical bijection
$\{1\}\times N$
). In other words, there is a canonical bijection
mapping every congruence R to the equivalence class
![]() $[1]_R$
whose inverse
$[1]_R$
whose inverse
maps each normal subgroup N to the unique congruence
![]() $R_N$
such that
$R_N$
such that
![]() $[1]_{R_N}=N$
and whose equivalence classes are the (left or right) cosets of G modulo N. In fact, both
$[1]_{R_N}=N$
and whose equivalence classes are the (left or right) cosets of G modulo N. In fact, both
![]() $\Psi _G$
and
$\Psi _G$
and
![]() $\Phi _G$
are lattice isomorphisms when the domain and the codomain are ordered by inclusion. Indeed, both
$\Phi _G$
are lattice isomorphisms when the domain and the codomain are ordered by inclusion. Indeed, both
![]() $\Psi _G$
and
$\Psi _G$
and
![]() $\Phi _G$
are order-preserving, and every order-preserving bijection between lattices with an order-preserving inverse automatically preserves joins and meets because the lattice operations can be defined in terms of the ordering.
$\Phi _G$
are order-preserving, and every order-preserving bijection between lattices with an order-preserving inverse automatically preserves joins and meets because the lattice operations can be defined in terms of the ordering.
As it is also well known, things are not so simple for arbitrary monoids. In fact, the equivalence class of the identity element modulo a congruence no longer determines the congruence. Thus, if M is a monoid and I is any ideal of M (a nonempty subset I such that
![]() $MIM\subseteq I$
), the equivalence relation
$MIM\subseteq I$
), the equivalence relation
![]() $R_I$
on M given by
$R_I$
on M given by
is a congruence, called the Rees congruence of I. It follows that for every proper ideal I of M, the congruence
![]() $R_I$
is what we call a unital congruence, that is, a congruence R such that
$R_I$
is what we call a unital congruence, that is, a congruence R such that
![]() $[1]_{R}=\{1\}$
. In general, these are not the only unital congruences on a monoid. Otherwise, finding all congruences on a given monoid is much easier, as becomes clear in the following (compare with Theorem 3.15 below). For instance, if M is the additive monoid
$[1]_{R}=\{1\}$
. In general, these are not the only unital congruences on a monoid. Otherwise, finding all congruences on a given monoid is much easier, as becomes clear in the following (compare with Theorem 3.15 below). For instance, if M is the additive monoid
![]() $\mathbb {N}_+=(\mathbb {N},+,0)$
, it is easy to check that
$\mathbb {N}_+=(\mathbb {N},+,0)$
, it is easy to check that
is a congruence on
![]() $\mathbb {N}_+$
for each
$\mathbb {N}_+$
for each
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $n\geq 1$
. In particular, all congruences
$n\geq 1$
. In particular, all congruences
![]() $R_{m,n}$
with
$R_{m,n}$
with
![]() $m>0$
are unital, but only the congruences
$m>0$
are unital, but only the congruences
![]() $R_{m,1}$
for every
$R_{m,1}$
for every
![]() $m>0$
are Rees congruences.
$m>0$
are Rees congruences.
The main purpose of this paper is to prove a weaker version of the above lattice isomorphism
![]() $\mathsf {NorSub}(G)\cong \mathsf {Cong}(G)$
that holds true for arbitrary monoids, and to discuss a strategy for computing the lattice of congruences of a monoid that follows from it. The key notion is that of a normal submonoid of a monoid. It plays the role of a normal subgroup of a group.
$\mathsf {NorSub}(G)\cong \mathsf {Cong}(G)$
that holds true for arbitrary monoids, and to discuss a strategy for computing the lattice of congruences of a monoid that follows from it. The key notion is that of a normal submonoid of a monoid. It plays the role of a normal subgroup of a group.
The paper is organized as follows. In Section 2, a notion of normal submonoids of a monoid M is introduced that we argue plays the role of the normal subgroups of a group. Thus, we see that the preimage
![]() $f^{-1}(1)$
for every monoid homomorphism
$f^{-1}(1)$
for every monoid homomorphism
![]() $f:M\to N$
, and the equivalence class of the identity element
$f:M\to N$
, and the equivalence class of the identity element
![]() $1\in M$
modulo any congruence on M are both normal submonoids of M in our sense (Propositions 2.8 and 3.5, respectively), and that every normal submonoid of M is the preimage
$1\in M$
modulo any congruence on M are both normal submonoids of M in our sense (Propositions 2.8 and 3.5, respectively), and that every normal submonoid of M is the preimage
![]() $f^{-1}(1)$
of some monoid homomorphism
$f^{-1}(1)$
of some monoid homomorphism
![]() $f:M\to N$
(Corollary 3.8). As expected, the set
$f:M\to N$
(Corollary 3.8). As expected, the set
![]() $\mathsf {NorSub}(M)$
of normal submonoids of a monoid M, when ordered by inclusion, is a lattice with meets and joins respectively given by the intersection and the normal closure of the union. The normal closure of an arbitrary subset A of the monoid is explicitly described in terms of A (Proposition 2.15). As an example, the lattice
$\mathsf {NorSub}(M)$
of normal submonoids of a monoid M, when ordered by inclusion, is a lattice with meets and joins respectively given by the intersection and the normal closure of the union. The normal closure of an arbitrary subset A of the monoid is explicitly described in terms of A (Proposition 2.15). As an example, the lattice
![]() $\mathsf {NorSub}(T_n)$
of the finite full transformation monoids
$\mathsf {NorSub}(T_n)$
of the finite full transformation monoids
![]() $T_n$
is computed for each
$T_n$
is computed for each
![]() $n\geq 1$
. In particular, it is shown that
$n\geq 1$
. In particular, it is shown that
![]() $T_n$
is ‘normally simple’, that is, such that its only proper normal submonoids are the normal subgroups of its group of units (Proposition 2.22). The modularity of the lattice
$T_n$
is ‘normally simple’, that is, such that its only proper normal submonoids are the normal subgroups of its group of units (Proposition 2.22). The modularity of the lattice
![]() $\mathsf {NorSub}(M)$
is shown for a particular type of monoid, including all free commutative monoids and, more generally, all Krull monoids (Theorem 2.27 and Example 2.28). In Section 3, a weakening is shown of the lattice isomorphism
$\mathsf {NorSub}(M)$
is shown for a particular type of monoid, including all free commutative monoids and, more generally, all Krull monoids (Theorem 2.27 and Example 2.28). In Section 3, a weakening is shown of the lattice isomorphism
![]() $\mathsf {NorSub}(G)\cong \mathsf {Cong}(G)$
that holds for arbitrary monoids. More specifically, it is shown that for every monoid M, the map
$\mathsf {NorSub}(G)\cong \mathsf {Cong}(G)$
that holds for arbitrary monoids. More specifically, it is shown that for every monoid M, the map
![]() $\Phi _M:\mathsf {NorSub}(M)\to \mathsf {Cong}(M)$
sending each normal submonoid S of M to the smallest congruence
$\Phi _M:\mathsf {NorSub}(M)\to \mathsf {Cong}(M)$
sending each normal submonoid S of M to the smallest congruence
![]() $R_S$
on M containing
$R_S$
on M containing
![]() $\{1\}\times S$
is join-preserving, and is a one-to-one map with a left inverse given by the map
$\{1\}\times S$
is join-preserving, and is a one-to-one map with a left inverse given by the map
![]() $\Psi _M:\mathsf {Cong}(M)\to \mathsf {NorSub}(M)$
sending each congruence to the equivalence class of the identity element (Theorem 3.6). This leads to a possible strategy to compute the lattice of congruences on a monoid M, which essentially consists of finding the lattice of normal submonoids of M, and the lattices of unital congruences on the so-called ‘normal quotients’ of M, that is, the quotients of M modulo the congruences in the image of
$\Psi _M:\mathsf {Cong}(M)\to \mathsf {NorSub}(M)$
sending each congruence to the equivalence class of the identity element (Theorem 3.6). This leads to a possible strategy to compute the lattice of congruences on a monoid M, which essentially consists of finding the lattice of normal submonoids of M, and the lattices of unital congruences on the so-called ‘normal quotients’ of M, that is, the quotients of M modulo the congruences in the image of
![]() $\Phi _M$
(Theorem 3.15). This way, the problem of computing the congruences on the monoids reduces to just computing the unital ones. This strategy provides a new perspective on the classical theorem by Malcev describing all congruences on the finite full transformation monoids [Reference Malcev10], and it shows that these monoids are ‘congruentially simple’, that is, such that all congruences are completely determined by the equivalence class of the identity element except when this class reduces to
$\Phi _M$
(Theorem 3.15). This way, the problem of computing the congruences on the monoids reduces to just computing the unital ones. This strategy provides a new perspective on the classical theorem by Malcev describing all congruences on the finite full transformation monoids [Reference Malcev10], and it shows that these monoids are ‘congruentially simple’, that is, such that all congruences are completely determined by the equivalence class of the identity element except when this class reduces to
![]() $\{1\}$
. Although this result is an easy consequence of the Malcev theorem, we prove it without using this theorem.
$\{1\}$
. Although this result is an easy consequence of the Malcev theorem, we prove it without using this theorem.
Note. One week before finishing this work, Martins-Ferreira and Sobral put on the web a preprint [Reference Martins-Ferreira and Sobral11] where the same notion of normal submonoid is used. In Remark 1 of this preprint, the authors mention a paper by Facchini and Rodaro [Reference Facchini and Rodaro6] where this notion seems to be introduced for the first time. The present work has been done completely independently from both papers.
2 Normal submonoids of a monoid
In what follows,
![]() $M=(M,\cdot ,1)$
stands for a monoid and
$M=(M,\cdot ,1)$
stands for a monoid and
![]() $U(M)$
for its group of units (that is, the elements
$U(M)$
for its group of units (that is, the elements
![]() $x\in M$
having a two-sided inverse
$x\in M$
having a two-sided inverse
![]() $x^{-1}\in M$
). For every subset
$x^{-1}\in M$
). For every subset
![]() $T\subseteq M$
, we denote by
$T\subseteq M$
, we denote by
![]() $\langle T\rangle $
the smallest submonoid containing T. Thus,
$\langle T\rangle $
the smallest submonoid containing T. Thus,
![]() $\langle T\rangle $
consists of all finite products of elements in T, including the empty product (equal to
$\langle T\rangle $
consists of all finite products of elements in T, including the empty product (equal to
![]() $1$
by convention). If M is commutative, we use additive notation. In particular, the identity element is denoted by
$1$
by convention). If M is commutative, we use additive notation. In particular, the identity element is denoted by
![]() $0$
instead of
$0$
instead of
![]() $1$
.
$1$
.
2.1 Groupal, invariant, and normal submonoids
By a subgroup of a monoid M, it is usually meant a subsemigroup (that is, a nonempty subset closed with respect to
![]() $\cdot $
) which is a group with the induced binary operation. Notice that the identity element of a generic subgroup of M need not coincide with the identity
$\cdot $
) which is a group with the induced binary operation. Notice that the identity element of a generic subgroup of M need not coincide with the identity
![]() $1$
of M so that a generic subgroup of M need not be a submonoid. For instance, for every idempotent
$1$
of M so that a generic subgroup of M need not be a submonoid. For instance, for every idempotent
![]() $e\neq 1$
of M, the set
$e\neq 1$
of M, the set
![]() $\{e\}$
is a subgroup of M but not a submonoid.
$\{e\}$
is a subgroup of M but not a submonoid.
Together with this notion, however, there is also the following one, of more interest to us, which also reduces to the notion of a subgroup when M is a group.
Definition 2.1. A groupal submonoid of M is a submonoid
![]() $S\subseteq M$
closed under inverses, that is, such that
$S\subseteq M$
closed under inverses, that is, such that
![]() $x^{-1}\in S$
for each
$x^{-1}\in S$
for each
![]() $x\in S\cap U(M)$
.
$x\in S\cap U(M)$
.
Clearly, every subgroup H of
![]() $U(M)$
is a groupal submonoid, but the converse is false in general. Thus, if
$U(M)$
is a groupal submonoid, but the converse is false in general. Thus, if
![]() $U(M)=\{1\}$
(for instance, if M is the additive monoid
$U(M)=\{1\}$
(for instance, if M is the additive monoid
![]() $\mathbb {N}_+=(\mathbb {N},+,0)$
of natural numbers), every nontrivial submonoid of M is automatically a groupal submonoid not included in
$\mathbb {N}_+=(\mathbb {N},+,0)$
of natural numbers), every nontrivial submonoid of M is automatically a groupal submonoid not included in
![]() $U(M)$
. However, in a generic monoid, there are submonoids that are not groupal. For instance, for every
$U(M)$
. However, in a generic monoid, there are submonoids that are not groupal. For instance, for every
![]() $n\times n$
invertible matrix A whose inverse is not a power of itself, the subset
$n\times n$
invertible matrix A whose inverse is not a power of itself, the subset
![]() $\{A^k : k\geq 0\}$
is a submonoid of the multiplicative monoid
$\{A^k : k\geq 0\}$
is a submonoid of the multiplicative monoid
![]() $M_n(k)$
of all
$M_n(k)$
of all
![]() $n\times n$
matrices but not a groupal submonoid.
$n\times n$
matrices but not a groupal submonoid.
For every subset
![]() $T\subseteq M$
, we denote by
$T\subseteq M$
, we denote by
![]() $\langle T\rangle '$
the smallest groupal submonoid containing T (equivalently, the intersection of all groupal submonoids containing T). In general, it is different from the submonoid
$\langle T\rangle '$
the smallest groupal submonoid containing T (equivalently, the intersection of all groupal submonoids containing T). In general, it is different from the submonoid
![]() $\langle T\rangle $
generated by T because it consists of all finite products of elements of T and/or their inverses (when invertible). For instance, if
$\langle T\rangle $
generated by T because it consists of all finite products of elements of T and/or their inverses (when invertible). For instance, if
![]() $M=M_2(\mathbb {R})$
, then
$M=M_2(\mathbb {R})$
, then
 $$ \begin{align*} \left\langle \left(\begin{array}{cc} 1&0\\0&2\end{array}\right)\right\rangle=\left\{\left(\begin{array}{cc} 1&0\\0&2\end{array}\right)^k : k\geq 0\right\}, \end{align*} $$
$$ \begin{align*} \left\langle \left(\begin{array}{cc} 1&0\\0&2\end{array}\right)\right\rangle=\left\{\left(\begin{array}{cc} 1&0\\0&2\end{array}\right)^k : k\geq 0\right\}, \end{align*} $$
while
 $$ \begin{align*} \left\langle \left(\begin{array}{cc} 1&0\\0&2\end{array}\right)\right\rangle'=\left\{\left(\begin{array}{cc} 1&0\\0&2\end{array}\right)^k : k\in\mathbb{Z}\right\}. \end{align*} $$
$$ \begin{align*} \left\langle \left(\begin{array}{cc} 1&0\\0&2\end{array}\right)\right\rangle'=\left\{\left(\begin{array}{cc} 1&0\\0&2\end{array}\right)^k : k\in\mathbb{Z}\right\}. \end{align*} $$
Actually, we are interested in the analog for monoids of the normal subgroups of a group. We want them to be a particular type of submonoid such that the equivalence class of the identity element modulo any congruence is of this type. At first sight, we might be tempted to take as our analog the groupal submonoids S that are invariant under conjugation by arbitrary invertible elements in M (that is, such that
![]() $xSx^{-1}\subseteq S$
for every
$xSx^{-1}\subseteq S$
for every
![]() $x\in U(M)$
) or, more generally, such that
$x\in U(M)$
) or, more generally, such that
![]() $xSy\subseteq S$
for each
$xSy\subseteq S$
for each
![]() $x,y\in M$
such that
$x,y\in M$
such that
![]() $xy\in S$
. For every congruence, the equivalence class of the identity element indeed satisfies this condition. However, this condition turns out to be too weak if we also want every ‘normal submonoid’ to be the identity element equivalence class modulo some congruence on M, as is the case for the normal subgroups of a group. In fact, if S is invariant in this sense, it may happen that the smallest congruence R on M for which
$xy\in S$
. For every congruence, the equivalence class of the identity element indeed satisfies this condition. However, this condition turns out to be too weak if we also want every ‘normal submonoid’ to be the identity element equivalence class modulo some congruence on M, as is the case for the normal subgroups of a group. In fact, if S is invariant in this sense, it may happen that the smallest congruence R on M for which
![]() $S\subseteq [1]_R$
is a congruence such that
$S\subseteq [1]_R$
is a congruence such that
![]() $S\neq [1]_R$
. If so, there is no congruence with S as the equivalence class of
$S\neq [1]_R$
. If so, there is no congruence with S as the equivalence class of
![]() $1$
. The fact that this can indeed happen becomes clear in the following. As argued below, the right notion of invariance turns out to be as follows.
$1$
. The fact that this can indeed happen becomes clear in the following. As argued below, the right notion of invariance turns out to be as follows.
Definition 2.2. A subset
![]() $A\subseteq M$
is called invariant if for each
$A\subseteq M$
is called invariant if for each
![]() $x,y\in M$
, the following conditions are equivalent:
$x,y\in M$
, the following conditions are equivalent:
-
(i)
 $xAy\subseteq A$
;
$xAy\subseteq A$
; -
(ii)
 $xy\in A$
;
$xy\in A$
; -
(iii)
 $(xAy)\cap A\neq \emptyset $
.
$(xAy)\cap A\neq \emptyset $
.
It is worth introducing the (two-sided) ‘stability set’ of any subset A, and its generalized conjugates, and to restate the invariance condition of a submonoid in terms of it.
Definition 2.3. The (two-sided) stability set (relative to M) of a subset
![]() $A\subseteq M$
is the set
$A\subseteq M$
is the set
The subsets
![]() $xAy$
for each
$xAy$
for each
![]() $(x,y)\in X_A$
are called the generalized conjugates of A (in M).
$(x,y)\in X_A$
are called the generalized conjugates of A (in M).
It readily follows from the definition that
![]() $X_A\subseteq X_{B}$
if
$X_A\subseteq X_{B}$
if
![]() $A\subseteq B$
. Moreover, for a submonoid S, the stability set
$A\subseteq B$
. Moreover, for a submonoid S, the stability set
![]() $X_S$
contains
$X_S$
contains
![]() $S\times S$
as well as the set
$S\times S$
as well as the set
![]() $\{(x,x^{-1}) : x\in U(M)\}$
. This is why the subsets
$\{(x,x^{-1}) : x\in U(M)\}$
. This is why the subsets
![]() $xAy$
for each
$xAy$
for each
![]() $(x,y)\in X_A$
are called the generalized conjugates of A: when A is a submonoid S, they include the usual conjugates
$(x,y)\in X_A$
are called the generalized conjugates of A: when A is a submonoid S, they include the usual conjugates
![]() $xSx^{-1}$
of S for each
$xSx^{-1}$
of S for each
![]() $x\in U(M)$
. In general, however,
$x\in U(M)$
. In general, however,
![]() $X_S$
contains many pairs other than these. For instance,
$X_S$
contains many pairs other than these. For instance,
and the equation
![]() $xy=1$
may have solutions that are neither in
$xy=1$
may have solutions that are neither in
![]() $S\times S$
nor of the form
$S\times S$
nor of the form
![]() $(x,x^{-1})$
for some
$(x,x^{-1})$
for some
![]() $x\in U(M)$
. Finally, let us remark that when M is commutative,
$x\in U(M)$
. Finally, let us remark that when M is commutative,
![]() $X_S$
is a submonoid of
$X_S$
is a submonoid of
![]() $M\times M$
(containing the submonoid
$M\times M$
(containing the submonoid
![]() $S\times S$
).
$S\times S$
).
In terms of the stability set, and the generalized conjugates, the invariance condition on a submonoid S can be restated as follows.
Proposition 2.4. A submonoid
![]() $S\subseteq M$
is invariant if and only if
$S\subseteq M$
is invariant if and only if
that is, if and only if all of its generalized conjugates are subsets of itself.
Proof. If A is a submonoid S, not just a subset, condition (i) in the definition of invariant subset implies condition (ii) because
![]() $xy=xey\in A$
, and condition (ii) implies condition (iii) because
$xy=xey\in A$
, and condition (ii) implies condition (iii) because
![]() $xy=xey\in (xAy)\cap A$
. Hence, conditions (i)–(iii) are equivalent if and only if condition (iii) implies condition (i).
$xy=xey\in (xAy)\cap A$
. Hence, conditions (i)–(iii) are equivalent if and only if condition (iii) implies condition (i).
Notice that every submonoid satisfying Equation (2-1) is invariant in the previous weaker sense, but not conversely. For instance, a submonoid of a monoid with a trivial group of units is automatically invariant in the weak sense, but not necessarily in our stronger sense. An example is provided by the monoid
![]() $\mathbb {N}_+$
(see Proposition 2.9 below). This leads us to the following analog for arbitrary monoids of the normal subgroups of a group.
$\mathbb {N}_+$
(see Proposition 2.9 below). This leads us to the following analog for arbitrary monoids of the normal subgroups of a group.
Definition 2.5. A normal submonoid of a monoid M is a submonoid that is both groupal and invariant.
Remark 2.6. Usually, a submonoid S of a monoid M is called normal when
![]() $xS=Sx$
for each
$xS=Sx$
for each
![]() $x\in M$
. (For instance, this is the notion of ‘normal submonoid’ that appears in the groupprops webpage; see https://groupprops.subwiki.org/wiki/Normal_submonoid.) In fact, every subgroup H of
$x\in M$
. (For instance, this is the notion of ‘normal submonoid’ that appears in the groupprops webpage; see https://groupprops.subwiki.org/wiki/Normal_submonoid.) In fact, every subgroup H of
![]() $U(M)$
normal in this sense is a normal submonoid in our sense, as the reader may easily check. However, even restricting to subgroups H of
$U(M)$
normal in this sense is a normal submonoid in our sense, as the reader may easily check. However, even restricting to subgroups H of
![]() $U(M)$
, this condition is not equivalent to the invariance condition in Equation (2-1). For instance,
$U(M)$
, this condition is not equivalent to the invariance condition in Equation (2-1). For instance,
![]() $U(T_n)=S_n$
is a normal submonoid of
$U(T_n)=S_n$
is a normal submonoid of
![]() $T_n$
in our sense (see Proposition 2.19 below), but it is not true that
$T_n$
in our sense (see Proposition 2.19 below), but it is not true that
![]() $f\,S_n=S_n\,f$
for every transformation
$f\,S_n=S_n\,f$
for every transformation
![]() $f\in T_n$
if
$f\in T_n$
if
![]() $n>1$
(just take
$n>1$
(just take
![]() $n=2$
and f any constant map). The same problem persists with the (nonequivalent) condition
$n=2$
and f any constant map). The same problem persists with the (nonequivalent) condition
![]() $xSx^{-1}\subseteq S$
for each invertible element
$xSx^{-1}\subseteq S$
for each invertible element
![]() $x\in U(M)$
.
$x\in U(M)$
.
If S is a normal submonoid of M, we write
![]() $S\lhd M$
. Clearly, if
$S\lhd M$
. Clearly, if
![]() $S\lhd M$
and N is a submonoid of M containing S, then
$S\lhd M$
and N is a submonoid of M containing S, then
![]() $S\lhd N$
. However, a normal submonoid of a normal submonoid of M need not be a normal submonoid of M. In fact, this is already so when M is a group.
$S\lhd N$
. However, a normal submonoid of a normal submonoid of M need not be a normal submonoid of M. In fact, this is already so when M is a group.
The following results provide examples of normal submonoids. The first two show that our normal submonoids can be thought of as analogs for the generic monoids of the normal subgroups of a group. Additional arguments in favor of this viewpoint are discussed below. The third one highlights the difference between the submonoids
of
![]() $\mathbb {N}_+$
and all other submonoids of
$\mathbb {N}_+$
and all other submonoids of
![]() $\mathbb {N}_+$
.
$\mathbb {N}_+$
.
Proposition 2.7. The normal submonoids of a group G are the normal subgroups of G.
Proof. Let S be a normal submonoid of G, and let us suppose that for some
![]() $x\in G$
and
$x\in G$
and
![]() $s\in S$
, we have
$s\in S$
, we have
![]() $xsx^{-1}\notin S$
. Using the equivalence between conditions (ii) and (iii) with
$xsx^{-1}\notin S$
. Using the equivalence between conditions (ii) and (iii) with
![]() $y=sx^{-1}$
, we conclude that
$y=sx^{-1}$
, we conclude that
However,
![]() $e=xx^{-1}=xs^{-1}(sx^{-1})\in (xS(sx^{-1}))\cap S$
, contradicting our conclusion. Therefore,
$e=xx^{-1}=xs^{-1}(sx^{-1})\in (xS(sx^{-1}))\cap S$
, contradicting our conclusion. Therefore,
![]() $xSx^{-1}\subseteq S$
for every
$xSx^{-1}\subseteq S$
for every
![]() $x\in G$
. Conversely, let S be a normal subgroup of G. We have to see that S satisfies Equation (2-1). Indeed, let us suppose that
$x\in G$
. Conversely, let S be a normal subgroup of G. We have to see that S satisfies Equation (2-1). Indeed, let us suppose that
![]() $(xSy)\cap S\neq \emptyset $
for some
$(xSy)\cap S\neq \emptyset $
for some
![]() $x,y\in G$
. This means that there exist
$x,y\in G$
. This means that there exist
![]() $s_1,s_2\in S$
such that
$s_1,s_2\in S$
such that
![]() $xs_1y=s_2$
. Then for each
$xs_1y=s_2$
. Then for each
![]() $s\in S$
, we have
$s\in S$
, we have
![]() $xsy=\tilde {s}s_2$
with
$xsy=\tilde {s}s_2$
with
![]() $\tilde {s}=xss^{-1}x^{-1}$
. Now,
$\tilde {s}=xss^{-1}x^{-1}$
. Now,
![]() $\tilde {s}\in S$
because S is a normal subgroup of G. Hence,
$\tilde {s}\in S$
because S is a normal subgroup of G. Hence,
![]() $xsy\in S$
and
$xsy\in S$
and
![]() $xSy\subseteq S$
.
$xSy\subseteq S$
.
Proposition 2.8. Let
![]() $f:M\to N$
be a monoid homomorphism. Then
$f:M\to N$
be a monoid homomorphism. Then
![]() $f^{-1}(1)$
is a normal submonoid of M.
$f^{-1}(1)$
is a normal submonoid of M.
Proof. Clearly,
![]() $f^{-1}(1)$
is always a groupal submonoid of M. Suppose that for some
$f^{-1}(1)$
is always a groupal submonoid of M. Suppose that for some
![]() $x,y\in M$
, there exists
$x,y\in M$
, there exists
![]() $z_1,z_2\in f^{-1}(1)$
such that
$z_1,z_2\in f^{-1}(1)$
such that
![]() $xz_1y=z_2$
. Then
$xz_1y=z_2$
. Then
![]() $1_N=f(z_2)=f(xz_1y)=f(x)f(y)$
and hence, for every
$1_N=f(z_2)=f(xz_1y)=f(x)f(y)$
and hence, for every
![]() $z\in f^{-1}(1)$
, we have
$z\in f^{-1}(1)$
, we have
![]() $f(xzy)=f(x)f(y)=1_N$
, that is,
$f(xzy)=f(x)f(y)=1_N$
, that is,
![]() $x\,f^{-1}(1)\,y\subseteq f^{-1}(1)$
. Thus,
$x\,f^{-1}(1)\,y\subseteq f^{-1}(1)$
. Thus,
![]() $f^{-1}(1)$
is also invariant.
$f^{-1}(1)$
is also invariant.
Proposition 2.9. The normal submonoids of
![]() $\mathbb {N}_+$
are the submonoids in Equation (2-2).
$\mathbb {N}_+$
are the submonoids in Equation (2-2).
Proof. The submonoid
![]() $\langle n\rangle $
is clearly groupal. Moreover, if
$\langle n\rangle $
is clearly groupal. Moreover, if
![]() $(k,l)\in X_{\langle n\rangle }$
, there exist
$(k,l)\in X_{\langle n\rangle }$
, there exist
![]() $q,q'\geq 0$
such that
$q,q'\geq 0$
such that
![]() $k+nq+l=nq'$
. Hence,
$k+nq+l=nq'$
. Hence,
![]() $q'\geq q$
, and
$q'\geq q$
, and
![]() $k+l\in \langle n\rangle $
so that
$k+l\in \langle n\rangle $
so that
![]() $k+\langle n\rangle +l\subseteq \langle n\rangle $
, that is,
$k+\langle n\rangle +l\subseteq \langle n\rangle $
, that is,
![]() $\langle n\rangle $
is invariant. Let us now prove that these are the only normal submonoids of
$\langle n\rangle $
is invariant. Let us now prove that these are the only normal submonoids of
![]() $\mathbb {N}_+$
. Since all submonoids of
$\mathbb {N}_+$
. Since all submonoids of
![]() $\mathbb {N}_+$
are groupal, we need to show that these are the only invariant submonoids. To prove this, let S be any submonoid of
$\mathbb {N}_+$
are groupal, we need to show that these are the only invariant submonoids. To prove this, let S be any submonoid of
![]() $\mathbb {N}_+$
and
$\mathbb {N}_+$
and
![]() $n:=\min (S\setminus \{0\})$
, so that
$n:=\min (S\setminus \{0\})$
, so that
![]() $\langle n\rangle \subseteq S$
. If
$\langle n\rangle \subseteq S$
. If
![]() $S\neq \langle n\rangle $
, let
$S\neq \langle n\rangle $
, let
![]() $n':=\min (S\setminus \langle n\rangle )$
. Then we have
$n':=\min (S\setminus \langle n\rangle )$
. Then we have
![]() $n'=nq'+r$
for some
$n'=nq'+r$
for some
![]() $0<r<n$
and
$0<r<n$
and
![]() $q'\geq 1$
(
$q'\geq 1$
(
![]() $q' \neq 0$
because n is the least nonzero element of S). It follows that
$q' \neq 0$
because n is the least nonzero element of S). It follows that
![]() $n'\in (0+S+r)\cap S$
, that is,
$n'\in (0+S+r)\cap S$
, that is,
![]() $(0,r)\in X_S$
. However,
$(0,r)\in X_S$
. However, ![]() because
because
![]() $r\in 0+S+r$
while
$r\in 0+S+r$
while
![]() $r\notin S$
.
$r\notin S$
.
Remark 2.10. It follows from Proposition 2.9 that in a commutative monoid, not every groupal submonoid is necessarily invariant. For instance, the subset
![]() $S_n:=\{k : k\geq n\}\cup \{0\}\subseteq \mathbb {N}$
is a groupal submonoid of
$S_n:=\{k : k\geq n\}\cup \{0\}\subseteq \mathbb {N}$
is a groupal submonoid of
![]() $\mathbb {N}_+$
for each
$\mathbb {N}_+$
for each
![]() $n\geq 2$
but not a normal submonoid. Hence, the set (in fact, lattice) of normal submonoids of a generic commutative monoid does not coincide with the set of all submonoids, as occurs when the monoid is a group.
$n\geq 2$
but not a normal submonoid. Hence, the set (in fact, lattice) of normal submonoids of a generic commutative monoid does not coincide with the set of all submonoids, as occurs when the monoid is a group.
Let us finish this paragraph with two more examples of normal submonoids. The second example provides another case of a commutative monoid with groupal submonoids that are not invariant.
Example 2.11. Let
![]() $\mathbb {N}_{\max }$
be the set
$\mathbb {N}_{\max }$
be the set
![]() $\mathbb {N}$
of natural numbers equipped with the product given by
$\mathbb {N}$
of natural numbers equipped with the product given by
Here,
![]() $\mathbb {N}_{\max }$
is a commutative monoid with
$\mathbb {N}_{\max }$
is a commutative monoid with
![]() $0$
as identity element. We claim that
$0$
as identity element. We claim that
![]() $\{0,1,\ldots ,n\}$
is a normal submonoid of
$\{0,1,\ldots ,n\}$
is a normal submonoid of
![]() $\mathbb {N}_{\max }$
for each
$\mathbb {N}_{\max }$
for each
![]() $n\geq 0$
. It is clearly closed under products, but also under inverses because
$n\geq 0$
. It is clearly closed under products, but also under inverses because
![]() $0$
is the only invertible element. Moreover, the reader may easily check that
$0$
is the only invertible element. Moreover, the reader may easily check that
Since the product of elements
![]() $\leq n$
is
$\leq n$
is
![]() $\leq n$
, it follows that
$\leq n$
, it follows that
![]() $\{0,1,\ldots ,n\}$
is also invariant.
$\{0,1,\ldots ,n\}$
is also invariant.
Example 2.12. Let
![]() $\mathbb {N}\boxtimes\mathbb {N}$
be the set
$\mathbb {N}\boxtimes\mathbb {N}$
be the set
![]() $\mathbb {N}\times \mathbb {N}$
equipped with the product given by
$\mathbb {N}\times \mathbb {N}$
equipped with the product given by
Here,
![]() $\mathbb {N}\boxtimes\mathbb {N}$
is a commutative monoid, called the bicyclic monoid, with
$\mathbb {N}\boxtimes\mathbb {N}$
is a commutative monoid, called the bicyclic monoid, with
![]() $(0,0)$
as identity element (it is isomorphic to the monoid with presentation
$(0,0)$
as identity element (it is isomorphic to the monoid with presentation
![]() $\langle a,b\,|\,ab=1\rangle $
; see [Reference Howie8, pages 31–32]). Then the diagonal
$\langle a,b\,|\,ab=1\rangle $
; see [Reference Howie8, pages 31–32]). Then the diagonal
![]() $\Delta =\{(n,n) : n\geq 0\}$
is a normal submonoid. Indeed, it is clearly closed under products. Moreover, the reader may easily check that
$\Delta =\{(n,n) : n\geq 0\}$
is a normal submonoid. Indeed, it is clearly closed under products. Moreover, the reader may easily check that
![]() $(m,n)(p,q)=(0,0)$
if and only if
$(m,n)(p,q)=(0,0)$
if and only if
![]() $m=q=0$
and
$m=q=0$
and
![]() $n=p$
, while
$n=p$
, while
![]() $(n,0)(0,n)=(n,n)$
. Hence,
$(n,0)(0,n)=(n,n)$
. Hence,
![]() $(0,0)$
is the only invertible element, from which it follows that
$(0,0)$
is the only invertible element, from which it follows that
![]() $\Delta $
is also closed under inverses and hence, a groupal submonoid. To prove it is invariant, notice that
$\Delta $
is also closed under inverses and hence, a groupal submonoid. To prove it is invariant, notice that
so that
![]() $(k,l)(n,n)(r,s)\in \Delta $
if and only if
$(k,l)(n,n)(r,s)\in \Delta $
if and only if
![]() $k-l=s-r$
, independently of n. Hence,
$k-l=s-r$
, independently of n. Hence,
and indeed,
![]() $\Delta $
contains all its generalized conjugates. Notice that, as a monoid,
$\Delta $
contains all its generalized conjugates. Notice that, as a monoid,
![]() $\Delta $
is isomorphic to the monoid in Example 2.11 and hence,
$\Delta $
is isomorphic to the monoid in Example 2.11 and hence,
![]() $S_n:=\{(0,0),(1,1),\ldots ,(n,n)\}$
is a normal submonoid of
$S_n:=\{(0,0),(1,1),\ldots ,(n,n)\}$
is a normal submonoid of
![]() $\Delta $
for each
$\Delta $
for each
![]() $n\geq 0$
. However,
$n\geq 0$
. However,
![]() $S_n$
for
$S_n$
for
![]() $n\geq 2$
is not invariant as a groupal submonoid of
$n\geq 2$
is not invariant as a groupal submonoid of
![]() $\mathbb {N}\boxtimes\mathbb {N}$
. Thus,
$\mathbb {N}\boxtimes\mathbb {N}$
. Thus,
![]() $((n-1,1),(2,n))\in X_{S_n}$
because
$((n-1,1),(2,n))\in X_{S_n}$
because
![]() $(n-1,1)(2,n)=(n,n)$
but for
$(n-1,1)(2,n)=(n,n)$
but for
![]() $n>2$
, we have
$n>2$
, we have
![]() $(n-1,1)(n,n)(2,n)=(2n-2,2n-2)\notin S_n$
.
$(n-1,1)(n,n)(2,n)=(2n-2,2n-2)\notin S_n$
.
2.2 Normal closure
As for groups, given any subset A of a generic monoid M, by the normal closure of A (in M), we mean the smallest normal submonoid of M containing A. It is denoted by
![]() $\mathrm {ncl}_M(A)$
, or just
$\mathrm {ncl}_M(A)$
, or just
![]() $\mathrm {ncl}(A)$
if no confusion arises, and by
$\mathrm {ncl}(A)$
if no confusion arises, and by
![]() $\mathrm {ncl}_M(x_1,\ldots ,x_n)$
in the finite subset case
$\mathrm {ncl}_M(x_1,\ldots ,x_n)$
in the finite subset case
![]() $A=\{x_1,\ldots ,x_n\}$
.
$A=\{x_1,\ldots ,x_n\}$
.
The following result implies that
![]() $\mathrm {ncl}_M(A)$
is given as usual, that is, by the intersection of all normal submonoids of M containing A.
$\mathrm {ncl}_M(A)$
is given as usual, that is, by the intersection of all normal submonoids of M containing A.
Proposition 2.13. The intersection of normal submonoids of M is a normal submonoid of M.
Proof. Let
![]() $\{S_\lambda \}_{\lambda \in \Lambda }$
be a family of normal submonoids of M, and let
$\{S_\lambda \}_{\lambda \in \Lambda }$
be a family of normal submonoids of M, and let
Clearly, S is a groupal submonoid. Moreover, since
![]() $S\subseteq S_\lambda $
, we have
$S\subseteq S_\lambda $
, we have
![]() $X_{S}\subseteq X_{S_\lambda }$
for each
$X_{S}\subseteq X_{S_\lambda }$
for each
![]() $\lambda \in \Lambda $
. Thus, for each
$\lambda \in \Lambda $
. Thus, for each
![]() $(x,y)\in X_{S}$
,
$(x,y)\in X_{S}$
,
because each
![]() $S_\lambda $
is invariant. Hence,
$S_\lambda $
is invariant. Hence,
![]() $xSy\subseteq S$
, that is, S is also invariant.
$xSy\subseteq S$
, that is, S is also invariant.
Corollary 2.14. For every subset
![]() $A\subseteq M$
,
$A\subseteq M$
,
 $$ \begin{align*} \mathrm{ncl}_M(A)=\bigcap_{S\in\mathsf{NorSub}_A(M)}S \end{align*} $$
$$ \begin{align*} \mathrm{ncl}_M(A)=\bigcap_{S\in\mathsf{NorSub}_A(M)}S \end{align*} $$
with
![]() $\mathsf {NorSub}_A(M)$
the set of all normal submonoids of M containing A.
$\mathsf {NorSub}_A(M)$
the set of all normal submonoids of M containing A.
Furthermore, like any closure operator, the normal closure operator is idempotent, preserves inclusions, and it is such that for any subsets
![]() $A,B$
of M,
$A,B$
of M,
When M is a group G, the normal closure of A is the subgroup of G generated by the set of all conjugacy classes of elements in A. For a generic monoid, things are a little bit more sophisticated, and
![]() $\mathrm {ncl}_M(A)$
is built from A as follows. Let
$\mathrm {ncl}_M(A)$
is built from A as follows. Let
![]() $A_n$
for
$A_n$
for
![]() $n\geq 0$
be the groupal submonoids of M recursively defined by
$n\geq 0$
be the groupal submonoids of M recursively defined by
 $$ \begin{align} A_n&:=\bigg\langle\bigcup_{\tiny{(x,y)\in X_{A_{n-1}}}}xA_{n-1}y\bigg \rangle',\quad n\geq 1 \end{align} $$
$$ \begin{align} A_n&:=\bigg\langle\bigcup_{\tiny{(x,y)\in X_{A_{n-1}}}}xA_{n-1}y\bigg \rangle',\quad n\geq 1 \end{align} $$
with
![]() $\langle \rangle '$
the groupal submonoid generated by A, and
$\langle \rangle '$
the groupal submonoid generated by A, and
![]() $X_A$
the stability set of A for any subset
$X_A$
the stability set of A for any subset
![]() $A\subseteq M$
. Notice that
$A\subseteq M$
. Notice that
because
![]() $(1,1)\in X_{A}$
for each A. Consequently, we also have
$(1,1)\in X_{A}$
for each A. Consequently, we also have
Proposition 2.15. For every subset
![]() $A\subseteq M$
, the normal closure of A in M is
$A\subseteq M$
, the normal closure of A in M is
Proof. Every normal submonoid of M containing A must contain
![]() $\mathrm {ncl}_M(A)$
. Hence, it is enough to see that
$\mathrm {ncl}_M(A)$
. Hence, it is enough to see that
![]() $\mathrm {ncl}_M(A)$
is a normal submonoid. Let
$\mathrm {ncl}_M(A)$
is a normal submonoid. Let
![]() $z,z'\in \mathrm {ncl}_M(A)$
. Then
$z,z'\in \mathrm {ncl}_M(A)$
. Then
![]() $z\in A_n$
and
$z\in A_n$
and
![]() $z'\in A_{n'}$
for some
$z'\in A_{n'}$
for some
![]() $n,n'\geq 0$
. Since
$n,n'\geq 0$
. Since
![]() $A_n,A_{n'}\subseteq A_{\max \{n,n'\}}$
, it follows that
$A_n,A_{n'}\subseteq A_{\max \{n,n'\}}$
, it follows that
![]() $z,z'\in A_{\max \{n,n'\}}$
and hence,
$z,z'\in A_{\max \{n,n'\}}$
and hence,
![]() $zz'\in A_{\max \{n,n'\}}\subseteq \mathrm {ncl}_M(A)$
because
$zz'\in A_{\max \{n,n'\}}\subseteq \mathrm {ncl}_M(A)$
because
![]() $A_{\max \{n,n'\}}$
is a submonoid. Moreover, if
$A_{\max \{n,n'\}}$
is a submonoid. Moreover, if
![]() $z\in U(M)$
, we also have
$z\in U(M)$
, we also have
![]() $z^{-1}\in A_{\max \{n,n'\}}$
because it is a groupal submonoid. This proves that
$z^{-1}\in A_{\max \{n,n'\}}$
because it is a groupal submonoid. This proves that
![]() $\mathrm {ncl}_M(A)$
is a groupal submonoid of M. To prove that it is invariant, let us first observe that
$\mathrm {ncl}_M(A)$
is a groupal submonoid of M. To prove that it is invariant, let us first observe that
Indeed, since
![]() $A_n\subseteq \mathrm {ncl}_M(A)$
, we have
$A_n\subseteq \mathrm {ncl}_M(A)$
, we have
![]() $X_{A_n}\subseteq X_{\mathrm {ncl}_M(A)}$
for each
$X_{A_n}\subseteq X_{\mathrm {ncl}_M(A)}$
for each
![]() $n\geq 0$
and hence,
$n\geq 0$
and hence,
![]() $\bigcup _{n\geq 0}X_{A_n}\subseteq X_{\mathrm {ncl}_M(A)}$
. Conversely, let
$\bigcup _{n\geq 0}X_{A_n}\subseteq X_{\mathrm {ncl}_M(A)}$
. Conversely, let
![]() $(x,y)\in X_{\mathrm {ncl}_M(A)}$
. This means that there exist
$(x,y)\in X_{\mathrm {ncl}_M(A)}$
. This means that there exist
![]() $t^*_1,t^*_2\in \mathrm {ncl}_M(A)$
such that
$t^*_1,t^*_2\in \mathrm {ncl}_M(A)$
such that
![]() $x t^*_1y=t^*_2$
and hence, some
$x t^*_1y=t^*_2$
and hence, some
![]() $n_1,n_2\geq 0$
such that
$n_1,n_2\geq 0$
such that
![]() $t^*_1\in A_{n_1}$
,
$t^*_1\in A_{n_1}$
,
![]() $t^*_2\in A_{n_2}$
, and
$t^*_2\in A_{n_2}$
, and
![]() $xt^*_1y=t^*_2$
. Since
$xt^*_1y=t^*_2$
. Since
![]() $A_{n_1},A_{n_2}\subseteq A_{\max \{n_1,n_2\}}$
, it follows that
$A_{n_1},A_{n_2}\subseteq A_{\max \{n_1,n_2\}}$
, it follows that
![]() $(x,y)\in A_{\max \{n_1,n_2\}}\subseteq \bigcup _{n\geq 0}X_{A_n}$
. Let now
$(x,y)\in A_{\max \{n_1,n_2\}}\subseteq \bigcup _{n\geq 0}X_{A_n}$
. Let now
![]() $(x,y)\in X_{\mathrm {ncl}_M(A)}$
, and let us prove that
$(x,y)\in X_{\mathrm {ncl}_M(A)}$
, and let us prove that
![]() $x\mathrm {ncl}_M(A)y\subseteq \mathrm {ncl}_M(A)$
. Indeed, it follows from Equation (2-5) that
$x\mathrm {ncl}_M(A)y\subseteq \mathrm {ncl}_M(A)$
. Indeed, it follows from Equation (2-5) that
![]() $(x,y)\in X_{A_{n_0}}$
for some
$(x,y)\in X_{A_{n_0}}$
for some
![]() $n_0\geq 0$
and hence,
$n_0\geq 0$
and hence,
![]() $(x,y)\in X_{A_n}$
for each
$(x,y)\in X_{A_n}$
for each
![]() $n\geq n_0$
. Then for any element
$n\geq n_0$
. Then for any element
![]() $t^*\in \mathrm {ncl}_M(A)$
, we have
$t^*\in \mathrm {ncl}_M(A)$
, we have
![]() $t^*\in A_{m_0}$
for some
$t^*\in A_{m_0}$
for some
![]() $m_0\geq 0$
and hence,
$m_0\geq 0$
and hence,
![]() $t^*\in A_m$
for each
$t^*\in A_m$
for each
![]() $m\geq m_0$
. If
$m\geq m_0$
. If
![]() $m_0\leq n_0$
, we have
$m_0\leq n_0$
, we have
![]() $t^*\in A_{n_0}$
and
$t^*\in A_{n_0}$
and
![]() $(x,y)\in X_{A_{n_0}}$
, from which it follows that
$(x,y)\in X_{A_{n_0}}$
, from which it follows that
![]() $xt^*y\in A_{n_0+1}\subseteq \mathrm {ncl}_M(A)$
. Similarly, if
$xt^*y\in A_{n_0+1}\subseteq \mathrm {ncl}_M(A)$
. Similarly, if
![]() $m_0>n_0$
, we have
$m_0>n_0$
, we have
![]() $t^*\in A_{m_0}$
and
$t^*\in A_{m_0}$
and
![]() $(x,y)\in X_{A_{m_0}}$
, from which it follows that
$(x,y)\in X_{A_{m_0}}$
, from which it follows that
![]() $xt^*y\in A_{m_0+1}\subseteq \mathrm {ncl}_M(A)$
.
$xt^*y\in A_{m_0+1}\subseteq \mathrm {ncl}_M(A)$
.
Notice that for a commutative monoid
![]() $M=(M,+,0)$
, the generating set of
$M=(M,+,0)$
, the generating set of
![]() $A_n$
for
$A_n$
for
![]() $n\geq 1$
can also be described by
$n\geq 1$
can also be described by
 $$ \begin{align*} \bigcup_{(x,y)\in X_{A_{n-1}}}(x+A_{n-1}+y)=\bigcup_{z\in LX_{A_{n-1}}}(z+A_{n-1}), \end{align*} $$
$$ \begin{align*} \bigcup_{(x,y)\in X_{A_{n-1}}}(x+A_{n-1}+y)=\bigcup_{z\in LX_{A_{n-1}}}(z+A_{n-1}), \end{align*} $$
where
![]() $LX_A$
for any subset
$LX_A$
for any subset
![]() $A\subseteq M$
stands for the (left) one-sided stability set of A, that is,
$A\subseteq M$
stands for the (left) one-sided stability set of A, that is,
Thus, if
![]() $z\in LX_A$
, then
$z\in LX_A$
, then
![]() $(z,0)\in X_A$
and conversely, if
$(z,0)\in X_A$
and conversely, if
![]() $(x,y)\in X_A$
, then
$(x,y)\in X_A$
, then
![]() $x+y\in LX_A$
. Hence, the set on either side is indeed a subset of the set on the other side.
$x+y\in LX_A$
. Hence, the set on either side is indeed a subset of the set on the other side.
Example 2.16. For every
![]() $n_1,\ldots ,n_k\geq 0$
with
$n_1,\ldots ,n_k\geq 0$
with
![]() $k\geq 1$
, the normal closure of
$k\geq 1$
, the normal closure of
![]() $\{n_1,\ldots ,n_k\}$
is
$\{n_1,\ldots ,n_k\}$
is
 $$ \begin{align*} \mathrm{ncl}_{\mathbb{N}_+}(n_1,\ldots,n_k)= \begin{cases} \langle n_1\rangle & \mbox{if } k=1, \\ \langle\gcd(n_1,\ldots,n_k)\rangle & \mbox{if } k\geq 2. \end{cases} \end{align*} $$
$$ \begin{align*} \mathrm{ncl}_{\mathbb{N}_+}(n_1,\ldots,n_k)= \begin{cases} \langle n_1\rangle & \mbox{if } k=1, \\ \langle\gcd(n_1,\ldots,n_k)\rangle & \mbox{if } k\geq 2. \end{cases} \end{align*} $$
Let us first prove the case
![]() $k=1$
. We have to see that
$k=1$
. We have to see that
for each
![]() $n\geq 0$
. Since
$n\geq 0$
. Since
![]() $U(M)=\{0\}$
, we have
$U(M)=\{0\}$
, we have
![]() $\{n\}_0=\langle n\rangle '=\langle n\rangle $
. Now
$\{n\}_0=\langle n\rangle '=\langle n\rangle $
. Now
![]() $LX_{\langle n\rangle }$
consists of the positive integers
$LX_{\langle n\rangle }$
consists of the positive integers
![]() $p\in \mathbb {N}$
such that
$p\in \mathbb {N}$
such that
![]() $p+\langle n\rangle $
contains some multiple of n and consequently, of those
$p+\langle n\rangle $
contains some multiple of n and consequently, of those
![]() $p\geq 0$
such that
$p\geq 0$
such that
![]() $p\in \langle n\rangle $
. Hence, for each
$p\in \langle n\rangle $
. Hence, for each
![]() $p\in LX_{\langle n\rangle }$
, we have
$p\in LX_{\langle n\rangle }$
, we have
![]() $p+\langle n\rangle \subseteq \langle n\rangle $
and
$p+\langle n\rangle \subseteq \langle n\rangle $
and
![]() $\{n\}_1=\{n\}_0$
, from which the claim readily follows. Let us now prove the cases
$\{n\}_1=\{n\}_0$
, from which the claim readily follows. Let us now prove the cases
![]() $k\geq 2$
by induction on k. Let
$k\geq 2$
by induction on k. Let
![]() $k=2$
. If
$k=2$
. If
![]() $n_1=n_2$
, the result follows from Equation (2-6). If
$n_1=n_2$
, the result follows from Equation (2-6). If
![]() $n_1\neq n_2$
,
$n_1\neq n_2$
,
Now, assuming that
![]() $n_1<n_2$
, we have
$n_1<n_2$
, we have
![]() $n_2=qn_1+r_1$
for some
$n_2=qn_1+r_1$
for some
![]() $q\geq 1$
and
$q\geq 1$
and
![]() $0<r_1<m$
. Hence,
$0<r_1<m$
. Hence,
![]() $r_1\in LX_{\langle n_1,n_2\rangle }$
. Thus,
$r_1\in LX_{\langle n_1,n_2\rangle }$
. Thus,
By the same argument applied to the subset
![]() $\{r_1,n_1\}$
, it follows that
$\{r_1,n_1\}$
, it follows that
where
![]() $r_2$
is the remainder of the euclidean division of
$r_2$
is the remainder of the euclidean division of
![]() $n_1$
by
$n_1$
by
![]() $r_1$
. In particular,
$r_1$
. In particular,
![]() $r_2\in \{n_1,n_2\}_2$
. After a finite number
$r_2\in \{n_1,n_2\}_2$
. After a finite number
![]() $p\geq 1$
of iterations, we find that
$p\geq 1$
of iterations, we find that
and hence,
![]() $\langle \gcd (n_1,n_2)\rangle \subseteq \mathrm {ncl}_{\mathbb {N}_+}(n_1,n_2)$
. The equality follows because
$\langle \gcd (n_1,n_2)\rangle \subseteq \mathrm {ncl}_{\mathbb {N}_+}(n_1,n_2)$
. The equality follows because
![]() $\langle \gcd (n_1,n_2)\rangle $
is already a normal submonoid containing
$\langle \gcd (n_1,n_2)\rangle $
is already a normal submonoid containing
![]() $n_1,n_2$
. Let now
$n_1,n_2$
. Let now
![]() $k>2$
, and let us assume that
$k>2$
, and let us assume that
![]() $\mathrm {ncl}_{\mathbb {N}_+}(n_1,\ldots ,n_{k-1})=\langle \gcd (n_1,\ldots ,n_{k-1})\rangle $
for every
$\mathrm {ncl}_{\mathbb {N}_+}(n_1,\ldots ,n_{k-1})=\langle \gcd (n_1,\ldots ,n_{k-1})\rangle $
for every
![]() $n_1,\ldots ,n_{k-1}\geq 0$
. Then,
$n_1,\ldots ,n_{k-1}\geq 0$
. Then,
 $$ \begin{align*} \mathrm{ncl}_{\mathbb{N}_+}(n_1,\ldots,n_k)&=\mathrm{ncl}_{\mathbb{N}_+}(\{n_1,\ldots,n_{k-1}\}\cup\{n_k\}) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\mathrm{ncl}_{\mathbb{N}_+}(n_1,\ldots,n_{k-1})\cup\mathrm{ncl}_{\mathbb{N}_+}(n_k)) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\langle\gcd(n_1,\ldots,n_{k-1})\rangle\cup\langle n_k\rangle) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\mathrm{ncl}_{\mathbb{N}_+}(\gcd(n_1,\ldots,n_{k-1}))\cup\mathrm{ncl}_{\mathbb{N}_+}(n_k)) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\gcd(n_1,\ldots,n_{k-1}),n_k) \\ &=\langle\gcd(\gcd(n_1,\ldots,n_{k-1}),n_k)\rangle \\ &=\langle\gcd(n_1,\ldots,n_k)\rangle. \end{align*} $$
$$ \begin{align*} \mathrm{ncl}_{\mathbb{N}_+}(n_1,\ldots,n_k)&=\mathrm{ncl}_{\mathbb{N}_+}(\{n_1,\ldots,n_{k-1}\}\cup\{n_k\}) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\mathrm{ncl}_{\mathbb{N}_+}(n_1,\ldots,n_{k-1})\cup\mathrm{ncl}_{\mathbb{N}_+}(n_k)) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\langle\gcd(n_1,\ldots,n_{k-1})\rangle\cup\langle n_k\rangle) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\mathrm{ncl}_{\mathbb{N}_+}(\gcd(n_1,\ldots,n_{k-1}))\cup\mathrm{ncl}_{\mathbb{N}_+}(n_k)) \\ &=\mathrm{ncl}_{\mathbb{N}_+}(\gcd(n_1,\ldots,n_{k-1}),n_k) \\ &=\langle\gcd(\gcd(n_1,\ldots,n_{k-1}),n_k)\rangle \\ &=\langle\gcd(n_1,\ldots,n_k)\rangle. \end{align*} $$
Example 2.17. For each
![]() $n\geq 0$
, the normal closure of
$n\geq 0$
, the normal closure of
![]() $\{n\}$
in
$\{n\}$
in
![]() $\mathbb {N}_{\max }$
(see Example 2.11) is given by
$\mathbb {N}_{\max }$
(see Example 2.11) is given by
Indeed, since
![]() $U(\mathbb {N}_{\max })=\{0\}$
,
$U(\mathbb {N}_{\max })=\{0\}$
,
Now it is easy to check that
![]() $LX_{\{0,n\}}=\{0,1,\ldots ,n\}$
and hence,
$LX_{\{0,n\}}=\{0,1,\ldots ,n\}$
and hence,
Then Equation (2-7) follows because this is already a normal submonoid. More generally, an easy induction on
![]() $k\geq 1$
shows that
$k\geq 1$
shows that
The details are left to the reader.
2.3 Normal and normally simple monoids
As a (groupal) submonoid of M, the group of units
![]() $U(M)$
is invariant if (and only if) for every pair
$U(M)$
is invariant if (and only if) for every pair
![]() $(x,y)\in M\times M$
for which there exists some
$(x,y)\in M\times M$
for which there exists some
![]() $u\in U(M)$
such that
$u\in U(M)$
such that
![]() $xuy\in U(M)$
, we have
$xuy\in U(M)$
, we have
![]() $xu'y\in U(M)$
for each
$xu'y\in U(M)$
for each
![]() $u'\in U(M)$
. There seems to be no reason why this should be true for a generic monoid M. This suggests introducing the following definition.
$u'\in U(M)$
. There seems to be no reason why this should be true for a generic monoid M. This suggests introducing the following definition.
Definition 2.18. A monoid M is called normal when its group of units
![]() $U(M)$
is a normal submonoid.
$U(M)$
is a normal submonoid.
Clearly, every group, finite or not, is a normal monoid, as is every monoid whose group of units is trivial, such as any free monoid, and the bicyclic monoid
![]() $\mathbb {N}\boxtimes\mathbb {N}$
of Example 2.12. Many more examples are provided by the next result.
$\mathbb {N}\boxtimes\mathbb {N}$
of Example 2.12. Many more examples are provided by the next result.
Proposition 2.19. Let M be a monoid. Then M is normal in any of the following two cases:
-
(i) M is finite;
-
(ii) M is commutative.
Proof. (i) Let M be a finite monoid that is not a group, that is, such that
![]() $M\setminus U(M)\neq \emptyset $
. Then the stability set of
$M\setminus U(M)\neq \emptyset $
. Then the stability set of
![]() $U(M)$
is
$U(M)$
is
from which the statement follows readily. The inclusion
![]() $U(M)\times U(M)\subseteq X_{U(M)}$
is obvious. Regarding the reverse inclusion, it is ultimately a consequence of the so-called stability property of finite monoids, according to which for a finite monoid M, and for every
$U(M)\times U(M)\subseteq X_{U(M)}$
is obvious. Regarding the reverse inclusion, it is ultimately a consequence of the so-called stability property of finite monoids, according to which for a finite monoid M, and for every
![]() $x,y\in M$
, the two following equivalences hold:
$x,y\in M$
, the two following equivalences hold:
-
(1)
 $MxM=MxyM$
$MxM=MxyM$
 $\Longleftrightarrow xM = xyM$
;
$\Longleftrightarrow xM = xyM$
; -
(2)
 $MxM=MyxM$
$MxM=MyxM$
 $\Longleftrightarrow Mx = Myx$
.
$\Longleftrightarrow Mx = Myx$
.
Using either of these equivalences, it is not difficult to see that
and that its complement
![]() $M\setminus U(M)$
, nonempty by hypothesis, is a (two-sided) ideal of M; see, for example, [Reference Steinberg12, Section 1.3] for the details. Now, if
$M\setminus U(M)$
, nonempty by hypothesis, is a (two-sided) ideal of M; see, for example, [Reference Steinberg12, Section 1.3] for the details. Now, if
![]() $M\setminus U(M)$
is an ideal and for some
$M\setminus U(M)$
is an ideal and for some
![]() $x,y\in M$
, there exists some
$x,y\in M$
, there exists some
![]() $u\in U(M)$
such that
$u\in U(M)$
such that
![]() $xuy\in U(M)$
, we necessarily have
$xuy\in U(M)$
, we necessarily have
![]() $x,y\in U(M)$
. Hence,
$x,y\in U(M)$
. Hence,
![]() $X_{U(M)}=U(M)\times U(M)$
.
$X_{U(M)}=U(M)\times U(M)$
.
(ii) If M is commutative and
![]() $xuy\in U(M)$
for some
$xuy\in U(M)$
for some
![]() $u\in U(M)$
, it follows that
$u\in U(M)$
, it follows that
![]() $xy\in U(M)$
and hence,
$xy\in U(M)$
and hence,
![]() $xu'y=xyu'\in U(M)$
for each
$xu'y=xyu'\in U(M)$
for each
![]() $u'\in U(M)$
.
$u'\in U(M)$
.
Proposition 2.20. Let M be a normal monoid. Then every normal subgroup of
![]() $U(M)$
is a normal submonoid of M.
$U(M)$
is a normal submonoid of M.
Proof. Every subgroup H of
![]() $U(M)$
is trivially a groupal submonoid of M. Let us assume that H is a normal subgroup of
$U(M)$
is trivially a groupal submonoid of M. Let us assume that H is a normal subgroup of
![]() $U(M)$
and that for some
$U(M)$
and that for some
![]() $x,y\in M$
, we have
$x,y\in M$
, we have
![]() $(xHy)\cap H\neq \emptyset $
. Since
$(xHy)\cap H\neq \emptyset $
. Since
![]() $H\subseteq U(M)$
, we also have
$H\subseteq U(M)$
, we also have
![]() $(xU(M)y)\cap U(M)\neq \emptyset $
and hence,
$(xU(M)y)\cap U(M)\neq \emptyset $
and hence,
![]() $xU(M)y\subseteq U(M)$
because
$xU(M)y\subseteq U(M)$
because
![]() $U(M)$
is a normal submonoid of M. Then for every
$U(M)$
is a normal submonoid of M. Then for every
![]() $h\in H$
, we have
$h\in H$
, we have
![]() $xhy\in U(M)$
.
$xhy\in U(M)$
.
In general, a normal monoid M may have normal submonoids other than itself, and the normal subgroups of
![]() $U(M)$
. For instance, this is so for the monoid
$U(M)$
. For instance, this is so for the monoid
![]() $\mathbb {N}_+$
(compare with Proposition 2.9), and for the monoids in Examples 2.11 and 2.12.
$\mathbb {N}_+$
(compare with Proposition 2.9), and for the monoids in Examples 2.11 and 2.12.
Definition 2.21. A normal monoid M is called normally simple if its only normal submonoids are M and the normal subgroups of
![]() $U(M)$
.
$U(M)$
.
Clearly, every group is a normally simple monoid. An important family of normally simple noncommutative monoids that are not groups is the family of full transformation monoids
![]() $T_n:=End(\mathbf {n})$
for each
$T_n:=End(\mathbf {n})$
for each
![]() $n\geq 1$
, where
$n\geq 1$
, where
![]() $\mathbf {n}:=\{1,\ldots ,n\}$
.
$\mathbf {n}:=\{1,\ldots ,n\}$
.
Proposition 2.22.
![]() $T_n$
is normally simple for each
$T_n$
is normally simple for each
![]() $n\geq 1$
.
$n\geq 1$
.
Proof. Here,
![]() $T_n$
is a normal monoid because it is finite. To prove that it is normally simple it is enough to see that for each
$T_n$
is a normal monoid because it is finite. To prove that it is normally simple it is enough to see that for each
![]() $f\in T_n$
, the normal closure of
$f\in T_n$
, the normal closure of
![]() $\{f\}$
in
$\{f\}$
in
![]() $T_n$
is given by
$T_n$
is given by
 $$ \begin{align} \mathrm{ncl}_{T_n}(f)= \begin{cases} \mathrm{ncl}_{S_n}(f) & \mbox{if } f\in S_n, \\ T_n & \mbox{if } f\notin S_n, \end{cases} \end{align} $$
$$ \begin{align} \mathrm{ncl}_{T_n}(f)= \begin{cases} \mathrm{ncl}_{S_n}(f) & \mbox{if } f\in S_n, \\ T_n & \mbox{if } f\notin S_n, \end{cases} \end{align} $$
where
![]() $\mathrm {ncl}_{S_n}(f)$
stands for the normal closure of
$\mathrm {ncl}_{S_n}(f)$
stands for the normal closure of
![]() $\{f\}$
in the symmetric group
$\{f\}$
in the symmetric group
![]() $S_n$
. Indeed, let this be true and let S be a normal submonoid of
$S_n$
. Indeed, let this be true and let S be a normal submonoid of
![]() $T_n$
. If
$T_n$
. If
![]() $S\setminus S_n\neq \emptyset $
and
$S\setminus S_n\neq \emptyset $
and
![]() $f\in S\cap S_n$
, it follows from Equation (2-8) that
$f\in S\cap S_n$
, it follows from Equation (2-8) that
![]() $T_n=\mathrm {ncl}_{T_n}(f)\subseteq S$
and hence,
$T_n=\mathrm {ncl}_{T_n}(f)\subseteq S$
and hence,
![]() $S=T_n$
. Otherwise, we have
$S=T_n$
. Otherwise, we have
![]() $S\subseteq S_n$
and, being a normal submonoid of
$S\subseteq S_n$
and, being a normal submonoid of
![]() $T_n$
, S is also a normal submonoid of
$T_n$
, S is also a normal submonoid of
![]() $S_n$
and hence, a normal subgroup of
$S_n$
and hence, a normal subgroup of
![]() $S_n$
.
$S_n$
.
Let us prove Equation (2-8). We need to compute the sequence of groupal submonoids
![]() $\{f\}_0,\{f\}_1,\ldots .$
Let us first consider the case where f is a permutation. By definition,
$\{f\}_0,\{f\}_1,\ldots .$
Let us first consider the case where f is a permutation. By definition,
Then the stability set of
![]() $\{f\}_0$
consists of all pairs
$\{f\}_0$
consists of all pairs
![]() $(g,h)\in T_n\times T_n$
such that
$(g,h)\in T_n\times T_n$
such that
![]() $gf^ph=f^q$
for some
$gf^ph=f^q$
for some
![]() $p,q\in \mathbb {Z}$
. Since f is a bijection, h must be injective and g surjective. Being endomorphisms of
$p,q\in \mathbb {Z}$
. Since f is a bijection, h must be injective and g surjective. Being endomorphisms of
![]() $\mathbf {n}$
, it follows that
$\mathbf {n}$
, it follows that
![]() $g,h\in S_n$
. Hence, we can take as g any permutation in
$g,h\in S_n$
. Hence, we can take as g any permutation in
![]() $S_n$
, and
$S_n$
, and
![]() $h=f^qg^{-1}f^{-p}$
, that is,
$h=f^qg^{-1}f^{-p}$
, that is,
In particular,
![]() $(\tau ,\tau ^{-1})\in X_{\{f\}_0}$
for each
$(\tau ,\tau ^{-1})\in X_{\{f\}_0}$
for each
![]() $\tau \in S_n$
. Thus,
$\tau \in S_n$
. Thus,
 $$ \begin{align*} \mathrm{ncl}_{T_n}(f)\supseteq\{f\}_1=\bigg\langle\bigcup_{(g,h)\in X_{\{f\}_0}}g\{f\}_0h\ \bigg\rangle'\supseteq\bigg\langle \bigcup_{\tau\in S_n}\tau\{f\}_0\tau^{-1}\,\bigg\rangle'\supseteq\mathrm{ncl}_{S_n}(f). \end{align*} $$
$$ \begin{align*} \mathrm{ncl}_{T_n}(f)\supseteq\{f\}_1=\bigg\langle\bigcup_{(g,h)\in X_{\{f\}_0}}g\{f\}_0h\ \bigg\rangle'\supseteq\bigg\langle \bigcup_{\tau\in S_n}\tau\{f\}_0\tau^{-1}\,\bigg\rangle'\supseteq\mathrm{ncl}_{S_n}(f). \end{align*} $$
However,
![]() $\mathrm {ncl}_{S_n}(f)$
is already a normal submonoid of
$\mathrm {ncl}_{S_n}(f)$
is already a normal submonoid of
![]() $T_n$
containing f because of Proposition 2.20. Therefore,
$T_n$
containing f because of Proposition 2.20. Therefore,
![]() $\mathrm {ncl}_{T_n}(f)=\mathrm {ncl}_{S_n}(f)$
when f is invertible.
$\mathrm {ncl}_{T_n}(f)=\mathrm {ncl}_{S_n}(f)$
when f is invertible.
Let now f be a noninvertible endomorphism. To prove that
![]() $\mathrm {ncl}(f)=T_n$
, we proceed by induction on the rank
$\mathrm {ncl}(f)=T_n$
, we proceed by induction on the rank
![]() $k<n$
of f. If
$k<n$
of f. If
![]() $k=1$
, there exists
$k=1$
, there exists
![]() $i\in \mathbf {n}$
such that
$i\in \mathbf {n}$
such that
![]() $f=c_i$
, the constant function mapping all of
$f=c_i$
, the constant function mapping all of
![]() $\mathbf {n}$
to i. Now,
$\mathbf {n}$
to i. Now,
and for every
![]() $h\in T_n$
, we have
$h\in T_n$
, we have
![]() $c_ih=c_i$
, that is,
$c_ih=c_i$
, that is,
![]() $(\mathrm {id}_{\mathbf {n}},h)\in X_{\{c_i\}_0}$
. It follows that for every
$(\mathrm {id}_{\mathbf {n}},h)\in X_{\{c_i\}_0}$
. It follows that for every
![]() $h\in T_n$
,
$h\in T_n$
,
that is,
![]() $\mathrm {ncl}_{T_n}(f)=T_n$
. Let us now assume that
$\mathrm {ncl}_{T_n}(f)=T_n$
. Let us now assume that
![]() $ncl_{T_n}(\phi )=T_n$
for every endomorphism
$ncl_{T_n}(\phi )=T_n$
for every endomorphism
![]() $\phi \in T_n$
of rank
$\phi \in T_n$
of rank
![]() $l\in \{1,\ldots ,k-1\}$
, with
$l\in \{1,\ldots ,k-1\}$
, with
![]() $1<k<n$
. Since f is not invertible,
$1<k<n$
. Since f is not invertible,
Let
![]() $\mathrm {Im}f=\{i_1<i_2<\cdots <i_k\}\subset \mathbf {n}$
and
$\mathrm {Im}f=\{i_1<i_2<\cdots <i_k\}\subset \mathbf {n}$
and
![]() $\{A_1,\ldots ,A_k\}$
the partition of
$\{A_1,\ldots ,A_k\}$
the partition of
![]() $\mathbf {n}$
such that
$\mathbf {n}$
such that
![]() $f^{-1}(i_j)=A_j$
. Thus,
$f^{-1}(i_j)=A_j$
. Thus,
![]() $f=\varepsilon \eta $
, with
$f=\varepsilon \eta $
, with
![]() $\eta :\mathbf {n}\to \{i_1,\ldots ,i_k\}$
given by
$\eta :\mathbf {n}\to \{i_1,\ldots ,i_k\}$
given by
![]() $A_j\mapsto i_j$
, and
$A_j\mapsto i_j$
, and
![]() $\varepsilon :\{i_1,\ldots ,i_k\}\to \mathbf {n}$
the canonical inclusion. Then the powers of f can be described in terms of the map
$\varepsilon :\{i_1,\ldots ,i_k\}\to \mathbf {n}$
the canonical inclusion. Then the powers of f can be described in terms of the map
![]() $\alpha :\{i_1,\ldots ,i_k\}\to \{i_1,\ldots ,i_k\}$
defined by
$\alpha :\{i_1,\ldots ,i_k\}\to \{i_1,\ldots ,i_k\}$
defined by
where
![]() $j'$
is the unique element in
$j'$
is the unique element in
![]() $\{1,\ldots ,k\}$
such that
$\{1,\ldots ,k\}$
such that
![]() $i_j\in A_{j'}$
. Thus,
$i_j\in A_{j'}$
. Thus,
![]() $f^2$
is given by
$f^2$
is given by
![]() $A_j\overset {f}{\mapsto } i_j\overset {f}{\mapsto } i_{j'}$
, that is, we have
$A_j\overset {f}{\mapsto } i_j\overset {f}{\mapsto } i_{j'}$
, that is, we have
![]() $f^2=\varepsilon \alpha \eta $
. More generally, for each
$f^2=\varepsilon \alpha \eta $
. More generally, for each
![]() $p\geq 1$
,
$p\geq 1$
,
The map
![]() $\alpha $
can be bijective or not. If it is not bijective, it follows that the powers of f all have rank less than k. However, if
$\alpha $
can be bijective or not. If it is not bijective, it follows that the powers of f all have rank less than k. However, if
![]() $\{f\}_0$
contains a map
$\{f\}_0$
contains a map
![]() $\phi $
of rank
$\phi $
of rank
![]() $l<k$
, it follows by the induction hypothesis that
$l<k$
, it follows by the induction hypothesis that
![]() $T_n=\mathrm {ncl}_{T_n}(\phi )$
, and hence
$T_n=\mathrm {ncl}_{T_n}(\phi )$
, and hence
![]() $\mathrm {ncl}_{T_n}(f)=T_n$
because
$\mathrm {ncl}_{T_n}(f)=T_n$
because
![]() $\mathrm {ncl}_{T_n}(\phi )\subseteq \mathrm {ncl}_{T_n}(f)$
. It remains to prove that the same is true when
$\mathrm {ncl}_{T_n}(\phi )\subseteq \mathrm {ncl}_{T_n}(f)$
. It remains to prove that the same is true when
![]() $\alpha $
is not bijective. In this case, all powers of f are of rank k. However, we claim that when
$\alpha $
is not bijective. In this case, all powers of f are of rank k. However, we claim that when
![]() $\alpha $
is not bijective,
$\alpha $
is not bijective,
![]() $\{f\}_1$
contains maps of rank less than k, so that the same argument can be applied. Indeed, since f is not a bijection, there is some
$\{f\}_1$
contains maps of rank less than k, so that the same argument can be applied. Indeed, since f is not a bijection, there is some
![]() $j\in \{1,\ldots ,k\}$
such that
$j\in \{1,\ldots ,k\}$
such that
![]() $A_j$
contains more than one element. Without loss of generality, let us assume that
$A_j$
contains more than one element. Without loss of generality, let us assume that
![]() $|A_1|>2$
. Moreover, since
$|A_1|>2$
. Moreover, since
![]() $\alpha $
is a bijection, each
$\alpha $
is a bijection, each
![]() $i_j$
belongs to a different
$i_j$
belongs to a different
![]() $A_{j'}$
and hence, there is some
$A_{j'}$
and hence, there is some
![]() $a_1\in A_1$
such that
$a_1\in A_1$
such that
![]() $a_1\notin \{i_1,\ldots ,i_k\}$
. Then let us consider the pair
$a_1\notin \{i_1,\ldots ,i_k\}$
. Then let us consider the pair
![]() $(g,h)\in T_n\times T_n$
given as follows:
$(g,h)\in T_n\times T_n$
given as follows:
-
(i) h maps all of
 $A_1$
to
$A_1$
to
 $a_1$
, and each
$a_1$
, and each
 $A_j$
for
$A_j$
for
 $j\in \{2,\ldots ,k\}$
to any
$j\in \{2,\ldots ,k\}$
to any
 $a_j\in A_j$
;
$a_j\in A_j$
; -
(ii) g acts as the identity on
 $\{i_1,\ldots ,i_k\}$
, and collapses
$\{i_1,\ldots ,i_k\}$
, and collapses
 $\mathbf {n}\setminus \{i_1,\ldots ,i_k\}$
to
$\mathbf {n}\setminus \{i_1,\ldots ,i_k\}$
to
 $i_2$
(in particular, we have
$i_2$
(in particular, we have
 $g(a_1)=i_2$
).
$g(a_1)=i_2$
).
Then we have
![]() $gfh=f$
, that is,
$gfh=f$
, that is,
![]() $(g,h)\in X_{\{f\}_0}$
and hence,
$(g,h)\in X_{\{f\}_0}$
and hence,
![]() $gh\in \{f\}_1$
. However,
$gh\in \{f\}_1$
. However,
![]() $gh$
is of rank at most
$gh$
is of rank at most
![]() $k-1$
because even if
$k-1$
because even if
![]() $\{a_2,\ldots ,a_k\}=\{i_2,\ldots ,i_k\}$
, we have that
$\{a_2,\ldots ,a_k\}=\{i_2,\ldots ,i_k\}$
, we have that
![]() $a_1$
is also mapped to
$a_1$
is also mapped to
![]() $i_2$
.
$i_2$
.
2.4 Lattice of normal submonoids and modularity
As the set of normal subgroups of a group, the set
![]() $\mathsf {NorSub}(M)$
of normal submonoids of a monoid M is a complete lattice when ordered by inclusion, with meets and joins respectively given by
$\mathsf {NorSub}(M)$
of normal submonoids of a monoid M is a complete lattice when ordered by inclusion, with meets and joins respectively given by
 $$ \begin{align*} \bigwedge_{i\in I}S_i&=\bigcap_{i\in I}S_i, \\ \bigvee_{i\in I}S_i&=\mathrm{ncl}_M\bigg(\bigcup_{i\in I}S_i\bigg) \end{align*} $$
$$ \begin{align*} \bigwedge_{i\in I}S_i&=\bigcap_{i\in I}S_i, \\ \bigvee_{i\in I}S_i&=\mathrm{ncl}_M\bigg(\bigcup_{i\in I}S_i\bigg) \end{align*} $$
for every family of normal submonoids
![]() $\{S_i\}_{i\in I}$
. In general, computing this lattice for a given monoid M may be quite difficult, if possible at all, or the resulting lattice may be a complex one. In some cases, however, it is just a (finite or infinite) chain.
$\{S_i\}_{i\in I}$
. In general, computing this lattice for a given monoid M may be quite difficult, if possible at all, or the resulting lattice may be a complex one. In some cases, however, it is just a (finite or infinite) chain.
Example 2.23. Let us write
![]() $[n]:=\{0,1,\ldots ,n\}$
for each
$[n]:=\{0,1,\ldots ,n\}$
for each
![]() $n\geq 0$
. Then the lattice of normal submonoids of
$n\geq 0$
. Then the lattice of normal submonoids of
![]() $\mathbb {N}_{\max }$
is the infinite chain
$\mathbb {N}_{\max }$
is the infinite chain
Indeed, let S be a normal submonoid of
![]() $\mathbb {N}_{\max }$
. If S is a bounded set and n is its maximum, we have
$\mathbb {N}_{\max }$
. If S is a bounded set and n is its maximum, we have
![]() $S=[n]$
because
$S=[n]$
because
![]() $\mathrm {ncl}_{\mathbb {N}_{\max }}(n)=[n]$
(compare with Example 2.17). Otherwise, for each
$\mathrm {ncl}_{\mathbb {N}_{\max }}(n)=[n]$
(compare with Example 2.17). Otherwise, for each
![]() $k\geq 0$
, there is some element
$k\geq 0$
, there is some element
![]() $n\in S$
with
$n\in S$
with
![]() $n>k$
because S is not bounded. Therefore,
$n>k$
because S is not bounded. Therefore,
![]() $k\in \mathrm {ncl}_{\mathbb {N}_{\max }}(n)\subseteq S$
and
$k\in \mathrm {ncl}_{\mathbb {N}_{\max }}(n)\subseteq S$
and
![]() $S=\mathbb {N}$
.
$S=\mathbb {N}$
.
Example 2.24. It readily follows from Proposition 2.22 together with the simplicity of the alternating groups
![]() $A_n$
for each
$A_n$
for each
![]() $n\geq 5$
that the lattice of normal submonoids of
$n\geq 5$
that the lattice of normal submonoids of
![]() $T_n$
is given by the finite chain
$T_n$
is given by the finite chain
 $$ \begin{align*} \{1\}\subset S_2\subset T_2& \quad\mbox{if } n=2, \\ \{1\}\subset K_4\subset A_4\subset S_4\subset T_4& \quad\mbox{if } n=4, \\ \{1\}\subset A_n\subset S_n\subset T_n& \quad\mbox{if } n\neq 2,4, \end{align*} $$
$$ \begin{align*} \{1\}\subset S_2\subset T_2& \quad\mbox{if } n=2, \\ \{1\}\subset K_4\subset A_4\subset S_4\subset T_4& \quad\mbox{if } n=4, \\ \{1\}\subset A_n\subset S_n\subset T_n& \quad\mbox{if } n\neq 2,4, \end{align*} $$
with
![]() $K_4=\{\mathrm {id},(12)(34),(13)(24),(14)(32)\}$
the Klein permutation four-group.
$K_4=\{\mathrm {id},(12)(34),(13)(24),(14)(32)\}$
the Klein permutation four-group.
Definition 2.25. A monoid M is called modular if the lattice of normal submonoids
![]() $\mathsf {NorSub}(M)$
is modular (that is, if
$\mathsf {NorSub}(M)$
is modular (that is, if
![]() $S_1\vee (S_2\wedge S_3)=(S_1\vee S_2)\wedge S_3$
for all normal submonoids
$S_1\vee (S_2\wedge S_3)=(S_1\vee S_2)\wedge S_3$
for all normal submonoids
![]() $S_1S_2,S_3$
of M such that
$S_1S_2,S_3$
of M such that
![]() $S_1\subseteq S_3$
).
$S_1\subseteq S_3$
).
As is well known, every group is a modular monoid. Thus, the question arises whether every monoid is also modular, and in case it is not, determining what monoids, or families of monoids, are modular. The standard proof of the modularity of
![]() $\mathsf {NorSub}(G)$
for a group G makes use of the fact that the join of two normal subgroups is nothing but their product (see, for instance, [Reference Jacobson9, Theorem 8.3]). However, as a matter of fact, the equality
$\mathsf {NorSub}(G)$
for a group G makes use of the fact that the join of two normal subgroups is nothing but their product (see, for instance, [Reference Jacobson9, Theorem 8.3]). However, as a matter of fact, the equality
![]() $S\vee S'=SS'$
for all normal submonoids
$S\vee S'=SS'$
for all normal submonoids
![]() $S,S'$
of a monoid M is not necessary for
$S,S'$
of a monoid M is not necessary for
![]() $\mathsf {NorSub}(M)$
to be modular. Actually, there are modular monoids for which this equality does not hold for each
$\mathsf {NorSub}(M)$
to be modular. Actually, there are modular monoids for which this equality does not hold for each
![]() $S,S'$
. Even more,
$S,S'$
. Even more,
![]() $SS'$
need not be a normal submonoid at all when M is not a group.
$SS'$
need not be a normal submonoid at all when M is not a group.
Example 2.26. Let
![]() $M=\mathbb {N}_+$
. If
$M=\mathbb {N}_+$
. If
![]() $S=\langle 2\rangle $
and
$S=\langle 2\rangle $
and
![]() $S'=\langle 3\rangle $
, the product
$S'=\langle 3\rangle $
, the product
![]() $SS'$
, more properly denoted by
$SS'$
, more properly denoted by
![]() $S+S'$
in this case, is
$S+S'$
in this case, is
![]() $\langle 2\rangle +\langle 3\rangle =\mathbb {N}\setminus \{1\}$
, which is not a normal submonoid of
$\langle 2\rangle +\langle 3\rangle =\mathbb {N}\setminus \{1\}$
, which is not a normal submonoid of
![]() $\mathbb {N}_+$
. Hence,
$\mathbb {N}_+$
. Hence,
![]() $\langle 2\rangle \vee \langle 3\rangle \neq \langle 2\rangle +\langle 3\rangle $
. In spite of that,
$\langle 2\rangle \vee \langle 3\rangle \neq \langle 2\rangle +\langle 3\rangle $
. In spite of that,
![]() $\mathbb {N}_+$
is modular. Indeed, let
$\mathbb {N}_+$
is modular. Indeed, let
![]() $S_1,S_2,S$
be normal submonoids of
$S_1,S_2,S$
be normal submonoids of
![]() $\mathbb {N}_+$
, with
$\mathbb {N}_+$
, with
![]() $S_1\subseteq S_2$
. We have to see that
$S_1\subseteq S_2$
. We have to see that
![]() $(S_1\vee S)\wedge S_2=S_1\vee (S\wedge S_2)$
. Now, it follows from Proposition 2.9 that
$(S_1\vee S)\wedge S_2=S_1\vee (S\wedge S_2)$
. Now, it follows from Proposition 2.9 that
![]() $S_1=\langle nq\rangle $
,
$S_1=\langle nq\rangle $
,
![]() $S_2=\langle n\rangle $
, and
$S_2=\langle n\rangle $
, and
![]() $S=\langle m\rangle $
for some
$S=\langle m\rangle $
for some
![]() $m,n,q\geq 0$
. Moreover, from Example 2.16, we know that
$m,n,q\geq 0$
. Moreover, from Example 2.16, we know that
 $$ \begin{align*} (\langle nq\rangle\vee\langle m\rangle)\wedge\langle n\rangle&=\langle\gcd(nq,m)\rangle\cap\langle n\rangle=\langle\operatorname{\mathrm{lcm}}(\gcd(nq,m),n)\rangle \\ \langle nq\rangle\vee(\langle m\rangle\wedge\langle n\rangle)&=\langle nq\rangle\vee\langle\operatorname{\mathrm{lcm}}(m,n)\rangle=\langle\gcd(nq,\operatorname{\mathrm{lcm}}(m,n)\rangle. \end{align*} $$
$$ \begin{align*} (\langle nq\rangle\vee\langle m\rangle)\wedge\langle n\rangle&=\langle\gcd(nq,m)\rangle\cap\langle n\rangle=\langle\operatorname{\mathrm{lcm}}(\gcd(nq,m),n)\rangle \\ \langle nq\rangle\vee(\langle m\rangle\wedge\langle n\rangle)&=\langle nq\rangle\vee\langle\operatorname{\mathrm{lcm}}(m,n)\rangle=\langle\gcd(nq,\operatorname{\mathrm{lcm}}(m,n)\rangle. \end{align*} $$
Hence, we just need to see that
![]() $\operatorname {\mathrm {lcm}}(\gcd (nq,m),n)=\gcd (nq,\operatorname {\mathrm {lcm}}(m,n))$
, and this is a consequence of the general fact that
$\operatorname {\mathrm {lcm}}(\gcd (nq,m),n)=\gcd (nq,\operatorname {\mathrm {lcm}}(m,n))$
, and this is a consequence of the general fact that
![]() $\gcd (a,\operatorname {\mathrm {lcm}}(b, c)) =\operatorname {\mathrm {lcm}}(\gcd (a, b),\gcd (a, c))$
for each
$\gcd (a,\operatorname {\mathrm {lcm}}(b, c)) =\operatorname {\mathrm {lcm}}(\gcd (a, b),\gcd (a, c))$
for each
![]() $a,b,c$
.
$a,b,c$
.
As shown by this example, the modularity of a monoid M is a more subtle question than just knowing if the equality
![]() $S\vee S'=SS'$
holds for all normal submonoids
$S\vee S'=SS'$
holds for all normal submonoids
![]() $S,S'$
of M. The following result gives an infinite family of monoids M such that
$S,S'$
of M. The following result gives an infinite family of monoids M such that
![]() $\mathsf {NorSub}(M)$
is modular, a family that generalizes the monoid in Example 2.26.
$\mathsf {NorSub}(M)$
is modular, a family that generalizes the monoid in Example 2.26.
Theorem 2.27. Let
![]() $M=(M,+,0)$
be a cancellative commutative monoid such that
$M=(M,+,0)$
be a cancellative commutative monoid such that
Then
![]() $\mathsf {NorSub}(M)$
is isomorphic to the lattice
$\mathsf {NorSub}(M)$
is isomorphic to the lattice
![]() $\mathsf {Sub}(\widehat {M})$
of (normal) subgroups of the Grothendieck group
$\mathsf {Sub}(\widehat {M})$
of (normal) subgroups of the Grothendieck group
![]() $\widehat {M}$
of M. In particular, every cancellative commutative monoid satisfying
$\widehat {M}$
of M. In particular, every cancellative commutative monoid satisfying
![]() $(*)$
is modular.
$(*)$
is modular.
Proof. Since M is assumed to be cancellative,
![]() $\widehat {M}$
is given (up to isomorphism) by the quotient of the product monoid
$\widehat {M}$
is given (up to isomorphism) by the quotient of the product monoid
![]() $M\times M$
modulo the congruence relation
$M\times M$
modulo the congruence relation
We denote by
![]() $[m,n]$
the equivalence class of
$[m,n]$
the equivalence class of
![]() $(m,n)$
in
$(m,n)$
in
![]() $\widehat {M}$
. Then for every normal submonoid
$\widehat {M}$
. Then for every normal submonoid
![]() $S\lhd M$
, let
$S\lhd M$
, let
![]() $\widehat {S}$
be the subgroup of
$\widehat {S}$
be the subgroup of
![]() $\widehat {M}$
given by
$\widehat {M}$
given by
The notation is justified by the fact that this subgroup is indeed isomorphic to the Grothendieck group of S. This is again a consequence of the cancellative character of M, which ensures that
![]() $(s,s'),(t,t')\in S\times S$
are equivalent in the Grothendieck group of S if and only if they are equivalent in
$(s,s'),(t,t')\in S\times S$
are equivalent in the Grothendieck group of S if and only if they are equivalent in
![]() $\widehat {M}$
. Then let
$\widehat {M}$
. Then let
![]() $f:\mathsf {NorSub}(M)\to \mathsf {Sub}(\widehat {M})$
be the map defined by
$f:\mathsf {NorSub}(M)\to \mathsf {Sub}(\widehat {M})$
be the map defined by
![]() $S\mapsto \widehat {S}$
.
$S\mapsto \widehat {S}$
.
We claim that f is a lattice isomorphism. It is clearly order-preserving. Moreover, it is injective. Indeed, let
![]() $S_1,S_2\lhd M$
be such that
$S_1,S_2\lhd M$
be such that
![]() $\widehat {S}_1=\widehat {S}_2$
, and let
$\widehat {S}_1=\widehat {S}_2$
, and let
![]() $x\in S_1$
. Then
$x\in S_1$
. Then
![]() $[x,0]\in \widehat {S}_1$
and hence, we also have
$[x,0]\in \widehat {S}_1$
and hence, we also have
![]() $[x,0]\in \widehat {S}_2$
. However, this means that there exists a pair
$[x,0]\in \widehat {S}_2$
. However, this means that there exists a pair
![]() $(s_2,s^{\prime }_2)\in S_2\times S_2$
such that
$(s_2,s^{\prime }_2)\in S_2\times S_2$
such that
![]() $[x,0]=[s_2,s^{\prime }_2]$
, that is, such that
$[x,0]=[s_2,s^{\prime }_2]$
, that is, such that
![]() $x+s^{\prime }_2=s_2$
. It follows that x belongs to the left stability set of
$x+s^{\prime }_2=s_2$
. It follows that x belongs to the left stability set of
![]() $S_2$
and consequently,
$S_2$
and consequently,
![]() $x=x+0\in S_2$
because
$x=x+0\in S_2$
because
![]() $S_2$
is invariant. This proves that
$S_2$
is invariant. This proves that
![]() $S_1\subseteq S_2$
. A similar argument proves that
$S_1\subseteq S_2$
. A similar argument proves that
![]() $S_2\subseteq S_1$
and hence,
$S_2\subseteq S_1$
and hence,
![]() $S_1=S_2$
. To prove it is surjective, let
$S_1=S_2$
. To prove it is surjective, let
for every (normal) subgroup H of
![]() $\widehat {M}$
. We claim that
$\widehat {M}$
. We claim that
![]() $n(H)$
is a normal submonoid of M such that
$n(H)$
is a normal submonoid of M such that
Indeed, it is a groupal submonoid of M because H is a subgroup of
![]() $\widehat {M}$
. Moreover, let
$\widehat {M}$
. Moreover, let
![]() $z\in LX_{n(H)}$
so that
$z\in LX_{n(H)}$
so that
![]() $z+x\in n(H)$
for some
$z+x\in n(H)$
for some
![]() $x\in n(H)$
. This means that
$x\in n(H)$
. This means that
![]() $[z+x,0],[x,0]\in H$
and hence,
$[z+x,0],[x,0]\in H$
and hence,
is also in H. Therefore,
![]() $z\in n(H)$
and consequently,
$z\in n(H)$
and consequently,
![]() $z+n(H)\subseteq n(H)$
, that is,
$z+n(H)\subseteq n(H)$
, that is,
![]() $n(H)$
is invariant. Let us now prove Equation (2-9). The inclusion
$n(H)$
is invariant. Let us now prove Equation (2-9). The inclusion
![]() $\widehat {n(H)}\subseteq H$
holds even if M does not satisfy (*). Thus, if
$\widehat {n(H)}\subseteq H$
holds even if M does not satisfy (*). Thus, if
![]() $u\in \widehat {n(H)}$
, then
$u\in \widehat {n(H)}$
, then
![]() $u=[x,x']$
for some
$u=[x,x']$
for some
![]() $x,x'\in n(H)$
and hence, such that
$x,x'\in n(H)$
and hence, such that
![]() $[x,0],[x',0]\in H$
. Then,
$[x,0],[x',0]\in H$
. Then,
because H is a subgroup. It is to prove the reverse inclusion that condition (*) is needed. Thus, let
![]() $h\in H$
, that is,
$h\in H$
, that is,
![]() $h=[y,y']$
for some
$h=[y,y']$
for some
![]() $y,y'\in M$
. By condition (*), we have either
$y,y'\in M$
. By condition (*), we have either
![]() $y=y'+z$
or
$y=y'+z$
or
![]() $y'=y+z$
for some
$y'=y+z$
for some
![]() $z\in M$
. In the first case,
$z\in M$
. In the first case,
and hence,
![]() $z\in n(H)$
and
$z\in n(H)$
and
![]() $h=[z,0]\in \widehat {n(H)}$
. Similarly, in the second case,
$h=[z,0]\in \widehat {n(H)}$
. Similarly, in the second case,
and hence, also
![]() $[z,0]\in H$
because H is a subgroup. Consequently,
$[z,0]\in H$
because H is a subgroup. Consequently,
![]() $z\in n(H)$
and again
$z\in n(H)$
and again
![]() $h\in \widehat {n(H)}$
. This proves that f is a bijective order-preserving map. Since the inverse map
$h\in \widehat {n(H)}$
. This proves that f is a bijective order-preserving map. Since the inverse map
![]() $H\mapsto n(H)$
is also order-preserving, it follows that f is a lattice isomorphism. The last assertion then follows from the modularity of the lattice of normal subgroups of a group.
$H\mapsto n(H)$
is also order-preserving, it follows that f is a lattice isomorphism. The last assertion then follows from the modularity of the lattice of normal subgroups of a group.
Example 2.28. Every free commutative monoid is modular. Indeed, every free commutative monoid is cancellative and satisfies condition (*). More generally, let us recall that by a saturated submonoid S of a commutative monoid M, is meant a submonoid such that for every
![]() $s_1,s_2\in S$
and
$s_1,s_2\in S$
and
![]() $x\in M$
such that
$x\in M$
such that
![]() $s_1=s_2+x$
, we have
$s_1=s_2+x$
, we have
![]() $x\in S$
. Then every saturated submonoid of a free commutative monoid is also a cancellative commutative monoid satisfying condition (*) and hence, modular. Even more generally, every Krull monoid is modular, where by a Krull monoid, is meant a monoid isomorphic to
$x\in S$
. Then every saturated submonoid of a free commutative monoid is also a cancellative commutative monoid satisfying condition (*) and hence, modular. Even more generally, every Krull monoid is modular, where by a Krull monoid, is meant a monoid isomorphic to
![]() $A\times S$
for some abelian group A, and some saturated submonoid S of a free commutative monoid.
$A\times S$
for some abelian group A, and some saturated submonoid S of a free commutative monoid.
Let us emphasize that condition (*) is needed to prove that f is onto with inverse map given by
![]() $H\mapsto n(H)$
. For a generic cancellative commutative monoid, we have the following weaker version of Theorem 2.27.
$H\mapsto n(H)$
. For a generic cancellative commutative monoid, we have the following weaker version of Theorem 2.27.
Theorem 2.29. For every concellative commutative monoid M,
![]() $\mathsf {NorSub}(M)$
is isomorphic, as a join semilattice, to a join subsemilattice of
$\mathsf {NorSub}(M)$
is isomorphic, as a join semilattice, to a join subsemilattice of
![]() $\mathsf {Sub}(\widehat {M})$
.
$\mathsf {Sub}(\widehat {M})$
.
Proof. We have to see that the above injective map
![]() $f:\mathsf {NorSub}(M)\to \mathsf {Sub}(\widehat {M})$
is join-preserving. Let
$f:\mathsf {NorSub}(M)\to \mathsf {Sub}(\widehat {M})$
is join-preserving. Let
![]() $S_1,S_2\lhd M$
. The inclusion
$S_1,S_2\lhd M$
. The inclusion
![]() $\widehat {S}_1\vee \widehat {S}_2\subseteq \widehat {S_1\vee S}_2$
follows because f is order-preserving, and
$\widehat {S}_1\vee \widehat {S}_2\subseteq \widehat {S_1\vee S}_2$
follows because f is order-preserving, and
![]() $\widehat {S}_1\vee \widehat {S}_2$
is the smallest subgroup containing both
$\widehat {S}_1\vee \widehat {S}_2$
is the smallest subgroup containing both
![]() $\widehat {S}_1$
and
$\widehat {S}_1$
and
![]() $\widehat {S}_2$
. To prove the reverse inclusion, let
$\widehat {S}_2$
. To prove the reverse inclusion, let
![]() $x\in \widehat {S_1\vee S}_2$
. This means that
$x\in \widehat {S_1\vee S}_2$
. This means that
![]() $x=[t,t']$
for some
$x=[t,t']$
for some
![]() $t,t'\in S_1\vee S_2$
. Since
$t,t'\in S_1\vee S_2$
. Since
![]() $\widehat {S}_1\vee \widehat {S}_2=\widehat {S}_1+\widehat {S}_2$
, we have to see that
$\widehat {S}_1\vee \widehat {S}_2=\widehat {S}_1+\widehat {S}_2$
, we have to see that
for some pairs
![]() $(s_1,s^{\prime }_1)\in S_1\times S_1$
and
$(s_1,s^{\prime }_1)\in S_1\times S_1$
and
![]() $(s_2,s^{\prime }_2)\in S_2\times S_2$
. To prove this, recall that
$(s_2,s^{\prime }_2)\in S_2\times S_2$
. To prove this, recall that
with
![]() $(S_1\cup S_2)_n$
the sequence of groupal submonoids recursively defined by
$(S_1\cup S_2)_n$
the sequence of groupal submonoids recursively defined by
 $$ \begin{align*} (S_1\cup S_2)_0&=\langle S_1\cup S_2\rangle', \\ (S_1\cup S_2)_n&=\bigg\langle\bigcup_{z\in LX_{(S_1\cup S_2)_{n-1}}}(z+(S_1\cup S_2)_{n-1})\bigg\rangle',\quad n\geq 1 \end{align*} $$
$$ \begin{align*} (S_1\cup S_2)_0&=\langle S_1\cup S_2\rangle', \\ (S_1\cup S_2)_n&=\bigg\langle\bigcup_{z\in LX_{(S_1\cup S_2)_{n-1}}}(z+(S_1\cup S_2)_{n-1})\bigg\rangle',\quad n\geq 1 \end{align*} $$
(see Section 2.2). Since the sequence
![]() $(S_1\cup S_2)_n$
is a nondecreasing chain,
$(S_1\cup S_2)_n$
is a nondecreasing chain,
![]() $t,t'\in S_1\vee S_2$
implies that
$t,t'\in S_1\vee S_2$
implies that
![]() $t,t'\in (S_1\cup S_2)_n$
for some
$t,t'\in (S_1\cup S_2)_n$
for some
![]() $n\geq 0$
. Then we prove Equation (2-10) by induction on
$n\geq 0$
. Then we prove Equation (2-10) by induction on
![]() $n\geq 0$
. If
$n\geq 0$
. If
![]() $n=0$
, we have
$n=0$
, we have
![]() $t,t'\in \langle S_1\cup S_2\rangle $
because both
$t,t'\in \langle S_1\cup S_2\rangle $
because both
![]() $S_1,S_2$
are groupal submonoids. Hence, both are finite sums of elements in
$S_1,S_2$
are groupal submonoids. Hence, both are finite sums of elements in
![]() $S_1$
and/or
$S_1$
and/or
![]() $S_2$
. By the commutativity of M, it follows that
$S_2$
. By the commutativity of M, it follows that
![]() $(t,t')$
is in fact equal to a pair as in the right-hand side of Equation (2-10). Let us now assume that for some
$(t,t')$
is in fact equal to a pair as in the right-hand side of Equation (2-10). Let us now assume that for some
![]() $n\geq 1$
, every pair
$n\geq 1$
, every pair
![]() $(u,u')$
with
$(u,u')$
with
![]() $u,u'\in (S_1\cup S_2)_{n-1}$
is equivalent to a pair as in the right-hand side of Equation (2-10), and let
$u,u'\in (S_1\cup S_2)_{n-1}$
is equivalent to a pair as in the right-hand side of Equation (2-10), and let
![]() $t,t'\in (S_1\cup S_2)_n$
. This means that there exist
$t,t'\in (S_1\cup S_2)_n$
. This means that there exist
![]() $z_1,\ldots ,z_{k+l},z^{\prime }_1,\ldots ,z^{\prime }_{k'+l'}\in LX_{(S_1\cup S_2)_{n-1}}$
and
$z_1,\ldots ,z_{k+l},z^{\prime }_1,\ldots ,z^{\prime }_{k'+l'}\in LX_{(S_1\cup S_2)_{n-1}}$
and
![]() $u_1,\ldots ,u_{k+l},u^{\prime }_1,\ldots ,u^{\prime }_{k'+l'}\in (S_1\cup S_2)_{n-1}$
such that
$u_1,\ldots ,u_{k+l},u^{\prime }_1,\ldots ,u^{\prime }_{k'+l'}\in (S_1\cup S_2)_{n-1}$
such that
![]() $z_{i}+u_{i},z^{\prime }_{i'}+u^{\prime }_{i'}$
are invertible for each
$z_{i}+u_{i},z^{\prime }_{i'}+u^{\prime }_{i'}$
are invertible for each
![]() $i\in \{k+1,\ldots ,k+l\}$
and
$i\in \{k+1,\ldots ,k+l\}$
and
![]() $i'\in \{k'+1,\ldots ,k'+l'\}$
, and
$i'\in \{k'+1,\ldots ,k'+l'\}$
, and
![]() $(t,t')=(A+B,A'+B')$
with
$(t,t')=(A+B,A'+B')$
with
 $$ \begin{align*} A&=(z_1+u_1)+\cdots+(z_k+u_k), \\ A'&=(z^{\prime}_1+u^{\prime}_1)+\cdots+(z^{\prime}_{k'}+u^{\prime}_{k'}), \\ B&=[-(z_{k+1}+u_{k+1})]+\cdots+[-(z_{k+l}+u_{k+l})], \\ B'&=[-(z^{\prime}_{k'+1}+u^{\prime}_{k'+1})]+\cdots+[-(z^{\prime}_{k'+l'}+u^{\prime}_{k'+l'})] \end{align*} $$
$$ \begin{align*} A&=(z_1+u_1)+\cdots+(z_k+u_k), \\ A'&=(z^{\prime}_1+u^{\prime}_1)+\cdots+(z^{\prime}_{k'}+u^{\prime}_{k'}), \\ B&=[-(z_{k+1}+u_{k+1})]+\cdots+[-(z_{k+l}+u_{k+l})], \\ B'&=[-(z^{\prime}_{k'+1}+u^{\prime}_{k'+1})]+\cdots+[-(z^{\prime}_{k'+l'}+u^{\prime}_{k'+l'})] \end{align*} $$
(here we are using the commutativity of M to write first all ‘positive terms’ in the expressions of both
![]() $t,t'$
). However,
$t,t'$
). However,
 $$ \begin{align*} (t,t')&=(A+B,A'+B') \\ &\sim(A+B,A'+B')+((-B)+(-B'),(-B)+(-B')) \\ &=(A+(-B'),A'+(-B)). \end{align*} $$
$$ \begin{align*} (t,t')&=(A+B,A'+B') \\ &\sim(A+B,A'+B')+((-B)+(-B'),(-B)+(-B')) \\ &=(A+(-B'),A'+(-B)). \end{align*} $$
Moreover, since M is commutative, and both
![]() $LX_{(S_1\cup S_2)_{n-1}}$
and
$LX_{(S_1\cup S_2)_{n-1}}$
and
![]() $(S_1\cup S_2)_{n-1}$
are submonoids, reordering terms,
$(S_1\cup S_2)_{n-1}$
are submonoids, reordering terms,
 $$ \begin{align*} A+(-B')&=y+v, \\ A'+(-B)&=y'+v', \end{align*} $$
$$ \begin{align*} A+(-B')&=y+v, \\ A'+(-B)&=y'+v', \end{align*} $$
with
![]() $y\in LX_{(S_1\cup S_2)_{n-1}}$
,
$y\in LX_{(S_1\cup S_2)_{n-1}}$
,
![]() $v\in (S_1\cup S_2)_{n-1}$
given by
$v\in (S_1\cup S_2)_{n-1}$
given by
 $$ \begin{align*} y&=z_1+\cdots+z_k+z^{\prime}_{k'+1}+\cdots+z^{\prime}_{k'+l'}, \\ v&=u_1+\cdots+u_k+u^{\prime}_{k'+1}+\cdots+u^{\prime}_{k'+l'}, \end{align*} $$
$$ \begin{align*} y&=z_1+\cdots+z_k+z^{\prime}_{k'+1}+\cdots+z^{\prime}_{k'+l'}, \\ v&=u_1+\cdots+u_k+u^{\prime}_{k'+1}+\cdots+u^{\prime}_{k'+l'}, \end{align*} $$
and similarly
![]() $y',v'$
. Now, since
$y',v'$
. Now, since
![]() $y,y'\in LX_{(S_1\cup S_2)_{n-1}}$
, there exists
$y,y'\in LX_{(S_1\cup S_2)_{n-1}}$
, there exists
![]() $w,w'\in (S_1\cup S_2)_{n-1}$
such that
$w,w'\in (S_1\cup S_2)_{n-1}$
such that
![]() $y+w,y'+w'\in (S_1\cup S_2)_{n-1}$
. Therefore,
$y+w,y'+w'\in (S_1\cup S_2)_{n-1}$
. Therefore,
By the induction hypothesis, it follows that
![]() $(t,t')$
is also equivalent to a pair as in the right-hand side of Equation (2-10). Hence,
$(t,t')$
is also equivalent to a pair as in the right-hand side of Equation (2-10). Hence,
and
![]() $\widehat {S}_1\vee \widehat {S}_2\supseteq \widehat {S_1\vee S}_2$
.
$\widehat {S}_1\vee \widehat {S}_2\supseteq \widehat {S_1\vee S}_2$
.
Remark 2.30. It seems that for a generic cancellative commutative monoid M, the lattice
![]() $\mathsf {NorSub}(M)$
is not isomorphic through the injection f to a sublattice of
$\mathsf {NorSub}(M)$
is not isomorphic through the injection f to a sublattice of
![]() $\mathsf {Sub}(\widehat {M})$
, a fact that implies the modularity of M also in this more general case. The problem is that condition (*) seems to be also necessary to prove that f is meet-preserving, and not just onto. Indeed, the inclusion
$\mathsf {Sub}(\widehat {M})$
, a fact that implies the modularity of M also in this more general case. The problem is that condition (*) seems to be also necessary to prove that f is meet-preserving, and not just onto. Indeed, the inclusion
![]() $\widehat {S_1\cap S}_2\subseteq \widehat {S}_1\cap \widehat {S}_2$
is always true because
$\widehat {S_1\cap S}_2\subseteq \widehat {S}_1\cap \widehat {S}_2$
is always true because
![]() $S_1\cap S_2\subseteq S_1,S_2$
and hence,
$S_1\cap S_2\subseteq S_1,S_2$
and hence,
![]() $\widehat {S_1\cap S}_2$
is a subgroup contained in both
$\widehat {S_1\cap S}_2$
is a subgroup contained in both
![]() $\widehat {S}_1$
and
$\widehat {S}_1$
and
![]() $\widehat {S}_1$
. However, to prove the reverse inclusion, we have to see that every time we have
$\widehat {S}_1$
. However, to prove the reverse inclusion, we have to see that every time we have
![]() $u=[s_1,s^{\prime }_1]=[s_2,s^{\prime }_2]$
for some pairs
$u=[s_1,s^{\prime }_1]=[s_2,s^{\prime }_2]$
for some pairs
![]() $(s_1,s^{\prime }_1)\in S_1\times S_1$
and
$(s_1,s^{\prime }_1)\in S_1\times S_1$
and
![]() $(s_2,s^{\prime }_2)\in S_2\times S_2$
, there is a pair
$(s_2,s^{\prime }_2)\in S_2\times S_2$
, there is a pair
![]() $(x,y)$
with
$(x,y)$
with
![]() $x,y\in S_1\cap S_2$
whose equivalence class is u. Using hypothesis (*), this is easily shown. For instance, if
$x,y\in S_1\cap S_2$
whose equivalence class is u. Using hypothesis (*), this is easily shown. For instance, if
![]() $s_1=x+s^{\prime }_1$
or
$s_1=x+s^{\prime }_1$
or
![]() $s^{\prime }_1=x+s_1$
for some
$s^{\prime }_1=x+s_1$
for some
![]() $x\in M$
, then
$x\in M$
, then
![]() $x\in LX_{S_1}$
and hence,
$x\in LX_{S_1}$
and hence,
![]() $x\in S_1$
because
$x\in S_1$
because
![]() $S_1$
is invariant. In other words, we have either
$S_1$
is invariant. In other words, we have either
![]() $u=[x,0]$
or
$u=[x,0]$
or
![]() $u=[0,x]$
for some
$u=[0,x]$
for some
![]() $x\in S_1$
. Similarly, the invariance of
$x\in S_1$
. Similarly, the invariance of
![]() $S_2$
shows that either
$S_2$
shows that either
![]() $u=[y,0]$
or
$u=[y,0]$
or
![]() $u=[0,y]$
for some
$u=[0,y]$
for some
![]() $y\in S_2$
. It is now easy to see that in either case, we have
$y\in S_2$
. It is now easy to see that in either case, we have
![]() $x,y\in S_1\cap S_2$
and hence, that
$x,y\in S_1\cap S_2$
and hence, that
![]() $u\in \widehat {S_1\cap S_2}$
. For instance, if
$u\in \widehat {S_1\cap S_2}$
. For instance, if
![]() $u=[x,0]=[y,0]$
, we have
$u=[x,0]=[y,0]$
, we have
![]() $x=y$
, while
$x=y$
, while
![]() $u=[x,0]=[0,y]$
implies that
$u=[x,0]=[0,y]$
implies that
![]() $x+y=0$
, that is, y is the opposite of x and hence, we also have
$x+y=0$
, that is, y is the opposite of x and hence, we also have
![]() $y\in S_1$
because
$y\in S_1$
because
![]() $S_1$
is groupal. However, it is not clear that without assuming condition (*), the reverse inclusion is still true.
$S_1$
is groupal. However, it is not clear that without assuming condition (*), the reverse inclusion is still true.
3 On the lattice of congruences on a monoid
As recalled in the introduction, the lattice of congruences on a group G is isomorphic to the lattice of normal subgroups of G. The purpose of this section is to prove a weaker version of this result valid for a generic monoid M. More precisely, we see that
![]() $\mathsf {NorSub}(M)$
embeds canonically into the set of congruences on M, and that this embedding is an isomorphism of join semilattices between
$\mathsf {NorSub}(M)$
embeds canonically into the set of congruences on M, and that this embedding is an isomorphism of join semilattices between
![]() $\mathsf {NorSub}(M)$
and the join subsemilattice of the so called ‘normal congruences’ on M. We also describe a general procedure to compute the ‘blow up’ of
$\mathsf {NorSub}(M)$
and the join subsemilattice of the so called ‘normal congruences’ on M. We also describe a general procedure to compute the ‘blow up’ of
![]() $\mathsf {NorSub}(M)$
giving the whole lattice of congruences on M. As we see, it basically reduces the problem of finding all congruences to being able to compute the unital ones.
$\mathsf {NorSub}(M)$
giving the whole lattice of congruences on M. As we see, it basically reduces the problem of finding all congruences to being able to compute the unital ones.
In what follows,
![]() $\mathsf {Cong}(M)$
denotes the set of congruences on a monoid M. When ordered by inclusion, it is a complete lattice with meets and joins respectively given by
$\mathsf {Cong}(M)$
denotes the set of congruences on a monoid M. When ordered by inclusion, it is a complete lattice with meets and joins respectively given by
 $$ \begin{align*} \bigwedge_{i\in I}R_i&=\bigcap_{i\in I}R_i, \\ \bigvee_{i\in I}R_i&=\bigg(\bigcup_{i\in I}R_i\bigg)^\sharp \end{align*} $$
$$ \begin{align*} \bigwedge_{i\in I}R_i&=\bigcap_{i\in I}R_i, \\ \bigvee_{i\in I}R_i&=\bigg(\bigcup_{i\in I}R_i\bigg)^\sharp \end{align*} $$
for any family of congruences
![]() $\{R_i\}_{i\in I}$
on M. Here,
$\{R_i\}_{i\in I}$
on M. Here,
![]() $Y^\sharp $
for every subset
$Y^\sharp $
for every subset
![]() $Y\subseteq M\times M$
denotes the smallest congruence on M containing Y. Explicitly, it is the equivalence relation on M generated by the subset
$Y\subseteq M\times M$
denotes the smallest congruence on M containing Y. Explicitly, it is the equivalence relation on M generated by the subset
![]() $\{(xay,xby),\,(a,b)\in Y : x,y\in M\}$
(see [Reference Howie8, Proposition 1.5.8] or [Reference Cain1, Propositions 1.27 and 1.29]).
$\{(xay,xby),\,(a,b)\in Y : x,y\in M\}$
(see [Reference Howie8, Proposition 1.5.8] or [Reference Cain1, Propositions 1.27 and 1.29]).
3.1 Congruence induced by a subset
For every subset
![]() $A\subseteq M$
, let us denote by
$A\subseteq M$
, let us denote by
![]() $\mathsf {Cong}(M,A)$
the subset of
$\mathsf {Cong}(M,A)$
the subset of
![]() $\mathsf {Cong}(M)$
consisting of the congruences R such that
$\mathsf {Cong}(M)$
consisting of the congruences R such that
![]() $A\subseteq [1]_R$
. Notice that both the meet and join in
$A\subseteq [1]_R$
. Notice that both the meet and join in
![]() $\mathsf {Cong}(M)$
of a family of congruences in
$\mathsf {Cong}(M)$
of a family of congruences in
![]() $\mathsf {Cong}(M,A)$
still are in
$\mathsf {Cong}(M,A)$
still are in
![]() $\mathsf {Cong}(M,A)$
. Hence,
$\mathsf {Cong}(M,A)$
. Hence,
![]() $\mathsf {Cong}(M,A)$
is a complete sublattice of
$\mathsf {Cong}(M,A)$
is a complete sublattice of
![]() $\mathsf {Cong}(M)$
. Let
$\mathsf {Cong}(M)$
. Let
![]() $R_A$
be the least element in
$R_A$
be the least element in
![]() $\mathsf {Cong}(M,A)$
, that is,
$\mathsf {Cong}(M,A)$
, that is,
It is called the congruence on M induced by A. Explicitly,
![]() $R_A$
is given as follows. If
$R_A$
is given as follows. If
![]() $v,w\in M$
, we say that w is an elementary A-deformation of v, and we write
$v,w\in M$
, we say that w is an elementary A-deformation of v, and we write
if there exists
![]() $v_1,v_2\in M$
, and
$v_1,v_2\in M$
, and
![]() $a\in A$
such that
$a\in A$
such that
![]() $v=v_1v_2$
, and
$v=v_1v_2$
, and
![]() $w=v_1av_2$
. Then
$w=v_1av_2$
. Then
![]() $(x,y)\in R_A$
if and only if there exists a finite sequence
$(x,y)\in R_A$
if and only if there exists a finite sequence
![]() $z_0,\ldots ,z_{k}$
of elements in M, with
$z_0,\ldots ,z_{k}$
of elements in M, with
![]() $k\geq 0$
, such that:
$k\geq 0$
, such that:
-
(a)
 $z_0=x$
and
$z_0=x$
and
 $z_{k}=y$
;
$z_{k}=y$
; -
(b) for each
 $i\in \{0,1,\ldots ,k-1\}$
, either
$i\in \{0,1,\ldots ,k-1\}$
, either
 $z_i\rightsquigarrow z_{i+1}$
or
$z_i\rightsquigarrow z_{i+1}$
or
 $z_{i+1}\rightsquigarrow z_i$
.
$z_{i+1}\rightsquigarrow z_i$
.
Since every element in M is an elementary A-deformation of itself, this is equivalent to the existence of a finite sequence
![]() $z_0,\ldots ,z_{2k}$
, with
$z_0,\ldots ,z_{2k}$
, with
![]() $k\geq 0$
, satisfying condition (a) above, and such that
$k\geq 0$
, satisfying condition (a) above, and such that
Example 3.1. Let
![]() $M=\mathbb {N}_+$
. Then
$M=\mathbb {N}_+$
. Then
![]() $R_{\langle n\rangle }$
,
$R_{\langle n\rangle }$
,
![]() $n\geq 1$
, is nothing but the usual congruence modulo n. Indeed, a positive integer
$n\geq 1$
, is nothing but the usual congruence modulo n. Indeed, a positive integer
![]() $l\geq 0$
is an elementary
$l\geq 0$
is an elementary
![]() $\langle n\rangle $
-deformation of
$\langle n\rangle $
-deformation of
![]() $k\geq 0$
if and only if
$k\geq 0$
if and only if
![]() $l\geq k$
, and
$l\geq k$
, and
![]() $l-k\in \langle n\rangle $
. Moreover, if l is an elementary
$l-k\in \langle n\rangle $
. Moreover, if l is an elementary
![]() $\langle n\rangle $
-deformation of both k and
$\langle n\rangle $
-deformation of both k and
![]() $k'$
, and
$k'$
, and
![]() $k'\geq k$
, then
$k'\geq k$
, then
![]() $k'$
is an elementary
$k'$
is an elementary
![]() $\langle n\rangle $
-deformation of k. Therefore,
$\langle n\rangle $
-deformation of k. Therefore,
![]() $(x,y)\in R_{\langle n\rangle }$
if and only if
$(x,y)\in R_{\langle n\rangle }$
if and only if
![]() $x,y$
differ by a multiple of n.
$x,y$
differ by a multiple of n.
In fact, in the commutative case, and when A is a subsemigroup of M, as is the case in the previous example, the congruence
![]() $R_A$
is more easily described as follows.
$R_A$
is more easily described as follows.
Proposition 3.2. Let M be a commutative monoid, A a subsemigroup of M, and
![]() $x,y\in M$
. Then
$x,y\in M$
. Then
![]() $(x,y)\in R_A$
if and only if there exists
$(x,y)\in R_A$
if and only if there exists
![]() $a,a'\in A$
such that
$a,a'\in A$
such that
![]() $x+a=y+a'$
.
$x+a=y+a'$
.
Proof. If M is commutative, we clearly have that
![]() $v\in M$
is an elementary A-deformation of
$v\in M$
is an elementary A-deformation of
![]() $u\in M$
if and only if
$u\in M$
if and only if
![]() $v=u+a$
for some
$v=u+a$
for some
![]() $a\in A$
. Hence, if
$a\in A$
. Hence, if
![]() $x+a=y+a'$
for some
$x+a=y+a'$
for some
![]() $a,a'\in A$
, then we have
$a,a'\in A$
, then we have ![]() and
and
![]() $(x,y)\in R_A$
. Conversely, let
$(x,y)\in R_A$
. Conversely, let
![]() $(x,y)\in R_A$
. Then there exists a sequence
$(x,y)\in R_A$
. Then there exists a sequence
![]() $z_0,\ldots ,z_{2k}$
as before. If
$z_0,\ldots ,z_{2k}$
as before. If
![]() $k=1$
, we have
$k=1$
, we have
![]() $x+a=y+a'$
for some
$x+a=y+a'$
for some
![]() $a,a'\in R$
. The cases
$a,a'\in R$
. The cases
![]() $k\geq 2$
follow then by induction on k together with the fact that A is closed under sums. Thus, let us assume that
$k\geq 2$
follow then by induction on k together with the fact that A is closed under sums. Thus, let us assume that
![]() $z_0+a_0=z_{2k-2}+a_1$
for some
$z_0+a_0=z_{2k-2}+a_1$
for some
![]() $a_0,a_1$
. Then from the case
$a_0,a_1$
. Then from the case
![]() $k=1$
, it follows that we also have
$k=1$
, it follows that we also have
![]() $z_{2k-2}+a^{\prime }_1=z_{2k}+a_2$
for some
$z_{2k-2}+a^{\prime }_1=z_{2k}+a_2$
for some
![]() $a^{\prime }_1,a_2\in A$
. Hence,
$a^{\prime }_1,a_2\in A$
. Hence,
with
![]() $a_0+a^{\prime }_1,a_1+a_2\in A$
.
$a_0+a^{\prime }_1,a_1+a_2\in A$
.
Clearly, if
![]() $M\neq \{1\}$
, the assignments
$M\neq \{1\}$
, the assignments
![]() $A\mapsto R_A$
are not one-to-one. Thus, for each
$A\mapsto R_A$
are not one-to-one. Thus, for each
![]() $A\subsetneq M$
with
$A\subsetneq M$
with
![]() $1\notin A$
, we have
$1\notin A$
, we have
![]() $R_A=R_{A\cup \{1\}}$
. In fact,
$R_A=R_{A\cup \{1\}}$
. In fact,
![]() $R_A$
depends on A only through its normal closure so that subsets of M having the same normal closure induce the same congruence. Actually, the converse is also true. To prove these claims, we need the following invariance properties of
$R_A$
depends on A only through its normal closure so that subsets of M having the same normal closure induce the same congruence. Actually, the converse is also true. To prove these claims, we need the following invariance properties of
![]() $\mathsf {Cong}(M,A)$
with respect to the subset A.
$\mathsf {Cong}(M,A)$
with respect to the subset A.
Proposition 3.3. Let A be any subset of M. Then:
-
(a)
 $\mathsf {Cong}(M,A)=\mathsf {Cong}(M,\langle A\rangle ')$
, with
$\mathsf {Cong}(M,A)=\mathsf {Cong}(M,\langle A\rangle ')$
, with
 $\langle A\rangle '$
the groupal submonoid of M generated by A;
$\langle A\rangle '$
the groupal submonoid of M generated by A; -
(b)
 $\mathsf {Cong}(M,A)=\mathsf {Cong}(M,xAy)$
for every
$\mathsf {Cong}(M,A)=\mathsf {Cong}(M,xAy)$
for every
 $(x,y)\in X_A$
.
$(x,y)\in X_A$
.
Proof. Clearly,
![]() $\mathsf {Cong}(M,A)\supseteq \mathsf {Cong}(M,\langle A\rangle ')$
because
$\mathsf {Cong}(M,A)\supseteq \mathsf {Cong}(M,\langle A\rangle ')$
because
![]() $A\subseteq \langle A\rangle '$
. To prove the reverse inclusion, let
$A\subseteq \langle A\rangle '$
. To prove the reverse inclusion, let
![]() $R\in \mathsf {Cong}(M)$
be such that
$R\in \mathsf {Cong}(M)$
be such that
![]() $A\subseteq [1]_R$
. Then for every
$A\subseteq [1]_R$
. Then for every
![]() $a_1,a_2\in A$
, we have
$a_1,a_2\in A$
, we have
![]() $(1,a_1),(1,a_2)\in R$
and hence,
$(1,a_1),(1,a_2)\in R$
and hence,
Moreover, if
![]() $a\in A$
is invertible, we have
$a\in A$
is invertible, we have
![]() $(a^{-1},a^{-1}),(1,a)\in R$
and hence,
$(a^{-1},a^{-1}),(1,a)\in R$
and hence,
Since every element in
![]() $\langle A\rangle '$
is a finite product of elements of A and/or their inverses (when they exist), it follows that
$\langle A\rangle '$
is a finite product of elements of A and/or their inverses (when they exist), it follows that
![]() $[1]_R$
also contains
$[1]_R$
also contains
![]() $\langle A\rangle '$
. This proves item (a). As for item (b), the inclusion
$\langle A\rangle '$
. This proves item (a). As for item (b), the inclusion
![]() $\mathsf {Cong}(M,A)\supseteq \mathsf {Cong}(M,xAy)$
is again obvious. To prove the reverse inclusion, let
$\mathsf {Cong}(M,A)\supseteq \mathsf {Cong}(M,xAy)$
is again obvious. To prove the reverse inclusion, let
![]() $R\in \mathsf {Cong}(M)$
be such that
$R\in \mathsf {Cong}(M)$
be such that
![]() $[1]_R$
contains A, and let
$[1]_R$
contains A, and let
![]() $(x,y)\in X_A$
. Then there exists
$(x,y)\in X_A$
. Then there exists
![]() $a_1,a_2\in A$
such that
$a_1,a_2\in A$
such that
![]() $xa_1y=a_2$
, and
$xa_1y=a_2$
, and
![]() $(a_1,1),(1,a_2)\in R$
by hypothesis. Then for every
$(a_1,1),(1,a_2)\in R$
by hypothesis. Then for every
![]() $a\in A$
, we have
$a\in A$
, we have
![]() $(1,a)\in R$
and hence,
$(1,a)\in R$
and hence,
![]() $(a_1,a)=(a_1,1)(1,a)\in R$
. Therefore,
$(a_1,a)=(a_1,1)(1,a)\in R$
. Therefore,
By transitivity, we conclude that
![]() $(1,xay)\in R$
. Since this is true for each
$(1,xay)\in R$
. Since this is true for each
![]() $a\in A$
and for each
$a\in A$
and for each
![]() $(x,y)\in X_A$
, it follows that
$(x,y)\in X_A$
, it follows that
![]() $[1]_R$
also contains every generalized conjugate of A.
$[1]_R$
also contains every generalized conjugate of A.
Proposition 3.4. For every monoid M and every subset A of M,
and consequently,
![]() $R_A=R_{\mathrm {ncl}(A)}$
.
$R_A=R_{\mathrm {ncl}(A)}$
.
Proof. The inclusion
![]() $\mathsf {Cong}(M,\mathrm {ncl}(A))\subseteq \mathsf {Cong}(M,A)$
is obvious. To prove the reverse inclusion, let us assume that
$\mathsf {Cong}(M,\mathrm {ncl}(A))\subseteq \mathsf {Cong}(M,A)$
is obvious. To prove the reverse inclusion, let us assume that
![]() $R\in \mathsf {Cong}(M,A)$
. Then an easy induction on
$R\in \mathsf {Cong}(M,A)$
. Then an easy induction on
![]() $n\geq 0$
using Lemma 3.3 shows that
$n\geq 0$
using Lemma 3.3 shows that
![]() $R\in \mathsf {Cong}(M,A_n)$
for each
$R\in \mathsf {Cong}(M,A_n)$
for each
![]() $n\geq 0$
, where
$n\geq 0$
, where
![]() $A_n$
is the sequence of groupal submonoids of M defined by Equations (2-3)–(2-4). Since
$A_n$
is the sequence of groupal submonoids of M defined by Equations (2-3)–(2-4). Since
![]() $\mathrm {ncl}(A)$
is the union of all
$\mathrm {ncl}(A)$
is the union of all
![]() $A_n$
’s (compare with Proposition 2.15 above), it follows that
$A_n$
’s (compare with Proposition 2.15 above), it follows that
![]() $R\in \mathsf {Cong}(M,\mathrm {ncl}(A))$
. The last assertion follows from the fact that
$R\in \mathsf {Cong}(M,\mathrm {ncl}(A))$
. The last assertion follows from the fact that
![]() $R_A$
is the minimum of the sublattice
$R_A$
is the minimum of the sublattice
![]() $\mathsf {Cong}(M,A)$
, and
$\mathsf {Cong}(M,A)$
, and
![]() $R_{\mathrm {ncl}(A)}$
is the minimum of
$R_{\mathrm {ncl}(A)}$
is the minimum of
![]() $\mathsf {Cong}(M,\mathrm {ncl}(A))$
.
$\mathsf {Cong}(M,\mathrm {ncl}(A))$
.
3.2 Embedding the set of normal submonoids into the set of congruences
Proposition 3.4 implies that subsets of M having the same normal closure induce the same congruence. Actually, the converse is also true. In fact, we claim that the map
![]() $\Phi _M:\mathsf {NorSub}(M)\to \mathsf {Cong}(M)$
sending each normal submonoid
$\Phi _M:\mathsf {NorSub}(M)\to \mathsf {Cong}(M)$
sending each normal submonoid
![]() $S\lhd M$
to the congruence
$S\lhd M$
to the congruence
![]() $R_S$
induced by S is one-to-one, from which the above converse readily follows. To prove this, we first need the following analog to a well-known fact about the congruences on a group.
$R_S$
induced by S is one-to-one, from which the above converse readily follows. To prove this, we first need the following analog to a well-known fact about the congruences on a group.
Proposition 3.5. For every congruence R on a monoid M, the identity element equivalence class
![]() $[1]_R$
is a normal submonoid of M.
$[1]_R$
is a normal submonoid of M.
Proof. Clearly,
![]() $[1]_R$
is a groupal submonoid of M because of the compatibility of R. To see that it is invariant, let
$[1]_R$
is a groupal submonoid of M because of the compatibility of R. To see that it is invariant, let
![]() $(x,y)\in X_{[1]_R}$
. This means that there exist
$(x,y)\in X_{[1]_R}$
. This means that there exist
![]() $z,z'\in [1]_R$
such that
$z,z'\in [1]_R$
such that
![]() $xzy=z'$
. Then by the compatibility of R,
$xzy=z'$
. Then by the compatibility of R,
that is,
![]() $xy\in [1]_R$
. Therefore, for each
$xy\in [1]_R$
. Therefore, for each
![]() $z_1\in [1]_R$
, we have
$z_1\in [1]_R$
, we have
![]() $[xz_1y]_R=[xy]_R=[1]_R$
, that is,
$[xz_1y]_R=[xy]_R=[1]_R$
, that is,
![]() $x[1]_Ry\subseteq [1]_R$
.
$x[1]_Ry\subseteq [1]_R$
.
Then let
![]() $\Psi _M:\mathsf {Cong}(M)\to \mathsf {NorSub}(M)$
be the map given by
$\Psi _M:\mathsf {Cong}(M)\to \mathsf {NorSub}(M)$
be the map given by
![]() $R\mapsto [1]_R$
. If M is a group G, we know that
$R\mapsto [1]_R$
. If M is a group G, we know that
![]() $\Phi _G$
is a lattice isomorphism with inverse
$\Phi _G$
is a lattice isomorphism with inverse
![]() $\Psi _G$
. Although this is no longer true for arbitrary monoids, the following weaker facts still remain true in the general setting.
$\Psi _G$
. Although this is no longer true for arbitrary monoids, the following weaker facts still remain true in the general setting.
Theorem 3.6. Let M be a monoid. Then:
-
(a)
 $\Phi _M$
(respectively
$\Phi _M$
(respectively
 $\Psi _M$
) is a join-homomorphism (respectively a meet-homo- morphism);
$\Psi _M$
) is a join-homomorphism (respectively a meet-homo- morphism); -
(b)
 $\Phi _M$
is a (set-theoretic) section of
$\Phi _M$
is a (set-theoretic) section of
 $\Psi _M$
. In particular, it is one-to-one.
$\Psi _M$
. In particular, it is one-to-one.
Proof. The map
![]() $\Phi _M$
is order-preserving. Thus, if
$\Phi _M$
is order-preserving. Thus, if
![]() $S\subseteq S'$
, then
$S\subseteq S'$
, then
![]() $R_{S'}$
is a congruence containing
$R_{S'}$
is a congruence containing
![]() $\{1\}\times S'$
and consequently, also
$\{1\}\times S'$
and consequently, also
![]() $\{1\}\times S$
so that
$\{1\}\times S$
so that
![]() $R_S\subseteq R_{S'}$
by definition of
$R_S\subseteq R_{S'}$
by definition of
![]() $R_S$
. Since
$R_S$
. Since
![]() $S,S'\subseteq S\vee S'$
, it follows that
$S,S'\subseteq S\vee S'$
, it follows that
![]() $R_S,R_{S'}\subseteq R_{S\vee S'}$
and hence,
$R_S,R_{S'}\subseteq R_{S\vee S'}$
and hence,
![]() $R_S\vee R_{S'}\subseteq R_{S\vee S'}$
by definition of the join
$R_S\vee R_{S'}\subseteq R_{S\vee S'}$
by definition of the join
![]() $R_S\vee R_{S'}$
. To prove the reverse inclusion, it is enough to observe that for all normal submonoids
$R_S\vee R_{S'}$
. To prove the reverse inclusion, it is enough to observe that for all normal submonoids
![]() $S,S'$
, the equivalence class of the identity element modulo
$S,S'$
, the equivalence class of the identity element modulo
![]() $R_S\vee R_{S'}$
is a normal submonoid that contains both S and
$R_S\vee R_{S'}$
is a normal submonoid that contains both S and
![]() $S'$
and hence, also
$S'$
and hence, also
![]() $S\vee S'$
. Therefore,
$S\vee S'$
. Therefore,
![]() $R_{S\vee S'}\subseteq R_S\vee R_{S'}$
by definition of
$R_{S\vee S'}\subseteq R_S\vee R_{S'}$
by definition of
![]() $R_{S\vee S'}$
. This proves that
$R_{S\vee S'}$
. This proves that
![]() $\Phi _M$
is join-preserving. As for
$\Phi _M$
is join-preserving. As for
![]() $\Psi _M$
, it is clearly order-preserving, and for all congruences
$\Psi _M$
, it is clearly order-preserving, and for all congruences
![]() $R,R'$
, and every
$R,R'$
, and every
![]() $x\in M$
, we have
$x\in M$
, we have
![]() $[x]_{R\cap R'}=[x]_R\cap [x]_{R'}$
. In particular, this is true when
$[x]_{R\cap R'}=[x]_R\cap [x]_{R'}$
. In particular, this is true when
![]() $x=1$
, that is,
$x=1$
, that is,
![]() $\Psi _M$
is meet-preserving. This proves item (a).
$\Psi _M$
is meet-preserving. This proves item (a).
To prove item (b), we have to see that
![]() $[1]_{R_S}=S$
for every normal submonoid S of M. The inclusion
$[1]_{R_S}=S$
for every normal submonoid S of M. The inclusion
![]() $S\subseteq \,[1]_{R_S}$
follows from the definition of
$S\subseteq \,[1]_{R_S}$
follows from the definition of
![]() $R_S$
. To prove the reverse inclusion, let us consider an element
$R_S$
. To prove the reverse inclusion, let us consider an element
![]() $z\in [1]_{R_S}$
. By the previous description of
$z\in [1]_{R_S}$
. By the previous description of
![]() $R_S$
, this means that there exists a finite sequence
$R_S$
, this means that there exists a finite sequence
![]() $x_0,\ldots ,x_k$
of elements in M such that
$x_0,\ldots ,x_k$
of elements in M such that
![]() $x_0=1$
,
$x_0=1$
,
![]() $x_k=z$
, and either
$x_k=z$
, and either
![]() $x_i\underset {S}{\rightsquigarrow} x_{i+1}$
or
$x_i\underset {S}{\rightsquigarrow} x_{i+1}$
or
![]() $x_{i+1}\underset {S}{\rightsquigarrow} x_i$
for each
$x_{i+1}\underset {S}{\rightsquigarrow} x_i$
for each
![]() $i\in \{0,1,\ldots ,k-1\}$
. Then to see that
$i\in \{0,1,\ldots ,k-1\}$
. Then to see that
![]() $z\in S$
, we prove the following facts:
$z\in S$
, we prove the following facts:
-
(i) every elementary S-deformation of an element in S is again an element in S; and
-
(ii) an element in S can be an elementary S-deformation of an element
 $v\in M$
only if
$v\in M$
only if
 $v\in S$
.
$v\in S$
.
Clearly, if both of these facts are true, every element in the above sequence
![]() $x_0,\ldots ,x_k$
is in S because
$x_0,\ldots ,x_k$
is in S because
![]() $x_0=1\in S$
. In particular, we have
$x_0=1\in S$
. In particular, we have
![]() $z=x_k\in S$
and hence,
$z=x_k\in S$
and hence,
![]() $[1]_{R_S}\subseteq S$
. Let us prove items (i) and (ii).
$[1]_{R_S}\subseteq S$
. Let us prove items (i) and (ii).
Proof of item (i). Let
![]() $w\in M$
be an S-deformation of some element
$w\in M$
be an S-deformation of some element
![]() $s\in S$
. This means that there exist
$s\in S$
. This means that there exist
![]() $x,y\in M$
, and
$x,y\in M$
, and
![]() $s'\in S$
such that
$s'\in S$
such that
![]() $s=xy$
, and
$s=xy$
, and
![]() $w=xs'y$
. However,
$w=xs'y$
. However,
![]() $s=xy\in S$
implies that
$s=xy\in S$
implies that
![]() $w=xs'y\in xSy\subseteq S$
because of the invariance of S.
$w=xs'y\in xSy\subseteq S$
because of the invariance of S.
Proof of item (ii). Let
![]() $s\in S$
be an elementary S-deformation of
$s\in S$
be an elementary S-deformation of
![]() $v\in M$
. This means that there exist
$v\in M$
. This means that there exist
![]() $v_1,v_2\in M$
and
$v_1,v_2\in M$
and
![]() $s'\in S$
such that
$s'\in S$
such that
![]() $v=v_1v_2$
and
$v=v_1v_2$
and
![]() $s=v_1s'v_2$
. In particular, we have
$s=v_1s'v_2$
. In particular, we have
![]() $s\in (v_1Sv_2)\cap S$
and hence,
$s\in (v_1Sv_2)\cap S$
and hence,
![]() $v=v_1v_2\in S$
because of the invariance of S.
$v=v_1v_2\in S$
because of the invariance of S.
Corollary 3.7. Let
![]() $A,B$
be subsets of M. Then:
$A,B$
be subsets of M. Then:
-
(a)
 $R_A=R_{B}$
if and only if
$R_A=R_{B}$
if and only if
 $\mathrm {ncl}_M(A)=\mathrm {ncl}_M(B)$
;
$\mathrm {ncl}_M(A)=\mathrm {ncl}_M(B)$
; -
(b)
 $[1]_{R_A}=\mathrm {ncl}_M(A)$
.
$[1]_{R_A}=\mathrm {ncl}_M(A)$
.
The next corollary mimics the fact that every normal subgroup of a group G is the kernel of some group homomorphism with domain G, thus providing more arguments in favor of the idea that normal submonoids are the right analog for arbitrary monoids of the normal subgroups of a group.
Corollary 3.8. Let M be a monoid. Then every normal submonoid S of M is the preimage
![]() $f^{-1}(1)$
of a monoid homomorphism
$f^{-1}(1)$
of a monoid homomorphism
![]() $f:M\to N$
for some monoid N.
$f:M\to N$
for some monoid N.
Proof. It follows from Theorem 3.6 that S is the preimage of the identity element by the projection of M onto its quotient
![]() $M/R_S$
.
$M/R_S$
.
With additional assumptions on M, it is possible to go further. For instance, if M is a cancellative commutative monoid satisfying condition (*) of Theorem 2.27, then we have the following stronger result.
Proposition 3.9. Let M be a cancellative commutative monoid satisfying condition (*) of Theorem 2.27. Then
![]() $\mathsf {NorSub}(M)$
embeds isomorphically onto a sublattice of
$\mathsf {NorSub}(M)$
embeds isomorphically onto a sublattice of
![]() $\mathsf {Cong}(M)$
.
$\mathsf {Cong}(M)$
.
Proof. It is enough to see that
![]() $\Phi _M$
is also meet-preserving when M is as in the statement. For all normal submonoids
$\Phi _M$
is also meet-preserving when M is as in the statement. For all normal submonoids
![]() $S,S'$
of any monoid M, we always have
$S,S'$
of any monoid M, we always have
![]() $R_{S\cap S'}\subseteq R_S\cap R_{S'}$
because
$R_{S\cap S'}\subseteq R_S\cap R_{S'}$
because
![]() $R_S\cap R_{S'}$
is a congruence containing
$R_S\cap R_{S'}$
is a congruence containing
![]() $\{1\}\times (S\cap S')$
. Conversely, let us assume that
$\{1\}\times (S\cap S')$
. Conversely, let us assume that
![]() $(x,y)\in R_S\cap R_{S'}$
. Since M is commutative, this means that there exist
$(x,y)\in R_S\cap R_{S'}$
. Since M is commutative, this means that there exist
![]() $s_1,s_2\in S$
and
$s_1,s_2\in S$
and
![]() $s^{\prime }_1,s^{\prime }_2\in S'$
such that
$s^{\prime }_1,s^{\prime }_2\in S'$
such that
![]() $x+s_1=y+s_2$
and
$x+s_1=y+s_2$
and
![]() $x+s^{\prime }_1=y+s^{\prime }_2$
. Hence,
$x+s^{\prime }_1=y+s^{\prime }_2$
. Hence,
and consequently,
![]() $s_1+s^{\prime }_2=s^{\prime }_1+s_2$
because M is cancellative. Let us now observe that if M satisfies condition (*), then every normal submonoid of M also satisfies condition (*). Indeed, if
$s_1+s^{\prime }_2=s^{\prime }_1+s_2$
because M is cancellative. Let us now observe that if M satisfies condition (*), then every normal submonoid of M also satisfies condition (*). Indeed, if
![]() $s_1, s_2\in S$
, with
$s_1, s_2\in S$
, with
![]() $S\lhd M$
, are such that
$S\lhd M$
, are such that
![]() $s_2=s_1+z$
for some
$s_2=s_1+z$
for some
![]() $z\in M$
, then
$z\in M$
, then
![]() $z\in LX_S$
and hence,
$z\in LX_S$
and hence,
![]() $z=z+0\in S$
. Then we may assume that
$z=z+0\in S$
. Then we may assume that
![]() $s^{\prime }_2=s^{\prime }_1+s'$
for some
$s^{\prime }_2=s^{\prime }_1+s'$
for some
![]() $s'\in S'$
. Then,
$s'\in S'$
. Then,
and hence,
![]() $s_2=s_1+s'$
, that is,
$s_2=s_1+s'$
, that is,
![]() $s'\in LX_S$
. Since S is invariant, it follows that
$s'\in LX_S$
. Since S is invariant, it follows that
![]() $s'\in S$
and consequently,
$s'\in S$
and consequently,
![]() $s'\in S\cap S'$
. Coming back to the initial hypothesis that
$s'\in S\cap S'$
. Coming back to the initial hypothesis that
![]() $x+s_1=y+s_2$
, we conclude that
$x+s_1=y+s_2$
, we conclude that
and hence
![]() $x=y+s'$
, that is,
$x=y+s'$
, that is,
![]() $(x,y)\in R_{S\cap S'}$
.
$(x,y)\in R_{S\cap S'}$
.
Remark 3.10. In general,
![]() $\Phi _M$
seems to be not meet-preserving. Although we always have
$\Phi _M$
seems to be not meet-preserving. Although we always have
![]() $R_{S\cap S'}\subseteq R_S\cap R_{S'}$
, it seems that the reverse inclusion can be false. In fact,
$R_{S\cap S'}\subseteq R_S\cap R_{S'}$
, it seems that the reverse inclusion can be false. In fact,
![]() $(x,y)\in R_S\cap R_{S'}$
if and only if
$(x,y)\in R_S\cap R_{S'}$
if and only if
![]() $x,y$
can be connected by both a finite sequence of elementary S-deformations and a finite sequence of elementary
$x,y$
can be connected by both a finite sequence of elementary S-deformations and a finite sequence of elementary
![]() $S'$
-deformations. However, it is not clear that this is enough for the existence of a finite sequence of elementary
$S'$
-deformations. However, it is not clear that this is enough for the existence of a finite sequence of elementary
![]() $(S\cap ~S')$
-deformations connecting them. Similarly, in general,
$(S\cap ~S')$
-deformations connecting them. Similarly, in general,
![]() $\Psi _M$
seems to be not join-preserving. We always have
$\Psi _M$
seems to be not join-preserving. We always have
![]() $[1]_R\vee [1]_{R'}\subseteq [1]_{R\vee R'}$
because
$[1]_R\vee [1]_{R'}\subseteq [1]_{R\vee R'}$
because
![]() $[1]_{R\vee R'}$
is a normal submonoid containing both
$[1]_{R\vee R'}$
is a normal submonoid containing both
![]() $[1]_R$
and
$[1]_R$
and
![]() $[1]_{R'}$
. However, in general, the converse
$[1]_{R'}$
. However, in general, the converse
![]() $[1]_{R\vee R'}\subseteq [1]_{R}\vee [1]_{R'}$
seems to be false.
$[1]_{R\vee R'}\subseteq [1]_{R}\vee [1]_{R'}$
seems to be false.
3.3 Normal and exceptional congruences
Although
![]() $\Phi _M$
is always injective, it is not surjective for a generic monoid. As shown by the examples mentioned in the introduction, for a given normal submonoid
$\Phi _M$
is always injective, it is not surjective for a generic monoid. As shown by the examples mentioned in the introduction, for a given normal submonoid
![]() $S\lhd M$
, the congruence
$S\lhd M$
, the congruence
![]() $R_S$
may be just one of several congruences on M having S as the equivalence class of the identity element. This suggests distinguishing the following two types of congruences on, and quotients of, a generic monoid.
$R_S$
may be just one of several congruences on M having S as the equivalence class of the identity element. This suggests distinguishing the following two types of congruences on, and quotients of, a generic monoid.
Definition 3.11. A congruence R on a monoid M is called normal if
![]() $R=R_S$
for some normal submonoid S of M (equivalently, if R is in the image of
$R=R_S$
for some normal submonoid S of M (equivalently, if R is in the image of
![]() $\Phi _M$
). Otherwise, it is called exceptional. Similarly, a quotient of M is called normal (respectively exceptional) when it is the quotient of M modulo a normal (respectively exceptional) congruence.
$\Phi _M$
). Otherwise, it is called exceptional. Similarly, a quotient of M is called normal (respectively exceptional) when it is the quotient of M modulo a normal (respectively exceptional) congruence.
Example 3.12. It follows from Proposition 2.9 that the nontrivial normal congruences in the additive monoid
![]() $\mathbb {N}_+$
are
$\mathbb {N}_+$
are
![]() $R_{0,n}=\{(i,j)\in \mathbb {N}\times \mathbb {N} : i\equiv j\ (\mbox {mod } n)\}$
for each
$R_{0,n}=\{(i,j)\in \mathbb {N}\times \mathbb {N} : i\equiv j\ (\mbox {mod } n)\}$
for each
![]() $n\geq 1$
, with
$n\geq 1$
, with
![]() $[0]=\langle n\rangle $
. Up to isomorphism, the corresponding normal quotients are the cyclic groups
$[0]=\langle n\rangle $
. Up to isomorphism, the corresponding normal quotients are the cyclic groups
![]() $(\mathbb {Z}_n,+,0)$
.
$(\mathbb {Z}_n,+,0)$
.
Let us denote by
![]() $\mathsf {NorCong}(M)$
the subset of
$\mathsf {NorCong}(M)$
the subset of
![]() $\mathsf {Cong}(M)$
consisting of the normal congruences on M ordered by inclusion. Then Theorem 3.6 can be restated as follows.
$\mathsf {Cong}(M)$
consisting of the normal congruences on M ordered by inclusion. Then Theorem 3.6 can be restated as follows.
Corollary 3.13. For every monoid M,
![]() $\mathsf {NorCon}(M)$
is a complete lattice isomorphic to
$\mathsf {NorCon}(M)$
is a complete lattice isomorphic to
![]() $\mathsf {NorSub}(M)$
.
$\mathsf {NorSub}(M)$
.
Proof. It follows from Theorem 3.6 that the corestriction of
![]() $\Phi _M$
to
$\Phi _M$
to
![]() $\mathsf {NorCon}(M)$
is an order-preserving bijection from
$\mathsf {NorCon}(M)$
is an order-preserving bijection from
![]() $\mathsf {NorSub}(M)$
to
$\mathsf {NorSub}(M)$
to
![]() $\mathsf {NorCon}(M)$
whose inverse map is given by
$\mathsf {NorCon}(M)$
whose inverse map is given by
![]() $R\mapsto [1]_R$
and hence, also an order-preserving map.
$R\mapsto [1]_R$
and hence, also an order-preserving map.
Let us emphasize that
![]() $\mathsf {NorCon}(M)$
seems to be just a join subsemilattice of
$\mathsf {NorCon}(M)$
seems to be just a join subsemilattice of
![]() $\mathsf {Cong}(M)$
because the meet of two generic normal congruences
$\mathsf {Cong}(M)$
because the meet of two generic normal congruences
![]() $R_S,R_{S'}$
in
$R_S,R_{S'}$
in
![]() $\mathsf {NorCong}(M)$
is
$\mathsf {NorCong}(M)$
is
![]() $R_{S\cap S'}$
but not necessarily in
$R_{S\cap S'}$
but not necessarily in
![]() $\mathsf {Cong}(M)$
(compare with Remark 3.10 above).
$\mathsf {Cong}(M)$
(compare with Remark 3.10 above).
3.4 The set of congruences as a ‘blow up’ of the set of normal submonoids
For each normal submonoid S of M, let
Notice that
![]() $\mathsf {Cong}_S(M)\subseteq \mathsf {Cong}(M,S)$
, and that it contains the minimal element
$\mathsf {Cong}_S(M)\subseteq \mathsf {Cong}(M,S)$
, and that it contains the minimal element
![]() $R_S$
and unique normal congruence in
$R_S$
and unique normal congruence in
![]() $\mathsf {Cong}(M,S)$
. When
$\mathsf {Cong}(M,S)$
. When
![]() $S=\{1\}$
, we write
$S=\{1\}$
, we write
![]() $\mathsf {Cong}_1(M)$
(or
$\mathsf {Cong}_1(M)$
(or
![]() $\mathsf {Cong}_0(M)$
in the additive case) instead of
$\mathsf {Cong}_0(M)$
in the additive case) instead of
![]() $\mathsf {Cong}_{\{1\}}(M)$
. Its elements are the unital congruences on M mentioned in the introduction.
$\mathsf {Cong}_{\{1\}}(M)$
. Its elements are the unital congruences on M mentioned in the introduction.
When ordered by inclusion,
![]() $\mathsf {Cong}_S(M)$
is a meet subsemilattice of
$\mathsf {Cong}_S(M)$
is a meet subsemilattice of
![]() $\mathsf {Cong}(M,S)$
and hence, of
$\mathsf {Cong}(M,S)$
and hence, of
![]() $\mathsf {Cong}(M)$
. However, it is not a join subsemilattice in general. Thus, if
$\mathsf {Cong}(M)$
. However, it is not a join subsemilattice in general. Thus, if
![]() $R,R'\in \mathsf {Cong}_1(M)$
, then their join
$R,R'\in \mathsf {Cong}_1(M)$
, then their join
![]() $R\vee R'$
in
$R\vee R'$
in
![]() $\mathsf {Cong}(M,S)$
(and in
$\mathsf {Cong}(M,S)$
(and in
![]() $\mathsf {Cong}(M)$
) need not be a congruence in
$\mathsf {Cong}(M)$
) need not be a congruence in
![]() $\mathsf {Cong}_S(M)$
because we only have the inclusion
$\mathsf {Cong}_S(M)$
because we only have the inclusion
![]() $[1]_R\vee [1]_{R'}\subseteq [1]_{R\vee R'}$
.
$[1]_R\vee [1]_{R'}\subseteq [1]_{R\vee R'}$
.
It readily follows from Theorem 3.6 that, as a set,
![]() $\mathsf {Cong}(M)$
is in bijection with the ‘blow up’ of
$\mathsf {Cong}(M)$
is in bijection with the ‘blow up’ of
![]() $\mathsf {NorSub}(M)$
(equivalently, of
$\mathsf {NorSub}(M)$
(equivalently, of
![]() $\mathsf {NorCong}(M)$
; compare with Corollary 3.13) obtained when each normal submonoid S (normal congruence
$\mathsf {NorCong}(M)$
; compare with Corollary 3.13) obtained when each normal submonoid S (normal congruence
![]() $R_S$
) is replaced by the set
$R_S$
) is replaced by the set
![]() $\mathsf {Cong}_S(M)$
. It turns out that, up to isomorphism,
$\mathsf {Cong}_S(M)$
. It turns out that, up to isomorphism,
![]() $\mathsf {Cong}_S(M)$
is given by the set of unital congruences on the quotient monoid
$\mathsf {Cong}_S(M)$
is given by the set of unital congruences on the quotient monoid
![]() $M/R_S$
, or
$M/R_S$
, or
![]() $M/S$
for short. More precisely, the following holds true.
$M/S$
for short. More precisely, the following holds true.
Proposition 3.14. Let M be a monoid and
![]() $S\lhd M$
. Then
$S\lhd M$
. Then
![]() $\mathsf {Cong}_S(M)$
is isomorphic, as a meet semilattice, to
$\mathsf {Cong}_S(M)$
is isomorphic, as a meet semilattice, to
![]() $\mathsf {Cong}_1(M/S)$
. In particular,
$\mathsf {Cong}_1(M/S)$
. In particular,
![]() $R_S$
is mapped through the isomorphism to the trivial unital congruence on
$R_S$
is mapped through the isomorphism to the trivial unital congruence on
![]() $M/S$
.
$M/S$
.
Proof. Let us first observe that every congruence
![]() $R\in \mathsf {Cong}_S(M)$
induces a unital congruence on the quotient
$R\in \mathsf {Cong}_S(M)$
induces a unital congruence on the quotient
![]() $M/S$
given by
$M/S$
given by
Indeed, if
![]() $(x,y)\in R$
, and
$(x,y)\in R$
, and
![]() $x',y'\in M$
are such that
$x',y'\in M$
are such that
![]() $(x',x)\in R_S$
,
$(x',x)\in R_S$
,
![]() $(y,y')\in R_S$
, then we also have
$(y,y')\in R_S$
, then we also have
![]() $(x,x')\in R$
and
$(x,x')\in R$
and
![]() $(y,y')\in R$
because
$(y,y')\in R$
because
![]() $R_S$
is the minimum of
$R_S$
is the minimum of
![]() $\mathsf {Cong}_S(M)$
. By transitivity, it follows that
$\mathsf {Cong}_S(M)$
. By transitivity, it follows that
![]() $(x',y')\in R$
and hence,
$(x',y')\in R$
and hence,
![]() $\tilde {R}$
is a well-defined binary relation on
$\tilde {R}$
is a well-defined binary relation on
![]() $M/S$
. Moreover, it is immediate to check that
$M/S$
. Moreover, it is immediate to check that
![]() $\tilde {R}$
is a congruence because this is true for R. Finally,
$\tilde {R}$
is a congruence because this is true for R. Finally,
![]() $[x]_{R_S}\tilde {R}\,[1]_{R_S}$
means that
$[x]_{R_S}\tilde {R}\,[1]_{R_S}$
means that
![]() $x\,R\,1$
and hence,
$x\,R\,1$
and hence,
![]() $x\in [1]_{R}=S=[1]_{R_S}$
, that is,
$x\in [1]_{R}=S=[1]_{R_S}$
, that is,
![]() $\tilde {R}$
is unital. In particular, when R is
$\tilde {R}$
is unital. In particular, when R is
![]() $R_S$
, then
$R_S$
, then
![]() $\tilde {R}$
is the trivial congruence on
$\tilde {R}$
is the trivial congruence on
![]() $M/S$
. Conversely, every unital congruence T on
$M/S$
. Conversely, every unital congruence T on
![]() $M/S$
induces a congruence
$M/S$
induces a congruence
![]() $T^*$
on M given by
$T^*$
on M given by
and
![]() $T^*$
is such that
$T^*$
is such that
![]() $[1]_{T^*}=S$
. Indeed,
$[1]_{T^*}=S$
. Indeed,
![]() $[[1]_{R_S}]_T=\{[1]_{R_S}\}$
because T is unital. Hence, for each
$[[1]_{R_S}]_T=\{[1]_{R_S}\}$
because T is unital. Hence, for each
![]() $x\in M$
,
$x\in M$
,
Then it is easy to check that the maps
![]() $t_S:\mathsf {Cong}_S(M)\to \mathsf {Cong}_1(M/S)$
and
$t_S:\mathsf {Cong}_S(M)\to \mathsf {Cong}_1(M/S)$
and
![]() $t^*_S:\mathsf {Cong}_1(M/S)\to \mathsf {Cong}_S(M)$
respectively given by
$t^*_S:\mathsf {Cong}_1(M/S)\to \mathsf {Cong}_S(M)$
respectively given by
![]() $R\mapsto \tilde {R}$
, and
$R\mapsto \tilde {R}$
, and
![]() $T\mapsto T^*$
are inverses of each other. Moreover, both are order-preserving and hence, they define a meet semilattice isomorphism.
$T\mapsto T^*$
are inverses of each other. Moreover, both are order-preserving and hence, they define a meet semilattice isomorphism.
This result, together with Theorem 3.6, leads to the following description of the set of congruences on an arbitrary monoid.
Theorem 3.15. For every monoid M, there is a (set-theoretic) bijection
 $$ \begin{align} \mathsf{Cong}(M)\longrightarrow\bigcup_{S\in\mathsf{NorSub}(M)}\mathsf{Cong}_1(M/S) \end{align} $$
$$ \begin{align} \mathsf{Cong}(M)\longrightarrow\bigcup_{S\in\mathsf{NorSub}(M)}\mathsf{Cong}_1(M/S) \end{align} $$
given by
![]() $R\mapsto t_{[1]_R}(R)$
, and whose inverse is given by
$R\mapsto t_{[1]_R}(R)$
, and whose inverse is given by
![]() $T\mapsto t^*_S(T)$
for each
$T\mapsto t^*_S(T)$
for each
![]() $T\in \mathsf {Cong}_1(M/S)$
. Moreover, the exceptional congruences on M are mapped through this bijection to the nontrivial unital congruences on the normal quotients of M.
$T\in \mathsf {Cong}_1(M/S)$
. Moreover, the exceptional congruences on M are mapped through this bijection to the nontrivial unital congruences on the normal quotients of M.
This theorem reduces the computation of the whole set of congruences on an arbitrary monoid M to the computation of:
-
(1) its set
 $\mathsf {NorSub}(M)$
of normal submonoids (equivalently, normal congruences);
$\mathsf {NorSub}(M)$
of normal submonoids (equivalently, normal congruences); -
(2) the normal quotient
 $M/S$
for each normal submonoid S of M; and
$M/S$
for each normal submonoid S of M; and -
(3) the set
 $\mathsf {Cong}_1(M/S)$
of unital congruences on each normal quotient
$\mathsf {Cong}_1(M/S)$
of unital congruences on each normal quotient
 $M/S$
.
$M/S$
.
As it becomes clear from the bijection in Equation (3-1), the higher complexity of the theory of congruences on generic monoids with respect to the corresponding theory for groups ultimately comes from the existence of nontrivial unital congruences on a monoid. For every group G, there is only one unital congruence on G, so that every term in the right-hand side of Equation (3-1) is a singleton. In fact, the following characterizations of the unital congruences on a generic monoid are straightforward.
Proposition 3.16. Let R be a congruence on a monoid M. Then the following are equivalent:
-
(i) R is unital;
-
(ii) for each
 $x,y\in M$
, if
$x,y\in M$
, if
 $(x,y)\in R$
and
$(x,y)\in R$
and
 $x\in U(M)$
, then
$x\in U(M)$
, then
 $x=y$
;
$x=y$
; -
(iii) the restriction of R to the group of units
 $U(M)$
is the identity relation
$U(M)$
is the identity relation
 $\Delta _{U(M)}$
.
$\Delta _{U(M)}$
.
Proof. Let R be unital, so that
![]() [1]_R=\{1\}
, and let
[1]_R=\{1\}
, and let
![]() $x,y\in M$
such
$x,y\in M$
such
![]() $x\in U(M)$
, and
$x\in U(M)$
, and
![]() $(x,y)\in R$
. Then
$(x,y)\in R$
. Then
![]() $(1,x^{-1}y),(1,yx^{-1})\in R$
and hence,
$(1,x^{-1}y),(1,yx^{-1})\in R$
and hence,
![]() $x^{-1}y=yx^{-1}=1$
, that is
$x^{-1}y=yx^{-1}=1$
, that is
![]() $x=y$
. This proves that (i) implies (ii). The remaining implications (ii)
$x=y$
. This proves that (i) implies (ii). The remaining implications (ii)
![]() $\Rightarrow $
(iii), and (iii)
$\Rightarrow $
(iii), and (iii)
![]() $\Rightarrow $
(i) are immediate.
$\Rightarrow $
(i) are immediate.
3.5 Congruentially simple monoids
As pointed out before, the exceptional congruences on a monoid M are in bijection with the nontrivial unital congruences on its normal quotients. This suggests introducing the following definition.
Definition 3.17. A monoid M is called congruentially simple if its only normal quotient having nontrivial unital congruences is the monoid M as normal quotient of itself.
For such monoids, the equivalence class of the identity element is trivial in all exceptional congruences, and for every normal submonoid
![]() $S\neq \{1\}$
, there is a unique congruence R such that
$S\neq \{1\}$
, there is a unique congruence R such that
![]() $[1]_R=S$
. In other words, a monoid is congruentially simple if all its congruences are uniquely determined by the equivalence class of the identity element except when this class is trivial. Once more, the question arises whether every monoid is congruentially simple, and if it is not, to identify families of monoids that are congruentially simple.
$[1]_R=S$
. In other words, a monoid is congruentially simple if all its congruences are uniquely determined by the equivalence class of the identity element except when this class is trivial. Once more, the question arises whether every monoid is congruentially simple, and if it is not, to identify families of monoids that are congruentially simple.
Example 3.18.
![]() $\mathbb {N}_+$
is congruentially simple. Indeed, it follows from Proposition 2.9 and Example 3.1 that, up to isomorphism, the only nontrivial, proper normal quotients of
$\mathbb {N}_+$
is congruentially simple. Indeed, it follows from Proposition 2.9 and Example 3.1 that, up to isomorphism, the only nontrivial, proper normal quotients of
![]() $\mathbb {N}_+$
are the additive groups
$\mathbb {N}_+$
are the additive groups
![]() $\mathbb {Z}_n$
for each
$\mathbb {Z}_n$
for each
![]() $n\geq 2$
. As they are all groups, there are no nontrivial unital congruences on them. Hence,
$n\geq 2$
. As they are all groups, there are no nontrivial unital congruences on them. Hence,
![]() $\mathsf {Cong}(\mathbb {N}_+)$
consists of the normal congruences
$\mathsf {Cong}(\mathbb {N}_+)$
consists of the normal congruences
![]() $\Delta _{\mathbb {N}}$
and
$\Delta _{\mathbb {N}}$
and
![]() $R_{0,n}$
for each
$R_{0,n}$
for each
![]() $n\geq 1$
, together with the nontrivial unital congruences on
$n\geq 1$
, together with the nontrivial unital congruences on
![]() $\mathbb {N}_+$
.
$\mathbb {N}_+$
.
As discussed in the next subsection, the finite full transformation monoids
![]() $T_n$
are also congruentially simple.
$T_n$
are also congruentially simple.
3.6 Malcev’s theorem revisited
In a now classical paper from 1952, Malcev computed the lattice of congruences of the finite full transformation monoids
![]() $T_n$
,
$T_n$
,
![]() $n\geq 1$
[Reference Malcev10]. The computation starts with the fact that the lattice of ideals of
$n\geq 1$
[Reference Malcev10]. The computation starts with the fact that the lattice of ideals of
![]() $T_n$
is given by the chain
$T_n$
is given by the chain
where
![]() $I_k$
stands for the set of endomorphisms of
$I_k$
stands for the set of endomorphisms of
![]() $\mathbf {n}:=\{1,\ldots ,n\}$
of rank
$\mathbf {n}:=\{1,\ldots ,n\}$
of rank
![]() $\leq k$
(by the rank of such an endomorphism, it is meant the cardinal of its image). Malcev realized that for every congruence R on
$\leq k$
(by the rank of such an endomorphism, it is meant the cardinal of its image). Malcev realized that for every congruence R on
![]() $T_n$
different from the uniform congruence
$T_n$
different from the uniform congruence
![]() $\nabla _{T_n}:=T_n\times T_n$
, there is some
$\nabla _{T_n}:=T_n\times T_n$
, there is some
![]() $k\in \{1,\ldots ,n\}$
and some normal subgrup
$k\in \{1,\ldots ,n\}$
and some normal subgrup
![]() $N\lhd S_k$
such that R is the identity on
$N\lhd S_k$
such that R is the identity on
![]() $I_n\setminus I_k$
, it identifies all endomorphisms in
$I_n\setminus I_k$
, it identifies all endomorphisms in
![]() $I_{k-1}$
, and its restriction to
$I_{k-1}$
, and its restriction to
![]() $I_k\setminus I_{k-1}$
is completely given by N. To be precise, two endomorphisms
$I_k\setminus I_{k-1}$
is completely given by N. To be precise, two endomorphisms
![]() $u,v\in I_k\setminus I_{k-1}$
are equivalent if and only if
$u,v\in I_k\setminus I_{k-1}$
are equivalent if and only if
![]() $u=v$
or the following three conditions hold:
$u=v$
or the following three conditions hold:
-
(1) both have the same image
 $\{i_1,\ldots ,i_k\}\subseteq \mathbf {n}$
;
$\{i_1,\ldots ,i_k\}\subseteq \mathbf {n}$
; -
(2)
 $u^{-1}(i_j)=v^{-1}(i_j)$
for each
$u^{-1}(i_j)=v^{-1}(i_j)$
for each
 $j=1,\ldots ,k$
; and
$j=1,\ldots ,k$
; and -
(3) there exists a permutation
 $\tau \in N$
such that
$\tau \in N$
such that
 $v=\tau u$
.
$v=\tau u$
.
Let
![]() $R_{k,N}$
be the congruence so defined by the pair
$R_{k,N}$
be the congruence so defined by the pair
![]() $(k,N)$
. For instance,
$(k,N)$
. For instance,
![]() $R_{1,S_1}$
is the identity congruence
$R_{1,S_1}$
is the identity congruence
![]() $\Delta _{T_n}$
and
$\Delta _{T_n}$
and
![]() $R_{k,\{1\}}$
for any
$R_{k,\{1\}}$
for any
![]() $k\geq 2$
is the Rees congruence
$k\geq 2$
is the Rees congruence
![]() $R_{I_{k-1}}$
mentioned in the introduction. Clearly, if
$R_{I_{k-1}}$
mentioned in the introduction. Clearly, if
![]() $k\leq k'$
, then
$k\leq k'$
, then
![]() $R_{k,N}\subseteq R_{k',N'}$
for every normal subgroups
$R_{k,N}\subseteq R_{k',N'}$
for every normal subgroups
![]() $N\lhd S_k$
, and
$N\lhd S_k$
, and
![]() $N'\lhd S_{k'}$
with
$N'\lhd S_{k'}$
with
![]() $N\subseteq N'$
when
$N\subseteq N'$
when
![]() $k=k'$
. It follows that the whole lattice of congruences on
$k=k'$
. It follows that the whole lattice of congruences on
![]() $T_n$
is given by the chain
$T_n$
is given by the chain
 $$ \begin{align*} &\mbox{if } n=2{:}\ \ \Delta_{T_2}\subseteq R_{I_1}\subseteq R_{2,S_2}\subseteq\nabla_{T_2} , \\ &\mbox{if } n=3{:}\ \ \Delta_{T_3}\subseteq R_{I_1}\subseteq R_{2,S_2}\subseteq R_{I_2}\subseteq R_{3,A_3}\subseteq R_{3,S_3}\subseteq\nabla_{T_3}, \\ &\mbox{if } n=4{:}\ \ \Delta_{T_4}\subseteq R_{I_1}\subseteq R_{2,S_2}\subseteq R_{I_2}\subseteq R_{3,A_3}\subseteq R_{3,S_3}\subseteq R_{I_3}\subseteq R_{4,K_4}\subseteq R_{4,A_4}\subseteq R_{4,S_4}\subseteq\nabla_{T_4}, \end{align*} $$
$$ \begin{align*} &\mbox{if } n=2{:}\ \ \Delta_{T_2}\subseteq R_{I_1}\subseteq R_{2,S_2}\subseteq\nabla_{T_2} , \\ &\mbox{if } n=3{:}\ \ \Delta_{T_3}\subseteq R_{I_1}\subseteq R_{2,S_2}\subseteq R_{I_2}\subseteq R_{3,A_3}\subseteq R_{3,S_3}\subseteq\nabla_{T_3}, \\ &\mbox{if } n=4{:}\ \ \Delta_{T_4}\subseteq R_{I_1}\subseteq R_{2,S_2}\subseteq R_{I_2}\subseteq R_{3,A_3}\subseteq R_{3,S_3}\subseteq R_{I_3}\subseteq R_{4,K_4}\subseteq R_{4,A_4}\subseteq R_{4,S_4}\subseteq\nabla_{T_4}, \end{align*} $$
and by the chain
 $$ \begin{align*} \Delta_{T_n}\subseteq R_{I_1}\subseteq R_{2,S_2}&\subseteq R_{I_2}\subseteq R_{3,A_3}\subseteq R_{3,S_3}\subseteq R_{I_3} \nonumber \\ &\subseteq R_{4,K_4}\subseteq R_{4,A_4}\subseteq R_{4,S_4}\subseteq \cdots\subseteq R_{I_{n-1}}\subseteq R_{n,A_n}\subseteq R_{n,S_n}\subseteq\nabla_{T_n} \end{align*} $$
$$ \begin{align*} \Delta_{T_n}\subseteq R_{I_1}\subseteq R_{2,S_2}&\subseteq R_{I_2}\subseteq R_{3,A_3}\subseteq R_{3,S_3}\subseteq R_{I_3} \nonumber \\ &\subseteq R_{4,K_4}\subseteq R_{4,A_4}\subseteq R_{4,S_4}\subseteq \cdots\subseteq R_{I_{n-1}}\subseteq R_{n,A_n}\subseteq R_{n,S_n}\subseteq\nabla_{T_n} \end{align*} $$
for each
![]() $n\geq 5$
, where
$n\geq 5$
, where
![]() $K_4$
denotes the Klein four-group; see [Reference Ganyushkin and Mazorchuk7] for a modern presentation of the subject, including the computation of the lattice of congruences of the related monoids
$K_4$
denotes the Klein four-group; see [Reference Ganyushkin and Mazorchuk7] for a modern presentation of the subject, including the computation of the lattice of congruences of the related monoids
![]() $PT_n$
of partial transformations and
$PT_n$
of partial transformations and
![]() $IS_n$
of partial injective transformations. Notice that the equivalence class of the identity element in
$IS_n$
of partial injective transformations. Notice that the equivalence class of the identity element in
![]() $R_{k,N}$
is
$R_{k,N}$
is
 $$ \begin{align*} [1]_{R_{k,N}}= \begin{cases} \{1\} & \mbox{if } k<n, \\ N & \mbox{if } k=n. \end{cases} \end{align*} $$
$$ \begin{align*} [1]_{R_{k,N}}= \begin{cases} \{1\} & \mbox{if } k<n, \\ N & \mbox{if } k=n. \end{cases} \end{align*} $$
Hence, the normal congruences on
![]() $T_n$
are the congruences
$T_n$
are the congruences
![]() $\Delta _{T_n}$
,
$\Delta _{T_n}$
,
![]() $R_{n,A_n}$
,
$R_{n,A_n}$
,
![]() $R_{n,S_n}$
, and
$R_{n,S_n}$
, and
![]() $\nabla _{T_n}$
(and
$\nabla _{T_n}$
(and
![]() $R_{4,K_4}$
when
$R_{4,K_4}$
when
![]() $n=4$
), and all exceptional congruences are in this case unital, that is,
$n=4$
), and all exceptional congruences are in this case unital, that is,
![]() $T_n$
is congruentially simple.
$T_n$
is congruentially simple.
Subsequent works devoted to the computation of the lattice of congruences on other specific families of monoids often follow the Malcev strategy, starting with the lattice of ideals of the monoid or, more precisely, with some ascending chain of ideals whose union is the whole monoid; see, in particular, the works by East and Ruskuc [Reference East and Ruskuc2–Reference East and Ruskuc5]. However, it is also possible to address the problem using Theorem 3.15. Although, at some point, we may be forced to converge to a strategy similar to Malcev’s, in particular, in the computation of the lattice of unital congruences of the normal quotients, this theorem offers a new strategy whose starting point is the lattice of normal submonoids, and this new strategy may allow us to achieve some results in a different way. This is the case of the congruential simplicity of
![]() $T_n$
, which can be proved directly without using the Malcev result.
$T_n$
, which can be proved directly without using the Malcev result.
Indeed, let us consider the generic case
![]() $n\geq 5$
. We know from Theorem 3.15 that the exceptional congruences on
$n\geq 5$
. We know from Theorem 3.15 that the exceptional congruences on
![]() $T_n$
are in bijection with the nontrivial unital congruences on the normal quotients of
$T_n$
are in bijection with the nontrivial unital congruences on the normal quotients of
![]() $T_n$
. Hence, a path to identify them consists of first computing all normal quotients and then looking for the unital congruences on each of these quotients.
$T_n$
. Hence, a path to identify them consists of first computing all normal quotients and then looking for the unital congruences on each of these quotients.
Proposition 3.19. Up to isomorphism, the nontrivial, proper normal quotients of
![]() $T_n$
for
$T_n$
for
![]() $n\geq 5$
are the multiplicative monoids
$n\geq 5$
are the multiplicative monoids
![]() $\{0,1\}$
and
$\{0,1\}$
and
![]() $\{-1,0,1\}$
.
$\{-1,0,1\}$
.
Proof. It follows from Example 2.24 that the only nontrivial, proper normal quotients of
![]() $T_n$
for
$T_n$
for
![]() $n\geq 5$
are
$n\geq 5$
are
![]() $T_n/S_n$
and
$T_n/S_n$
and
![]() $T_n/A_n$
. Hence, it is enough to prove that:
$T_n/A_n$
. Hence, it is enough to prove that:
-
(a)
 $T_n/S_n\cong (\{0,1\},\cdot ,1)$
;
$T_n/S_n\cong (\{0,1\},\cdot ,1)$
; -
(b)
 $T_n/A_n\cong (\{-1,0,1\},\cdot ,1)$
.
$T_n/A_n\cong (\{-1,0,1\},\cdot ,1)$
.
Proof of item (a). Recall that
![]() $T_n/S_n$
means the quotient of
$T_n/S_n$
means the quotient of
![]() $T_n$
modulo the smallest congruence
$T_n$
modulo the smallest congruence
![]() $R=R_{S_n}$
on
$R=R_{S_n}$
on
![]() $T_n$
such that
$T_n$
such that
![]() $[1]_{R}=S_n$
. In particular, for each
$[1]_{R}=S_n$
. In particular, for each
![]() $u\in S_n$
, we have
$u\in S_n$
, we have
![]() $[u]_R=S_n$
. It turns out that
$[u]_R=S_n$
. It turns out that
![]() $[u]_R=T_n\setminus S_n$
if
$[u]_R=T_n\setminus S_n$
if
![]() $u\notin S_n$
. To be precise, if
$u\notin S_n$
. To be precise, if
![]() $c_1:\mathbf {n}\to \mathbf {n}$
denotes the constant map defined by
$c_1:\mathbf {n}\to \mathbf {n}$
denotes the constant map defined by
![]() $c_1(k)=1$
for each
$c_1(k)=1$
for each
![]() $k\in \mathbf {n}$
, let us prove that
$k\in \mathbf {n}$
, let us prove that
The implication to the right is an immediate consequence of the fact that
![]() $[1]_R=S_n$
. Thus, if
$[1]_R=S_n$
. Thus, if
![]() $(u,c_1)\in R$
for some
$(u,c_1)\in R$
for some
![]() $u\in S_n$
, then we also have
$u\in S_n$
, then we also have
![]() $(1,c_1)\in R$
and hence,
$(1,c_1)\in R$
and hence,
![]() $c_1\in [1]_R=S_n$
which is clearly false. To prove the converse, we proceed by induction on the rank
$c_1\in [1]_R=S_n$
which is clearly false. To prove the converse, we proceed by induction on the rank
![]() $r\in \{1,\ldots ,n-1\}$
of u (that is, on the cardinality of its image). If
$r\in \{1,\ldots ,n-1\}$
of u (that is, on the cardinality of its image). If
![]() $r=1$
, then u is the constant map
$r=1$
, then u is the constant map
![]() $c_i$
sending every
$c_i$
sending every
![]() $k\in \mathbf {n}$
to i for some
$k\in \mathbf {n}$
to i for some
![]() $i\in \mathbf {n}$
, and
$i\in \mathbf {n}$
, and
![]() $c_1$
is clearly an elementary
$c_1$
is clearly an elementary
![]() $S_n$
-deformation of
$S_n$
-deformation of
![]() $c_i$
. Indeed,
$c_i$
. Indeed,
![]() $c_1$
is the composite of
$c_1$
is the composite of
![]() $c_i$
with the transposition
$c_i$
with the transposition
![]() $(1i)\in S_n$
. Hence,
$(1i)\in S_n$
. Hence,
![]() $(u,c_1)\in R$
. Let us now assume that for some
$(u,c_1)\in R$
. Let us now assume that for some
![]() $r\in \{1,\ldots ,n-2\}$
, every map of rank r is R-related to
$r\in \{1,\ldots ,n-2\}$
, every map of rank r is R-related to
![]() $c_1$
, and let u be of rank
$c_1$
, and let u be of rank
![]() $r+1$
. Since
$r+1$
. Since
![]() $r<n-1$
, we still have
$r<n-1$
, we still have
![]() $r+1<n$
and hence, there exists some
$r+1<n$
and hence, there exists some
![]() $i\in \mathbf {n}$
not in the image of u. Let j be any element in the image of u and l such that
$i\in \mathbf {n}$
not in the image of u. Let j be any element in the image of u and l such that
![]() $u(l)\neq j$
. Such an l exists because u is of rank
$u(l)\neq j$
. Such an l exists because u is of rank
![]() $r+1\geq 2$
. Then let us consider the map
$r+1\geq 2$
. Then let us consider the map
![]() $u':\mathbf {n}\to \mathbf {n}$
defined by
$u':\mathbf {n}\to \mathbf {n}$
defined by
 $$ \begin{align*} u'(k)=\begin{cases} k & \mbox{if } k\neq i, \\ j & \mbox{if } k=i. \end{cases} \end{align*} $$
$$ \begin{align*} u'(k)=\begin{cases} k & \mbox{if } k\neq i, \\ j & \mbox{if } k=i. \end{cases} \end{align*} $$
Clearly, we have
![]() $u'u=u$
. Hence, the composite
$u'u=u$
. Hence, the composite
![]() $\hat {u}=u'\tau u$
, with
$\hat {u}=u'\tau u$
, with
![]() $\tau $
the transposition
$\tau $
the transposition
![]() $(iu(l))\in S_n$
is an elementary
$(iu(l))\in S_n$
is an elementary
![]() $S_n$
-deformation of u and consequently,
$S_n$
-deformation of u and consequently,
![]() $(u,\hat {u})\in R$
. However,
$(u,\hat {u})\in R$
. However,
![]() $\hat {u}$
is of rank r because all elements in
$\hat {u}$
is of rank r because all elements in
![]() $u^{-1}(u(l))$
are now mapped not to
$u^{-1}(u(l))$
are now mapped not to
![]() $u(l)\neq j$
but to j, while
$u(l)\neq j$
but to j, while
![]() $\hat {u}(k)=u(k)$
for each
$\hat {u}(k)=u(k)$
for each
![]() $k\notin u^{-1}(u(l))$
. By the induction hypothesis,
$k\notin u^{-1}(u(l))$
. By the induction hypothesis,
![]() $(\hat {u},c_1)\in R$
and hence,
$(\hat {u},c_1)\in R$
and hence,
![]() $(u,c_1)\in R$
by transitivity. This proves Equation (3-2).
$(u,c_1)\in R$
by transitivity. This proves Equation (3-2).
It follows that the map
![]() $T_n\to \{0,1\}$
sending each
$T_n\to \{0,1\}$
sending each
![]() $u\notin S_n$
to
$u\notin S_n$
to
![]() $0$
and each
$0$
and each
![]() $u\in S_n$
to
$u\in S_n$
to
![]() $1$
is a monoid epimorphism that factors through the quotient
$1$
is a monoid epimorphism that factors through the quotient
![]() $T_n/S_n$
, and the induced map
$T_n/S_n$
, and the induced map
![]() $T_n/S_n\to \{0,1\}$
is a monoid isomorphism.
$T_n/S_n\to \{0,1\}$
is a monoid isomorphism.
Proof of item (b). Here,
![]() $T_n/A_n$
means the quotient of
$T_n/A_n$
means the quotient of
![]() $T_n$
modulo the smallest congruence
$T_n$
modulo the smallest congruence
![]() $R=R_{A_n}$
on
$R=R_{A_n}$
on
![]() $T_n$
such that
$T_n$
such that
![]() $[1]_{R}=A_n$
. In particular, for each
$[1]_{R}=A_n$
. In particular, for each
![]() $u\in A_n$
, we have
$u\in A_n$
, we have
![]() $[u]_R=A_n$
. It turns out now that
$[u]_R=A_n$
. It turns out now that
![]() $[u]_R=S_n\setminus A_n$
if
$[u]_R=S_n\setminus A_n$
if
![]() $u\in S_n\setminus A_n$
and
$u\in S_n\setminus A_n$
and
![]() $[u]_R=T_n\setminus S_n$
if
$[u]_R=T_n\setminus S_n$
if
![]() $u\notin S_n$
. To be precise, let us prove that
$u\notin S_n$
. To be precise, let us prove that
The implication to the right in Equation (3-3) follows from the fact that
![]() $[u]_R\subseteq S_n$
for each
$[u]_R\subseteq S_n$
for each
![]() $u\in S_n$
. To see this, recall that
$u\in S_n$
. To see this, recall that
![]() $(u,v)\in R$
if and only if there exists a finite sequence
$(u,v)\in R$
if and only if there exists a finite sequence
![]() $w_0,\ldots ,w_k$
of elements in
$w_0,\ldots ,w_k$
of elements in
![]() $T_n$
such that
$T_n$
such that
![]() $u=w_0$
,
$u=w_0$
,
![]() $v=w_k$
, and for each
$v=w_k$
, and for each
![]() $i\in \{0,1,\ldots ,k-1\}$
, either
$i\in \{0,1,\ldots ,k-1\}$
, either
![]() $w_i$
or
$w_i$
or
![]() $w_{i+1}$
is an elementary
$w_{i+1}$
is an elementary
![]() $A_n$
-deformation of the other. Actually, since
$A_n$
-deformation of the other. Actually, since
![]() $A_n$
is a group, both conditions are equivalent. For instance, if
$A_n$
is a group, both conditions are equivalent. For instance, if
![]() $w_{i+1}=z_1\tau z_2$
for some
$w_{i+1}=z_1\tau z_2$
for some
![]() $z_1,z_2\in T_n$
such that
$z_1,z_2\in T_n$
such that
![]() $w_i=z_1z_2$
and some
$w_i=z_1z_2$
and some
![]() $\tau \in A_n$
, then
$\tau \in A_n$
, then
![]() $w_i=(z_1\tau )\tau ^{-1} z_2$
. Therefore, it is enough to see that every elementary
$w_i=(z_1\tau )\tau ^{-1} z_2$
. Therefore, it is enough to see that every elementary
![]() $A_n$
-deformation of an element in
$A_n$
-deformation of an element in
![]() $S_n$
is still in
$S_n$
is still in
![]() $S_n$
, and this is clearly true because every factorization of an element in
$S_n$
, and this is clearly true because every factorization of an element in
![]() $S_n$
is necessarily as a composite of elements in
$S_n$
is necessarily as a composite of elements in
![]() $S_n$
. To prove the converse, we proceed again by induction on the rank r of u. If
$S_n$
. To prove the converse, we proceed again by induction on the rank r of u. If
![]() $r=1$
, then u is the constant map
$r=1$
, then u is the constant map
![]() $c_i$
for some
$c_i$
for some
![]() $i\in \mathbf {n}$
, and when
$i\in \mathbf {n}$
, and when
![]() $i\neq 1$
, the map
$i\neq 1$
, the map
![]() $c_1$
is the composite of
$c_1$
is the composite of
![]() $c_i$
and the permutation
$c_i$
and the permutation
![]() $(1ji)\in A_n$
for some
$(1ji)\in A_n$
for some
![]() $j\neq 1,i$
(here we use that
$j\neq 1,i$
(here we use that
![]() $n\geq 3$
). Hence,
$n\geq 3$
). Hence,
![]() $(u,c_1)\in R$
. Let us now assume that for some
$(u,c_1)\in R$
. Let us now assume that for some
![]() $r\in \{1,\ldots ,n-2\}$
, every map of rank r is R-related to
$r\in \{1,\ldots ,n-2\}$
, every map of rank r is R-related to
![]() $c_1$
, and let u be of rank
$c_1$
, and let u be of rank
![]() $r+1$
. Let i be not in the image of u, j any element in the image of u, and l such that
$r+1$
. Let i be not in the image of u, j any element in the image of u, and l such that
![]() $u(l)\neq j$
(we are using again that
$u(l)\neq j$
(we are using again that
![]() $n\geq 3$
), and let
$n\geq 3$
), and let
![]() $u':\mathbf {n}\to \mathbf {n}$
be the same map as in the proof of the previous proposition. In particular, we have
$u':\mathbf {n}\to \mathbf {n}$
be the same map as in the proof of the previous proposition. In particular, we have
![]() $u'u=u$
. Then the composite
$u'u=u$
. Then the composite
![]() $\tilde {u}=u'\sigma u$
with
$\tilde {u}=u'\sigma u$
with
![]() $\sigma $
the permutation
$\sigma $
the permutation
![]() $(iu(l)j)\in A_n$
is an elementary
$(iu(l)j)\in A_n$
is an elementary
![]() $A_n$
-deformation of u and consequently,
$A_n$
-deformation of u and consequently,
![]() $(u,\tilde {u})\in R$
. However,
$(u,\tilde {u})\in R$
. However,
![]() $\tilde {u}$
is of rank r because all elements in
$\tilde {u}$
is of rank r because all elements in
![]() $u^{-1}(u(l))$
are now mapped to j, while
$u^{-1}(u(l))$
are now mapped to j, while
![]() $\tilde {u}(k)=u(k)$
for each
$\tilde {u}(k)=u(k)$
for each
![]() $k\notin u^{-1}(u(l))$
. Indeed,
$k\notin u^{-1}(u(l))$
. Indeed,
![]() $\sigma u$
maps all of
$\sigma u$
maps all of
![]() $u^{-1}(j)$
to i, but this is next mapped again to j by
$u^{-1}(j)$
to i, but this is next mapped again to j by
![]() $u'$
. By the induction hypothesis,
$u'$
. By the induction hypothesis,
![]() $(\tilde {u},c_1)\in R$
and hence,
$(\tilde {u},c_1)\in R$
and hence,
![]() $(u,c_1)\in R$
. This proves Equation (3-3).
$(u,c_1)\in R$
. This proves Equation (3-3).
Let us now prove Equation (3-4). The implication to the right follows now from the fact that for every odd permutation (for instance,
![]() $(12)$
),
$(12)$
),
![]() $[\sigma ]_R\subseteq S_n\setminus A_n$
. Indeed, every factorization of an odd permutation is necessarily as a composite of an odd and an even permutation, and hence, every elementary
$[\sigma ]_R\subseteq S_n\setminus A_n$
. Indeed, every factorization of an odd permutation is necessarily as a composite of an odd and an even permutation, and hence, every elementary
![]() $A_n$
-deformation of it is also an odd permutation. The converse follows from the obvious fact that every odd permutation u can be connected to
$A_n$
-deformation of it is also an odd permutation. The converse follows from the obvious fact that every odd permutation u can be connected to
![]() $(12)$
by a finite number of elementary
$(12)$
by a finite number of elementary
![]() $A_n$
-deformations. It is enough to write u as the composite of an odd number of transpositions including
$A_n$
-deformations. It is enough to write u as the composite of an odd number of transpositions including
![]() $(12)$
(two consecutive times if necessary), and then proceed to eliminate consecutive pairs of transpositions by performing elementary
$(12)$
(two consecutive times if necessary), and then proceed to eliminate consecutive pairs of transpositions by performing elementary
![]() $A_n$
-deformations until we are left only with the transposition
$A_n$
-deformations until we are left only with the transposition
![]() $(12)$
. This proves Equation (3-4).
$(12)$
. This proves Equation (3-4).
By an easy case-by-case check, it follows that the map
![]() $T_n\to \{-1,0,1\}$
sending each
$T_n\to \{-1,0,1\}$
sending each
![]() $u\notin S_n$
to
$u\notin S_n$
to
![]() $0$
, each
$0$
, each
![]() $u\in A_n$
to
$u\in A_n$
to
![]() $1$
, and each
$1$
, and each
![]() $u\in S_n\setminus A_n$
to
$u\in S_n\setminus A_n$
to
![]() $-1$
preserves products and hence, is a monoid epimorphism that factors through the quotient
$-1$
preserves products and hence, is a monoid epimorphism that factors through the quotient
![]() $T_n/A_n$
, and whose induced map
$T_n/A_n$
, and whose induced map
![]() $T_n/A_n\to \{-1,0,1\}$
is a monoid isomorphism.
$T_n/A_n\to \{-1,0,1\}$
is a monoid isomorphism.
Corollary 3.20.
![]() $T_n$
is congruentially simple for each
$T_n$
is congruentially simple for each
![]() $n\geq 5$
.
$n\geq 5$
.
Proof. Neither of the monoids in Proposition 3.19 has unital congruences other than the equality.
4 Final comments
There remain many open questions in this work which are left for future work. Let us mention a few of them.
(1) There is first the question of the modularity of the lattice of normal submonoids of a monoid. Although it is unlikely that every monoid is modular, we have no example of a monoid whose lattice is not modular. Assuming that example exists, it will be interesting to identify where the modularity of a monoid is hidden, namely, a necessary and sufficient condition for a monoid to be modular.
(2) There is also the question of the normality of a monoid, and the associated question of the normal simplicity when the monoid is normal. Although it seems possible that the group of units of a monoid is always a normal submonoid of it, we have not been able to prove it. In any case, it is clear that not every normal monoid is normally simple, as the example of the additive monoid of natural numbers shows. Therefore, it will also be interesting to identify necessary and/or sufficient conditions for a normal monoid to be normally simple.
(3) Of course, there is the problem of describing the normal submonoids of some important examples of monoids, in particular, the special transformation, combinatorial, endomorphisms, or diagram monoids.
(4) We have seen that congruences on a monoid can be naturally classified into normal congruences and exceptional ones. Congruences of the last type are those for which there exists a strictly smaller congruence having the same normal submonoid as the equivalence class of the identity element. The question arises whether exceptional congruences only exist for the trivial submonoid, as is the case of both
![]() $\mathbb {N}_+$
and the finite full transformations monoids, or they also exist for other normal submonoids. This is the question of determining whether every monoid is congruentially simple or not. If not, the problem arises of determining which normal submonoids of a noncongruentially simple monoid might be called ‘congruentially complete’, that is, such that there is only one congruence with this normal submonoid as the equivalence class of the identity element (equivalently, such that the normal quotient has no unital congruence other than the equality).
$\mathbb {N}_+$
and the finite full transformations monoids, or they also exist for other normal submonoids. This is the question of determining whether every monoid is congruentially simple or not. If not, the problem arises of determining which normal submonoids of a noncongruentially simple monoid might be called ‘congruentially complete’, that is, such that there is only one congruence with this normal submonoid as the equivalence class of the identity element (equivalently, such that the normal quotient has no unital congruence other than the equality).
(5) We have shown that, in general, the lattice of normal submonoids of a monoid can be identified with just a join subsemilattice of the whole lattice of congruences on it. Are the groups the only monoids for which
![]() $\mathsf {NorSub}(M)$
and
$\mathsf {NorSub}(M)$
and
![]() $\mathsf {Cong}(M)$
are isomorphic?
$\mathsf {Cong}(M)$
are isomorphic?
(6) We have seen a way of reducing the computation of the congruences on a monoid to being able to compute the unital ones. What input or inputs in the monoid determine a unital congruence? In other words, what additional input or inputs, together with the equivalence class of the identity element, determine completely a congruence on a monoid? Here, the lattice of ideals and the set of nonidentity idempotents of the monoid perhaps play a crucial role. In fact, in the case of groups, both things collapse.
Finally, it remains the problem of extending, if possible, the whole theory to arbitrary semigroups or, at least, to some important types of semigroups (nilpotent, perfect, and so forth). In fact, there already exist various notions of a normal subsemigroup, each of them related to a particular notion of conjugacy for semigroups. The question naturally arises whether some of these notions provides the appropriate generalization to semigroups of the notion of normal submonoid as defined in this work.