Article contents
A note on interpretations of many-sorted theories
Published online by Cambridge University Press: 12 March 2014
Extract
Whenever many-sorted theories are discussed in logic texts (e.g., [3, pp. 483–485]), it is fashionable to observe that every many-sorted theory 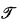 can be effectively replaced by an equally powerful one-sorted theory
can be effectively replaced by an equally powerful one-sorted theory 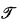 *. The theory
*. The theory 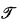 * contains for each sort σ of
* contains for each sort σ of 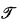 a unary predicate symbol Sσ used to indicate that an individual is of sort σ; the nonlogical axioms of
a unary predicate symbol Sσ used to indicate that an individual is of sort σ; the nonlogical axioms of 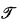 * are the “translations” of those of
* are the “translations” of those of 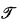 together with axioms asserting that there is at least one individual of each sort and that all function symbols behave properly with respect to sorts. This observation suggests that perhaps many-sorted theories are no more useful than one-sorted theories. That this is not always the case has been pointed out previously [1, p. 13]. The content of this note is that
together with axioms asserting that there is at least one individual of each sort and that all function symbols behave properly with respect to sorts. This observation suggests that perhaps many-sorted theories are no more useful than one-sorted theories. That this is not always the case has been pointed out previously [1, p. 13]. The content of this note is that 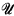 can be interpretable in
can be interpretable in 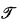 without
without 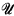 * being interpretable in
* being interpretable in 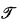 *.
*.
If a function symbol f in a many-sorted theory takes as its arguments n terms a1,…, an of sorts σ1, …, σn, respectively and produces a term fa1 … an of sort σ, then f is said to be of type (σ1, …, σn;σ). Likewise, a predicate symbol is of type (σ1, …, σn) if it takes as its arguments n terms of sorts σ1, …, σn. We assume that for each sort σ there is a predicate symbol = σ of type (σ, σ).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 3
- Cited by


