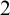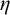1 Introduction
The study of this article is aimed at describing algebraic properties of structures having computable presentations. Feiner [Reference Feiner3] constructed a
![]() $\emptyset '$
-computable Boolean algebra with no computable presentation. An analysis of his proof shows that this Boolean algebra does not even have a low
$\emptyset '$
-computable Boolean algebra with no computable presentation. An analysis of his proof shows that this Boolean algebra does not even have a low
![]() $_n$
presentation for any natural n. There was the conjecture that every low
$_n$
presentation for any natural n. There was the conjecture that every low
![]() $_n$
Boolean algebra has a computable representation. Jockusch and Downey [Reference Jockusch and Downey11] confirmed this hypothesis for
$_n$
Boolean algebra has a computable representation. Jockusch and Downey [Reference Jockusch and Downey11] confirmed this hypothesis for
![]() $n=1$
. Since every Boolean algebra is generated by a linear order, similar questions were asked for the class of linear orders. Feiner [Reference Feiner2] constructed a
$n=1$
. Since every Boolean algebra is generated by a linear order, similar questions were asked for the class of linear orders. Feiner [Reference Feiner2] constructed a
![]() $\emptyset '$
-computable linear order which has no computable presentation.
$\emptyset '$
-computable linear order which has no computable presentation.
J. Knight (unpublished) stated the question of the existence of a computable copy for every low linear order. However, Soare and Jockusch [Reference Soare and Jockusch17] disproved this hypothesis by constructing a low linear order without a computable copy (in fact, they constructed such an order in each nonzero computably enumerable degree). On the other hand, Moses and Downey [Reference Moses and Downey15] proved that each low discrete linear order has a computable copy (a linear order is discrete if it has no limit points). From these results, the following question naturally arises (in fact, a whole research program), which was asked in 1998 in Downey’s survey [Reference Downey, Ershov, Goncharov, Nerode and Remmel1]: describe a property P of classical order types that guarantee that if
![]() $\mathcal {L}$
is a low linear order and P holds for the order type of
$\mathcal {L}$
is a low linear order and P holds for the order type of
![]() $\mathcal {L}$
then
$\mathcal {L}$
then
![]() $\mathcal {L}$
is isomorphic to a computable linear order.
$\mathcal {L}$
is isomorphic to a computable linear order.
In terms of order types, various partial solutions to Downey’s question were obtained. Initially, Frolov [Reference Frolov5] showed that every low strongly
![]() $\eta $
-like linear order has a computable copy. Later, he also generalized this result [Reference Frolov6]: every low k-quasidiscrete linear order has a computable copy (a linear order is called k-quasidiscrete if it has only infinite blocks and maximal blocks of sizes not greater than k). The first result can be improved in the other direction: if a low linear order with
$\eta $
-like linear order has a computable copy. Later, he also generalized this result [Reference Frolov6]: every low k-quasidiscrete linear order has a computable copy (a linear order is called k-quasidiscrete if it has only infinite blocks and maximal blocks of sizes not greater than k). The first result can be improved in the other direction: if a low linear order with
![]() $\eta $
condensation has no strongly
$\eta $
condensation has no strongly
![]() $\eta $
-like subinterval then it has a computable copy [Reference Frolov7]. Also, we would like to note the result of Zubkov [Reference Zubkov23]. He introduced the left and right local maximal blocks and proved that if sizes of the left and right local maximal blocks of a low
$\eta $
-like subinterval then it has a computable copy [Reference Frolov7]. Also, we would like to note the result of Zubkov [Reference Zubkov23]. He introduced the left and right local maximal blocks and proved that if sizes of the left and right local maximal blocks of a low
![]() $\eta $
-like linear order are bounded by a fixed number then the order type of this linear order can be described by a
$\eta $
-like linear order are bounded by a fixed number then the order type of this linear order can be described by a
![]() $\emptyset '$
-limitwise monotonic function on rationals, and, consequently, this linear order has a computable copy (see, [Reference Frolov and Zubkov10, Reference Zubkov and Frolov24]). The following two results about low
$\emptyset '$
-limitwise monotonic function on rationals, and, consequently, this linear order has a computable copy (see, [Reference Frolov and Zubkov10, Reference Zubkov and Frolov24]). The following two results about low
![]() $_n$
linear orders are worth mentioning. The first result is the result of Thurber, Alaev, and Frolov [Reference Thurber, Alaev and Frolov18]. They proved that every low
$_n$
linear orders are worth mentioning. The first result is the result of Thurber, Alaev, and Frolov [Reference Thurber, Alaev and Frolov18]. They proved that every low
![]() $_2 1$
-quasidiscrete linear order is computably presentable. The second one was obtained by Montalbán and Kach [Reference Montalbán and Kach14]. They proved that if a linear order is low
$_2 1$
-quasidiscrete linear order is computably presentable. The second one was obtained by Montalbán and Kach [Reference Montalbán and Kach14]. They proved that if a linear order is low
![]() $_n$
and has only finitely many descending cuts then it has a computable copy.
$_n$
and has only finitely many descending cuts then it has a computable copy.
The complete solution to Downey’s problem seems to the authors extremely difficult and hardly possible. Therefore, as mentioned above, this is more likely a research program but not just a question. The fact is that besides positive partial results there are several negative ones. For example, Frolov [Reference Frolov8] constructed a low
![]() $_2$
scattered linear order that does not have a computable presentation. The question of whether every low scattered linear order has a computable presentation remains open. Also, Frolov [Reference Frolov9] constructed a low
$_2$
scattered linear order that does not have a computable presentation. The question of whether every low scattered linear order has a computable presentation remains open. Also, Frolov [Reference Frolov9] constructed a low
![]() $\eta $
-like linear order that does not have a computable copy (the cited paper is a survey where the reader could find more results).
$\eta $
-like linear order that does not have a computable copy (the cited paper is a survey where the reader could find more results).
Let us discuss the last result in more detail. As mentioned above, Soare and Jockusch [Reference Soare and Jockusch17] constructed a low linear order which does not have a computable copy. This linear order has the Hausdorff rank equal to
![]() $2$
. Frolov [Reference Frolov9] constructed a low
$2$
. Frolov [Reference Frolov9] constructed a low
![]() $\eta $
-like linear order with no computable copy. Note that an
$\eta $
-like linear order with no computable copy. Note that an
![]() $\eta $
-like linear order has Hausdorff rank equal to
$\eta $
-like linear order has Hausdorff rank equal to
![]() $1$
, so it has the least possible Hausdorff rank. However, the non-singleton blocks (i.e., blocks with at least two elements) in the order constructed by Frolov are arranged in a rather complex way. Note that non-singleton blocks of an arbitrary
$1$
, so it has the least possible Hausdorff rank. However, the non-singleton blocks (i.e., blocks with at least two elements) in the order constructed by Frolov are arranged in a rather complex way. Note that non-singleton blocks of an arbitrary
![]() $\eta $
-like linear order can have any ordering. For example,
$\eta $
-like linear order can have any ordering. For example,
![]() $(\eta + 2 + \eta ) \cdot \mathcal {L}$
is
$(\eta + 2 + \eta ) \cdot \mathcal {L}$
is
![]() $\eta $
-like, and the order types of
$\eta $
-like, and the order types of
![]() $\mathcal {L}$
and the set of its non-singleton blocks are the same, where
$\mathcal {L}$
and the set of its non-singleton blocks are the same, where
![]() $\mathcal {L}$
can be any linear order. The low linear order with no computable copy constructed by Frolov is an
$\mathcal {L}$
can be any linear order. The low linear order with no computable copy constructed by Frolov is an
![]() $\omega $
-sum of strongly
$\omega $
-sum of strongly
![]() $\eta $
-representations of sets and, consequently, non-singleton blocks ordered as
$\eta $
-representations of sets and, consequently, non-singleton blocks ordered as
![]() $\omega ^2\kern-1.2pt$
. Could we simplify it? Namely, the following question arises: is there a low linear order with no computable copy which is (a strongly) an
$\omega ^2\kern-1.2pt$
. Could we simplify it? Namely, the following question arises: is there a low linear order with no computable copy which is (a strongly) an
![]() $\eta $
-representation of a set? In this paper, we answer positively to this question (Theorem 2.2).
$\eta $
-representation of a set? In this paper, we answer positively to this question (Theorem 2.2).
Note that
![]() $\eta $
-representations are the simplest orders which are not satisfying all known at this moment properties P from Downey’s question above. Let us recall the definition of an
$\eta $
-representations are the simplest orders which are not satisfying all known at this moment properties P from Downey’s question above. Let us recall the definition of an
![]() $\eta $
-representation. Let
$\eta $
-representation. Let
![]() $\{a_0,\,a_1,\,a_2, \dots \}$
be an enumeration of a set
$\{a_0,\,a_1,\,a_2, \dots \}$
be an enumeration of a set
![]() $A\subseteq \omega $
, perhaps with repetitions. Then a linear order
$A\subseteq \omega $
, perhaps with repetitions. Then a linear order
![]() $\mathcal {L}$
of the order type
$\mathcal {L}$
of the order type
![]() $\eta +a_0+\eta +a_1+\eta +a_2+\eta +\cdots $
is called an
$\eta +a_0+\eta +a_1+\eta +a_2+\eta +\cdots $
is called an
![]() $\eta $
-representation of the set A. If the enumeration is with no repetitions then the
$\eta $
-representation of the set A. If the enumeration is with no repetitions then the
![]() $\eta $
-representation is called injective; if the enumeration is in the non-decreasing order then it is called a non-decreasing
$\eta $
-representation is called injective; if the enumeration is in the non-decreasing order then it is called a non-decreasing
![]() $\eta $
-representation; and if the enumeration is increasing then it is called a strongly
$\eta $
-representation; and if the enumeration is increasing then it is called a strongly
![]() $\eta $
-representation.
$\eta $
-representation.
Despite the simplicity of these order types and various obtained results, the study of theoretical computability properties of
![]() $\eta $
-representations and especially strong
$\eta $
-representations and especially strong
![]() $\eta $
-representations encounter many serious difficulties. By direct arguments, Feiner [Reference Feiner3] showed that
$\eta $
-representations encounter many serious difficulties. By direct arguments, Feiner [Reference Feiner3] showed that
![]() $\eta $
-representable sets (that is, sets having computable
$\eta $
-representable sets (that is, sets having computable
![]() $\eta $
-representations) belong to the
$\eta $
-representations) belong to the
![]() $\Sigma ^0_3$
-level of the arithmetical hierarchy. On the other hand, Rosenstein [Reference Rosenstein16] and Fellner [Reference Fellner4] coded any
$\Sigma ^0_3$
-level of the arithmetical hierarchy. On the other hand, Rosenstein [Reference Rosenstein16] and Fellner [Reference Fellner4] coded any
![]() $\Sigma ^0_2$
-set and
$\Sigma ^0_2$
-set and
![]() $\Pi ^0_2$
-set, correspondingly, into a computable strong
$\Pi ^0_2$
-set, correspondingly, into a computable strong
![]() $\eta $
-representation. This result was improved by Zubkov [Reference Zubkov21]: if A is
$\eta $
-representation. This result was improved by Zubkov [Reference Zubkov21]: if A is
![]() $\Sigma ^0_2$
and B is
$\Sigma ^0_2$
and B is
![]() $\Pi ^0_2$
then
$\Pi ^0_2$
then
![]() $A\bigcup B$
is strongly
$A\bigcup B$
is strongly
![]() $\eta $
-representable. Thus, there is a “gap” between the upper and lower bounds of the levels of the arithmetic hierarchy of sets that have computable
$\eta $
-representable. Thus, there is a “gap” between the upper and lower bounds of the levels of the arithmetic hierarchy of sets that have computable
![]() $\eta $
-representations. Lerman built a
$\eta $
-representations. Lerman built a
![]() $\Sigma ^0_3$
-set without a computable
$\Sigma ^0_3$
-set without a computable
![]() $\eta $
-representation. Rosenstein showed that any strongly
$\eta $
-representation. Rosenstein showed that any strongly
![]() $\eta $
-representable set is
$\eta $
-representable set is
![]() $\Delta ^0_3$
. In fact, he proved that every non-decreasing
$\Delta ^0_3$
. In fact, he proved that every non-decreasing
![]() $\eta $
-representable set belongs to
$\eta $
-representable set belongs to
![]() $\Delta ^0_3$
. In the same paper, Rosenstein stated the question of describing strongly
$\Delta ^0_3$
. In the same paper, Rosenstein stated the question of describing strongly
![]() $\eta $
-representable sets. However, this is a difficult problem, and at least from the above results it follows that there is no such description in the arithmetical hierarchy. Downey [Reference Downey, Ershov, Goncharov, Nerode and Remmel1] asked a weaker question of describing at least strongly
$\eta $
-representable sets. However, this is a difficult problem, and at least from the above results it follows that there is no such description in the arithmetical hierarchy. Downey [Reference Downey, Ershov, Goncharov, Nerode and Remmel1] asked a weaker question of describing at least strongly
![]() $\eta $
-representable degrees. A series of results was obtained in this direction, also.
$\eta $
-representable degrees. A series of results was obtained in this direction, also.
Lerman [Reference Lerman, Lerman, Schmerl and Soare12] proved that a degree is
![]() $\eta $
-representable if and only if it is computably enumerable relatively to
$\eta $
-representable if and only if it is computably enumerable relatively to
![]() $\emptyset "$
. Frolov and Zubkov [Reference Zubkov and Frolov24] and Turetsky and Kach [Reference Turetsky and Kach20], independently, proved that a degree is increasing
$\emptyset "$
. Frolov and Zubkov [Reference Zubkov and Frolov24] and Turetsky and Kach [Reference Turetsky and Kach20], independently, proved that a degree is increasing
![]() $\eta $
-representable if and only if it is
$\eta $
-representable if and only if it is
![]() $\emptyset "$
-computable. We will note here only one more result obtained by Zubkov [Reference Zubkov22]. A degree is strongly
$\emptyset "$
-computable. We will note here only one more result obtained by Zubkov [Reference Zubkov22]. A degree is strongly
![]() $\eta $
-representable if and only if it has the range of a
$\eta $
-representable if and only if it has the range of a
![]() $\emptyset '$
-limitwise monotonic function
$\emptyset '$
-limitwise monotonic function
![]() which satisfies the following conditions:
which satisfies the following conditions:
![]() $f(x)\geq 1$
for all x, the set of x such that
$f(x)\geq 1$
for all x, the set of x such that
![]() $f(x)> 1$
is ordered as
$f(x)> 1$
is ordered as
![]() $\omega $
, and if
$\omega $
, and if
![]() $f(x), f(y)> 1$
and
$f(x), f(y)> 1$
and
![]() then
then
![]() . More detailed surveys could be found in [Reference Frolov and Zubkov10, Reference Turetsky, Downey, Kach, Arai, Feng, Kim, Wu and Yang19].
. More detailed surveys could be found in [Reference Frolov and Zubkov10, Reference Turetsky, Downey, Kach, Arai, Feng, Kim, Wu and Yang19].
Note here that the results above can be translated without changes to low
![]() $\eta $
-representations and low strong
$\eta $
-representations and low strong
![]() $\eta $
-representations, correspondingly. Consequently, the class of degrees of sets having computable
$\eta $
-representations, correspondingly. Consequently, the class of degrees of sets having computable
![]() $\eta $
-representations (strong
$\eta $
-representations (strong
![]() $\eta $
-representations) coincides with the class of degrees of sets with low
$\eta $
-representations) coincides with the class of degrees of sets with low
![]() $\eta $
-representations (strong
$\eta $
-representations (strong
![]() $\eta $
-representations). Thus, the coding techniques for
$\eta $
-representations). Thus, the coding techniques for
![]() $\eta $
-representations above are not enough to construct a low strong
$\eta $
-representations above are not enough to construct a low strong
![]() $\eta $
-representation without a computable copy. We propose a new technique that allows us to prove that the classes of sets having computable (strong)
$\eta $
-representation without a computable copy. We propose a new technique that allows us to prove that the classes of sets having computable (strong)
![]() $\eta $
-representations and low (strong)
$\eta $
-representations and low (strong)
![]() $\eta $
-representations are different. Then the following question naturally arises.
$\eta $
-representations are different. Then the following question naturally arises.
Question 1.1. Describe sets that have a low (strongly)
![]() $\eta $
-representation but have no computable one.
$\eta $
-representation but have no computable one.
2 The main result and an informal description of the construction
Recall that a computable linear order is called (relatively)
![]() $\Delta ^0_n$
-categorical if, for any two computable (X-computable, correspondingly) its representations, there exists a
$\Delta ^0_n$
-categorical if, for any two computable (X-computable, correspondingly) its representations, there exists a
![]() $\Delta ^0_n$
-isomorphism (
$\Delta ^0_n$
-isomorphism (
![]() $\Delta ^X_n$
-isomorphism, correspondingly) between them (n is a natural number). Before going to the main result we prove the following non-difficult fact.
$\Delta ^X_n$
-isomorphism, correspondingly) between them (n is a natural number). Before going to the main result we prove the following non-difficult fact.
Lemma 2.1. Every
![]() $\eta $
-representation is relatively
$\eta $
-representation is relatively
![]() $\Delta ^0_3$
-categorical.
$\Delta ^0_3$
-categorical.
Proof Let
![]() $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
![]() $\mathcal {L}_2$
be two isomorphic
$\mathcal {L}_2$
be two isomorphic
![]() $\eta $
-representations. Then we can find finite blocks and dense intervals inside both linear orders using the oracle
$\eta $
-representations. Then we can find finite blocks and dense intervals inside both linear orders using the oracle
![]() $(\mathcal {L}_1\oplus \mathcal {L}_2)"$
. Moreover, we can find the i-th non-singleton block by the sequential finding of the first block, of the second block, etc. The first block is the block that has no successors to the left, the second block is the block that has no successors between it and the first block, and so on. Thus, we can compute an isomorphism using the specified oracle. Namely, we map the i-th non-singleton block of the first linear order to the i-th non-singleton block of the second linear order and dense intervals between non-singleton blocks of the first order to dense intervals between corresponding non-singleton blocks of the second order.
$(\mathcal {L}_1\oplus \mathcal {L}_2)"$
. Moreover, we can find the i-th non-singleton block by the sequential finding of the first block, of the second block, etc. The first block is the block that has no successors to the left, the second block is the block that has no successors between it and the first block, and so on. Thus, we can compute an isomorphism using the specified oracle. Namely, we map the i-th non-singleton block of the first linear order to the i-th non-singleton block of the second linear order and dense intervals between non-singleton blocks of the first order to dense intervals between corresponding non-singleton blocks of the second order.
Theorem 2.2. There exists a low strongly
![]() $\eta $
-representation with no computable copy.
$\eta $
-representation with no computable copy.
Proof. As known (see [Reference Montalban, Ambos-Spies, Löwe and Merkle13] or [Reference Frolov6]), a linear order
![]() $\mathcal {L}$
has a low copy if and only if it has a
$\mathcal {L}$
has a low copy if and only if it has a
![]() $\emptyset '$
-computable copy with the
$\emptyset '$
-computable copy with the
![]() $\emptyset '$
-computable successor relation. Therefore, it is enough to construct a
$\emptyset '$
-computable successor relation. Therefore, it is enough to construct a
![]() $\emptyset '$
-computable linear order with the
$\emptyset '$
-computable linear order with the
![]() $\emptyset '$
-computable successor relation which is a strong
$\emptyset '$
-computable successor relation which is a strong
![]() $\eta $
-representation. So, the construction uses a
$\eta $
-representation. So, the construction uses a
![]() $\emptyset '$
-oracle.
$\emptyset '$
-oracle.
Every computable linear order is computably isomorphic to a c.e. subset of rationals (see, for example, [Reference Downey, Ershov, Goncharov, Nerode and Remmel1]). Abusing the notation, let
![]() $\{W_e\}_{e\in \omega }$
be a computable enumeration of all c.e. subsets of
$\{W_e\}_{e\in \omega }$
be a computable enumeration of all c.e. subsets of
![]() . We will denote the induced linear order on a c.e. subset in the same way as
. We will denote the induced linear order on a c.e. subset in the same way as
![]() $W_e$
.
$W_e$
.
We construct
![]() $\mathcal {L}\leq _T \emptyset '$
with successor relation
$\mathcal {L}\leq _T \emptyset '$
with successor relation
![]() $S_{\mathcal {L}}\leq _T \emptyset '$
meeting
$S_{\mathcal {L}}\leq _T \emptyset '$
meeting
We note that the requirements do indeed prove the theorem: by the lemma above, if
![]() $\mathcal {L}$
has a computable copy
$\mathcal {L}$
has a computable copy
![]() $\mathcal {L}'$
then there is a
$\mathcal {L}'$
then there is a
![]() $\emptyset "$
-computable isomorphism between
$\emptyset "$
-computable isomorphism between
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {L}'$
.
$\mathcal {L}'$
.
Since we are using a
![]() $\emptyset '$
-oracle, we will be approximating
$\emptyset '$
-oracle, we will be approximating
![]() $\varphi _e^{\emptyset "}$
using the Limit Lemma in relativized form, and hence considering
$\varphi _e^{\emptyset "}$
using the Limit Lemma in relativized form, and hence considering
![]() $\lim \limits _s\varphi _e^{\emptyset '}(x,s)$
as a Limit Lemma approximation to
$\lim \limits _s\varphi _e^{\emptyset '}(x,s)$
as a Limit Lemma approximation to
![]() $\varphi _e^{\emptyset "}$
, and this is only
$\varphi _e^{\emptyset "}$
, and this is only
![]() $\Sigma ^0_2$
. The strategy is either to show that this limit does not exist, or to show that for some argument, if it exists then it is wrong. So, either force it to change infinitely often for some x, or force it to give a wrong value. We are using both
$\Sigma ^0_2$
. The strategy is either to show that this limit does not exist, or to show that for some argument, if it exists then it is wrong. So, either force it to change infinitely often for some x, or force it to give a wrong value. We are using both
![]() $\varphi _e^{\emptyset '}(x)[s]$
and
$\varphi _e^{\emptyset '}(x)[s]$
and
![]() $\varphi _e^{\emptyset '}(x,s)$
, for this approximation interchangeably.
$\varphi _e^{\emptyset '}(x,s)$
, for this approximation interchangeably.
The informal description is organized as follows: the first part is a construction of the linear order, the second part is satisfying of one requirement, and the last part is an interaction of different requirement strategies.
The domain of the linear order will be
![]() $\omega $
. At each stage s we will have a finite ordering
$\omega $
. At each stage s we will have a finite ordering
![]() $\mathcal {L}_s$
. At stage
$\mathcal {L}_s$
. At stage
![]() $s + 1$
we will add points to
$s + 1$
we will add points to
![]() $\mathcal {L}_s$
to make
$\mathcal {L}_s$
to make
![]() $\mathcal {L}_{s+1}$
. To keep
$\mathcal {L}_{s+1}$
. To keep
![]() $S_{\mathcal {L}} \le _T \emptyset '$
, for each successive pair of points
$S_{\mathcal {L}} \le _T \emptyset '$
, for each successive pair of points
![]() $x <_{\mathcal {L}_{s+1}} y$
we will irrevocably declare whether this is an adjacency.
$x <_{\mathcal {L}_{s+1}} y$
we will irrevocably declare whether this is an adjacency.
The general shape of the construction is the following. At each stage, we will be building a series of blocks
![]() $B_0 <_{\mathcal {L}_s} B_1 <_{\mathcal {L}_s} \cdots $
, where initially
$B_0 <_{\mathcal {L}_s} B_1 <_{\mathcal {L}_s} \cdots $
, where initially
![]() $|B_i[s]| = 2i+2$
. This fact means that for
$|B_i[s]| = 2i+2$
. This fact means that for
![]() $B_i[s]$
we have declared
$B_i[s]$
we have declared
![]() $b_1[s],\ldots ,\, b_{2i+2}[s]$
to be
$b_1[s],\ldots ,\, b_{2i+2}[s]$
to be
![]() $2i+2$
adjacencies, so this must be a part of a block of size at least
$2i+2$
adjacencies, so this must be a part of a block of size at least
![]() $2i+2$
. To keep track of what is happening, we will declare points in blocks as x-points, and points from dense subintervals as y-points. In the construction, x-points are forever x-points, but y-points can become x-points if we suddenly decide that they are part of a block, but this can only happen with the addition of further points as we describe below.
$2i+2$
. To keep track of what is happening, we will declare points in blocks as x-points, and points from dense subintervals as y-points. In the construction, x-points are forever x-points, but y-points can become x-points if we suddenly decide that they are part of a block, but this can only happen with the addition of further points as we describe below.
Between blocks
![]() $B_i$
and
$B_i$
and
![]() $B_{i+1}$
currently we will be densifying and will have added y-points so have
$B_{i+1}$
currently we will be densifying and will have added y-points so have
![]() $xxxx \ldots xy \ldots yx \ldots x$
. The y points have been declared to be non-adjacencies, as have
$xxxx \ldots xy \ldots yx \ldots x$
. The y points have been declared to be non-adjacencies, as have
![]() $xy$
and
$xy$
and
![]() $yx$
. In the absence of any actions of the
$yx$
. In the absence of any actions of the
![]() $P_e$
’s, at every stage s we would simply add a new y-point between y-points and between x and y and between y and x. So for example,
$P_e$
’s, at every stage s we would simply add a new y-point between y-points and between x and y and between y and x. So for example,
![]() $xyyyyx$
would become
$xyyyyx$
would become
![]() $xyyyyyyyyyx$
, and declare that the new
$xyyyyyyyyyx$
, and declare that the new
![]() $yy$
’s and new
$yy$
’s and new
![]() $xy$
and
$xy$
and
![]() $yx$
are non-adjacencies.
$yx$
are non-adjacencies.
Now, because of the action of a
![]() $P_e$
, we might choose instead to make some of the y-points new x-points. This can be done by adding, for instance, a point a between two y-points and declare that
$P_e$
, we might choose instead to make some of the y-points new x-points. This can be done by adding, for instance, a point a between two y-points and declare that
![]() $ya$
and
$ya$
and
![]() $ay$
are adjacencies making
$ay$
are adjacencies making
![]() $yay$
as
$yay$
as
![]() $xxx$
part of a block of size at least
$xxx$
part of a block of size at least
![]() $3$
. Note that we also have the option of doing a similar action on the left of right ends of a current block.
$3$
. Note that we also have the option of doing a similar action on the left of right ends of a current block.
Of course, any such action must still keep the blocks in increasing order of size. For example, between
![]() $B_i[s]$
and
$B_i[s]$
and
![]() $B_{i+1}[s]$
, if we added a new partial block B, it’s size would need to be at least
$B_{i+1}[s]$
, if we added a new partial block B, it’s size would need to be at least
![]() $|B_i[s]| + 1$
, it would become the new
$|B_i[s]| + 1$
, it would become the new
![]() $B_{i+1}[s + 1]$
, and we’d also need to increase the old
$B_{i+1}[s + 1]$
, and we’d also need to increase the old
![]() $B_{i+1}[s]$
to have size larger than
$B_{i+1}[s]$
to have size larger than
![]() $B_{i+1}[s + 1]$
, and likely it would become
$B_{i+1}[s + 1]$
, and likely it would become
![]() $B_{i+2}[s + 1]$
.
$B_{i+2}[s + 1]$
.
We now turn to the description of the strategies for diagonalizing the
![]() $W_e$
. We begin by describing the basic module, for a single
$W_e$
. We begin by describing the basic module, for a single
![]() $P_0$
.
$P_0$
.
We begin working on
![]() $B_0[s] = \{x_0<_{\mathcal {L}_s} x_1\}$
and
$B_0[s] = \{x_0<_{\mathcal {L}_s} x_1\}$
and
![]() $B_1[s] = \{x_2<_{\mathcal {L}_s} x_3 <_{\mathcal {L}_s} x_4<_{\mathcal {L}_s} x_5\}$
. Currently we are densifying between the blocks.
$B_1[s] = \{x_2<_{\mathcal {L}_s} x_3 <_{\mathcal {L}_s} x_4<_{\mathcal {L}_s} x_5\}$
. Currently we are densifying between the blocks.
Case 1. (Hereinafter we give a numeration of cases as in the formal construction below). We wait till
![]() $\varphi ^{\emptyset '}_0(x_2)[s_0] = z_0$
and part of a
$\varphi ^{\emptyset '}_0(x_2)[s_0] = z_0$
and part of a
![]() $3$
-block
$3$
-block
![]() $Z_{s_0} \subset W_{e,\,s_0}$
, and
$Z_{s_0} \subset W_{e,\,s_0}$
, and
![]() $\varphi ^{\emptyset '}_0[s_0]$
looks like a partial isomorphism, taking a block
$\varphi ^{\emptyset '}_0[s_0]$
looks like a partial isomorphism, taking a block
![]() $B_0$
and
$B_0$
and
![]() $B_1$
to blocks
$B_1$
to blocks
![]() $Z_0[s_0]$
and
$Z_0[s_0]$
and
![]() $Z = Z_1[s_0]$
of the correct sizes in
$Z = Z_1[s_0]$
of the correct sizes in
![]() $W_0[s_0]$
, and
$W_0[s_0]$
, and
![]() $\emptyset '$
has declared the members of
$\emptyset '$
has declared the members of
![]() $Z_0[s_0]$
and
$Z_0[s_0]$
and
![]() $Z = Z_1[s_0]$
to be adjacencies in
$Z = Z_1[s_0]$
to be adjacencies in
![]() $W_0$
(
$W_0$
(
![]() $\Sigma ^0_1$
-questions). Should this not happen, we will have diagonalized
$\Sigma ^0_1$
-questions). Should this not happen, we will have diagonalized
![]() $W_0$
by luck.
$W_0$
by luck.
The overall plan is to make
![]() $z_0$
have no stable pre-image in
$z_0$
have no stable pre-image in
![]() $\mathcal {L}$
, by making
$\mathcal {L}$
, by making
![]() $|Z_s|\to \infty $
, or to diagonalize at some finite stage.
$|Z_s|\to \infty $
, or to diagonalize at some finite stage.
Now, assuming we have reached stage
![]() $s_0$
. Let
$s_0$
. Let
![]() $p_0$
be the number of elements between
$p_0$
be the number of elements between
![]() $B_0[s_0]$
and
$B_0[s_0]$
and
![]() $B_1[s_0]$
. Using
$B_1[s_0]$
. Using
![]() $s_0$
, we can figure out if there are strictly more than
$s_0$
, we can figure out if there are strictly more than
![]() $2p_0 + 1$
many elements of
$2p_0 + 1$
many elements of
![]() $W_0$
between
$W_0$
between
![]() $Z_0[s_0]$
and
$Z_0[s_0]$
and
![]() $Z = Z_1[s_0]$
, as this only involves
$Z = Z_1[s_0]$
, as this only involves
![]() $\Sigma ^0_1$
-questions about
$\Sigma ^0_1$
-questions about
![]() $W_0$
.
$W_0$
.
Case 2.2. If there are not, then there are no more than
![]() $2p_0+1$
many elements between
$2p_0+1$
many elements between
![]() $Z_0[s_0]$
and
$Z_0[s_0]$
and
![]() $Z = Z_1[s_0]$
, and hence both
$Z = Z_1[s_0]$
, and hence both
![]() $Z_0[s_0]$
and
$Z_0[s_0]$
and
![]() $Z = Z_1[s_0]$
are part of the same block, which we think of as
$Z = Z_1[s_0]$
are part of the same block, which we think of as
![]() $Z_{s_0+1}$
. In this case, we will simply continue to densify between
$Z_{s_0+1}$
. In this case, we will simply continue to densify between
![]() $B_0$
and
$B_0$
and
![]() $B_1$
giving, in the limit a
$B_1$
giving, in the limit a
![]() $2$
-block followed by a
$2$
-block followed by a
![]() $4$
-block. Neither can be a pre-image of
$4$
-block. Neither can be a pre-image of
![]() $Z = \lim \limits _s Z_s$
, which must find a pre-image later in the
$Z = \lim \limits _s Z_s$
, which must find a pre-image later in the
![]() $\mathcal {L}$
-ordering.
$\mathcal {L}$
-ordering.
Case 2.3. There are strictly more than
![]() $2p_0 + 1$
many points between
$2p_0 + 1$
many points between
![]() $Z_0[s_0]$
and
$Z_0[s_0]$
and
![]() $Z = Z_1[s_0]$
. In this case, we will amalgamate the two blocks
$Z = Z_1[s_0]$
. In this case, we will amalgamate the two blocks
![]() $B_0$
and
$B_0$
and
![]() $B_1$
by turning all the y-points between them into x-points by adding
$B_1$
by turning all the y-points between them into x-points by adding
![]() $p_0+1$
many new points between the y points,
$p_0+1$
many new points between the y points,
![]() $xy$
and
$xy$
and
![]() $yx$
as indicated above. This becomes
$yx$
as indicated above. This becomes
![]() $B_0[s_0+1]$
, and naturally also involves making all the blocks
$B_0[s_0+1]$
, and naturally also involves making all the blocks
![]() $B_j[s_0+1]$
(
$B_j[s_0+1]$
(
![]() $j> 0$
) bigger to keep the strong
$j> 0$
) bigger to keep the strong
![]() $\eta $
-representation property. (For instance, add
$\eta $
-representation property. (For instance, add
![]() $|B_0[s_0]|+2p_0+2$
many points to their right ends).
$|B_0[s_0]|+2p_0+2$
many points to their right ends).
The point of this is the following. If
![]() $W_0$
is to be isomorphic to
$W_0$
is to be isomorphic to
![]() $\mathcal {L}$
, then
$\mathcal {L}$
, then
![]() $B_0[s_0+1]$
needs an image. But
$B_0[s_0+1]$
needs an image. But
![]() $Z_0[s_0]$
needs a pre-image. There are no blocks in
$Z_0[s_0]$
needs a pre-image. There are no blocks in
![]() $\mathcal {L}$
left of
$\mathcal {L}$
left of
![]() $B_0[s_0+1]$
. So the pre-image must either be
$B_0[s_0+1]$
. So the pre-image must either be
![]() $B_0[s_0+1]$
, or something right of this block. Thus, the image of
$B_0[s_0+1]$
, or something right of this block. Thus, the image of
![]() $B_0[s_0+1]$
cannot contain
$B_0[s_0+1]$
cannot contain
![]() $z_0$
.
$z_0$
.
We conclude that in either cases, the pre-image of
![]() $z_0$
must be in a block
$z_0$
must be in a block
![]() $B_{j}[s]$
for
$B_{j}[s]$
for
![]() $j> 0$
at some
$j> 0$
at some
![]() $s> s_0$
.
$s> s_0$
.
Case 3. Now we will again wait for a stage
![]() $s_1>s_0$
such that
$s_1>s_0$
such that
![]() $\varphi _{0}^{\emptyset '}(x,\, s_1) = z_0[s_1]$
, and the
$\varphi _{0}^{\emptyset '}(x,\, s_1) = z_0[s_1]$
, and the
![]() $\varphi _{0}^{\emptyset '}[s_1]$
to seem correct, meaning that
$\varphi _{0}^{\emptyset '}[s_1]$
to seem correct, meaning that
![]() $Z_0[s_1]$
must be a
$Z_0[s_1]$
must be a
![]() $\emptyset '$
-guaranteed block of size
$\emptyset '$
-guaranteed block of size
![]() $|B_j [s_1]|$
where
$|B_j [s_1]|$
where
![]() $x\in B_j[s_1]$
, of course, for some
$x\in B_j[s_1]$
, of course, for some
![]() $j>0$
. Our action is similarly to the above.
$j>0$
. Our action is similarly to the above.
First, between
![]() $B_{j-1}[s_1]$
and
$B_{j-1}[s_1]$
and
![]() $B_j [s_1]$
we begin a new block
$B_j [s_1]$
we begin a new block
![]() $B_j [s_1 + 1]$
, by first increasing the size of
$B_j [s_1 + 1]$
, by first increasing the size of
![]() $B_k[s_1]$
for
$B_k[s_1]$
for
![]() $k\geq j$
, waiting for
$k\geq j$
, waiting for
![]() $\varphi _{0}^{\emptyset '}$
to catch up and then beginning the new block, for instance, of the same size as
$\varphi _{0}^{\emptyset '}$
to catch up and then beginning the new block, for instance, of the same size as
![]() $B_j [s_1]$
, noting that
$B_j [s_1]$
, noting that
![]() $B_{j+1} [s_1+1] = B_{j}[s_1]$
once this has begun. Now we will repeat the argument with the blocks
$B_{j+1} [s_1+1] = B_{j}[s_1]$
once this has begun. Now we will repeat the argument with the blocks
![]() $B_j [s_1]$
and
$B_j [s_1]$
and
![]() $B_{j+1}[s_1 + 1]$
.
$B_{j+1}[s_1 + 1]$
.
That is, we’d wait for
![]() $\varphi _{0}^{\emptyset '}[s_2]$
to look like a partial isomorphism on these two blocks giving images
$\varphi _{0}^{\emptyset '}[s_2]$
to look like a partial isomorphism on these two blocks giving images
![]() $Z_j [s_2]$
and
$Z_j [s_2]$
and
![]() $Z = Z_{j+1}[s_2]$
, say at stage
$Z = Z_{j+1}[s_2]$
, say at stage
![]() $s_2>s_1$
. We’d if there are at least
$s_2>s_1$
. We’d if there are at least
![]() $2p_2 + 2$
many points between them in
$2p_2 + 2$
many points between them in
![]() $W_0$
. In the case that there are not we promise to densify between
$W_0$
. In the case that there are not we promise to densify between
![]() $B_j [s_2]$
and
$B_j [s_2]$
and
![]() $B_{j+1}[s_2 + 1]$
, and note that the blocks
$B_{j+1}[s_2 + 1]$
, and note that the blocks
![]() $Z_j [s_2]$
and
$Z_j [s_2]$
and
![]() $Z = Z_{j+1}[s_2]$
become amalgamated in
$Z = Z_{j+1}[s_2]$
become amalgamated in
![]() $W_0$
and their pre-image must be right of
$W_0$
and their pre-image must be right of
![]() $B_{j+1}[s_2 + 1]$
. If there are many such points, we would amalgamate
$B_{j+1}[s_2 + 1]$
. If there are many such points, we would amalgamate
![]() $B_j [s_2]$
and
$B_j [s_2]$
and
![]() $B_{j+1}[s_2]$
to make
$B_{j+1}[s_2]$
to make
![]() $B_j [s_2+1]$
; and again this forces the pre-image of
$B_j [s_2+1]$
; and again this forces the pre-image of
![]() $Z_s$
right of
$Z_s$
right of
![]() $B_j [s]$
for all
$B_j [s]$
for all
![]() $s> s_2$
.
$s> s_2$
.
Now if this cycle happens infinitely often, Z cannot have a pre-image (outcome
![]() $\mathbf {0}$
, and
$\mathbf {0}$
, and
![]() $Z_s \to \infty $
). If it does not (outcome
$Z_s \to \infty $
). If it does not (outcome
![]() $\mathbf {1}$
) then
$\mathbf {1}$
) then
![]() $\varphi _{0}^{\emptyset '}[s]$
stops recovering. In either case,
$\varphi _{0}^{\emptyset '}[s]$
stops recovering. In either case,
![]() $\varphi _{0}^{\emptyset "}$
is not an isomorphism.
$\varphi _{0}^{\emptyset "}$
is not an isomorphism.
The reader can see that this strategy has two outcomes
![]() $\mathbf {0} <_L \mathbf {1}$
, i.e., outcome
$\mathbf {0} <_L \mathbf {1}$
, i.e., outcome
![]() $\mathbf {0}$
is the true outcome if and only if it happens infinitely many time. The general strategies will follow a reasonably standard
$\mathbf {0}$
is the true outcome if and only if it happens infinitely many time. The general strategies will follow a reasonably standard
![]() $\Pi ^0_2$
-argument. For example,
$\Pi ^0_2$
-argument. For example,
![]() $P_0$
will have one version
$P_0$
will have one version
![]() $R_{\varepsilon }$
, and
$R_{\varepsilon }$
, and
![]() $P_1$
will have two versions
$P_1$
will have two versions
![]() $R_0$
and
$R_0$
and
![]() $R_1$
, and
$R_1$
, and
![]() $P_2$
will have four versions
$P_2$
will have four versions
![]() $R_{00}$
,
$R_{00}$
,
![]() $R_{01}$
,
$R_{01}$
,
![]() $R_{10}$
,
$R_{10}$
,
![]() $R_{11}$
, and so on.
$R_{11}$
, and so on.
![]() $R_1$
simply works with two blocks right of the current two blocks being used by
$R_1$
simply works with two blocks right of the current two blocks being used by
![]() $R_{\varepsilon }$
. It is initialized each time
$R_{\varepsilon }$
. It is initialized each time
![]() $R_{\varepsilon }$
acts.
$R_{\varepsilon }$
acts.
![]() $R_0$
is aware of the fact that
$R_0$
is aware of the fact that
![]() $R_{\varepsilon }$
will cause Z to become infinite, and will use pairs of blocks
$R_{\varepsilon }$
will cause Z to become infinite, and will use pairs of blocks
![]() $B_j$
,
$B_j$
,
![]() $B_{j+1}[s]$
with
$B_{j+1}[s]$
with
![]() $j\to \infty $
. It’s strategy is obvious. It will use blocks left of those being used by
$j\to \infty $
. It’s strategy is obvious. It will use blocks left of those being used by
![]() $R_{\varepsilon }$
. It waits for the pre-image of
$R_{\varepsilon }$
. It waits for the pre-image of
![]() $z_0$
to be in some
$z_0$
to be in some
![]() $B_j$
for
$B_j$
for
![]() $j> 3 $
. (In general
$j> 3 $
. (In general
![]() $P_e$
will pick a base be large enough that a single block can only be used by finitely many strategies. This makes sure that all blocks are finite.)
$P_e$
will pick a base be large enough that a single block can only be used by finitely many strategies. This makes sure that all blocks are finite.)
![]() $R_0$
would then use
$R_0$
would then use
![]() $B_1[s]$
and
$B_1[s]$
and
![]() $B_2[s]$
as its base blocks, and looking for an image of the first element of
$B_2[s]$
as its base blocks, and looking for an image of the first element of
![]() $B_2[s]$
to be
$B_2[s]$
to be
![]() $z_1$
. The reader should also note that if we wish to increase the size of a block
$z_1$
. The reader should also note that if we wish to increase the size of a block
![]() $B_k$
for the sake of
$B_k$
for the sake of
![]() $R_0$
, then we would first do it, wait for
$R_0$
, then we would first do it, wait for
![]() $\varphi ^{\emptyset '}_0$
to recover first before looking at
$\varphi ^{\emptyset '}_0$
to recover first before looking at
![]() $\varphi ^{\emptyset '}_1$
. In general, once we force
$\varphi ^{\emptyset '}_1$
. In general, once we force
![]() $(\varphi ^{\emptyset '}_1)^{-1}(z_1)$
to move right of
$(\varphi ^{\emptyset '}_1)^{-1}(z_1)$
to move right of
![]() $B_1$
, before we’d attack
$B_1$
, before we’d attack
![]() $R_0$
again, we’d wait for
$R_0$
again, we’d wait for
![]() $R_{\varepsilon }$
to be strictly right of the relevant attack blocks in
$R_{\varepsilon }$
to be strictly right of the relevant attack blocks in
![]() $\mathcal {L}$
. This action requires accuracy, which is detailed in the formal part of the proof.
$\mathcal {L}$
. This action requires accuracy, which is detailed in the formal part of the proof.
The inductive strategies are straightforward extensions of the above.
3 The formal construction
As explained in the previous section, the formal construction consists of three parts. We give, initially, the strategy
![]() $\mathcal {L}$
of the construction of the linear order, secondly, strategies
$\mathcal {L}$
of the construction of the linear order, secondly, strategies
![]() $R_{\sigma }$
of a requirement
$R_{\sigma }$
of a requirement
![]() $P_e$
, where
$P_e$
, where
![]() $|\sigma |=e$
, and, finally, the general strategy which controls the execution of other strategies.
$|\sigma |=e$
, and, finally, the general strategy which controls the execution of other strategies.
From now, we fix the oracle
![]() $\emptyset '$
until the end of the proof.
$\emptyset '$
until the end of the proof.
3.1 The strategy
 $\mathcal {L}$
$\mathcal {L}$
This strategy describes the construction of the linear order due to the parameters defined by strategies
![]() $R_\sigma $
. We will construct a sequence of
$R_\sigma $
. We will construct a sequence of
![]() ${\emptyset '}$
-computable linear orders
${\emptyset '}$
-computable linear orders
![]() $\mathcal {L}_s$
with
$\mathcal {L}_s$
with
![]() ${\emptyset '}$
-computable successor relations
${\emptyset '}$
-computable successor relations
![]() $S_{\mathcal {L}_s}$
such that
$S_{\mathcal {L}_s}$
such that
![]() $\mathcal {L}_s\subseteq \mathcal {L}_{s+1}$
,
$\mathcal {L}_s\subseteq \mathcal {L}_{s+1}$
,
![]() $S_{\mathcal {L}_s}\subseteq \mathcal {L}_{s+1}$
,
$S_{\mathcal {L}_s}\subseteq \mathcal {L}_{s+1}$
,
![]() $\mathcal {L}=\bigcup \limits _{s\in \omega }\mathcal {L}_s$
, and
$\mathcal {L}=\bigcup \limits _{s\in \omega }\mathcal {L}_s$
, and
![]() $S_{\mathcal {L}}=\bigcup \limits _{s\in \omega }S_{\mathcal {L}_s}$
. Since
$S_{\mathcal {L}}=\bigcup \limits _{s\in \omega }S_{\mathcal {L}_s}$
. Since
![]() $S_{\mathcal {L}_s}\subseteq S_{\mathcal {L}_{s+1}}$
, we will use S instead of
$S_{\mathcal {L}_s}\subseteq S_{\mathcal {L}_{s+1}}$
, we will use S instead of
![]() $S_{\mathcal {L}_s}$
. It will not cause of misunderstandings. The successor relation on
$S_{\mathcal {L}_s}$
. It will not cause of misunderstandings. The successor relation on
![]() $W_e$
is denoted by
$W_e$
is denoted by
![]() $S_e$
. We will use the following notations:
$S_e$
. We will use the following notations:
![]() $<$
is a standard order on natural numbers,
$<$
is a standard order on natural numbers,
![]() $<_{\mathcal {L}}$
is the constructed linear order, and
$<_{\mathcal {L}}$
is the constructed linear order, and
![]() $<_e$
is the order on
$<_e$
is the order on
![]() $W_e$
.
$W_e$
.
Moreover, in the during of the construction we will define a predicate
![]() $P(u,v,e,s)$
which is a protection of the requirement with the number e to add new elements between u and v at stage s.
$P(u,v,e,s)$
which is a protection of the requirement with the number e to add new elements between u and v at stage s.
Stage
![]() $0$
. We define
$0$
. We define
![]() $\mathcal {L}_0=\{0\}$
.
$\mathcal {L}_0=\{0\}$
.
Stage
![]() $s+1$
. For every pair of elements
$s+1$
. For every pair of elements
![]() $u<_{\mathcal {L}}v<_{\mathcal {L}}2{s+1}$
from
$u<_{\mathcal {L}}v<_{\mathcal {L}}2{s+1}$
from
![]() $L_{s}$
such that
$L_{s}$
such that
![]() $\neg S(u,v)$
and
$\neg S(u,v)$
and
![]() $(\forall \sigma )[ (|\sigma |\leq s+1)\&\neg P(u,\,v,\,\sigma ,\,s+1)]$
(i.e., they are not protected by a higher priority strategy), we add one new element between u and v.
$(\forall \sigma )[ (|\sigma |\leq s+1)\&\neg P(u,\,v,\,\sigma ,\,s+1)]$
(i.e., they are not protected by a higher priority strategy), we add one new element between u and v.
We add into
![]() $\mathcal {L}_{s+1}$
the least unused odd number as the least element, and the least unused even number a as the greatest element. Let k be the greatest size of
$\mathcal {L}_{s+1}$
the least unused odd number as the least element, and the least unused even number a as the greatest element. Let k be the greatest size of
![]() $\mathcal {L}_s$
-blocks. Then we choose the least odd numbers such that
$\mathcal {L}_s$
-blocks. Then we choose the least odd numbers such that
![]() $u_1,\,\ldots ,\, u_{2k}\notin L_s$
. We put them into
$u_1,\,\ldots ,\, u_{2k}\notin L_s$
. We put them into
![]() $\mathcal {L}_{s+1}$
and define
$\mathcal {L}_{s+1}$
and define
![]() $a<_{\mathcal {L}}u_1<_{\mathcal {L}}\cdots <_{\mathcal {L}}u_{2k}$
,
$a<_{\mathcal {L}}u_1<_{\mathcal {L}}\cdots <_{\mathcal {L}}u_{2k}$
,
![]() $S(a,u_1)$
, and
$S(a,u_1)$
, and
![]() $S(u_i,\,u_{i+1})$
for all
$S(u_i,\,u_{i+1})$
for all
![]() $i={1,\,\ldots ,\,2k}$
.
$i={1,\,\ldots ,\,2k}$
.
For every pair of elements
![]() $u,v\in L_{s+1}$
such that the relation
$u,v\in L_{s+1}$
such that the relation
![]() $S(u,v)$
is not defined, we set
$S(u,v)$
is not defined, we set
![]() $\neg S(u,v)$
. This completes the description of the strategy
$\neg S(u,v)$
. This completes the description of the strategy
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
3.2 The tree of strategies
We will use
![]() $\sigma , \tau , \mu $
to denote finite or infinite binary strings. The empty string we denoted by
$\sigma , \tau , \mu $
to denote finite or infinite binary strings. The empty string we denoted by
![]() $\varepsilon $
. If
$\varepsilon $
. If
![]() $\sigma =t_1t_2t_3\ldots $
is a finite or infinite string then
$\sigma =t_1t_2t_3\ldots $
is a finite or infinite string then
![]() $\sigma (i)=t_i$
,
$\sigma (i)=t_i$
,
![]() $\sigma \upharpoonright 0=\varepsilon $
, and
$\sigma \upharpoonright 0=\varepsilon $
, and
![]() $\sigma \upharpoonright i=t_1\ldots t_i$
. If
$\sigma \upharpoonright i=t_1\ldots t_i$
. If
![]() $\sigma $
and
$\sigma $
and
![]() $\mu $
are finite strings then the concatenation of these strings we denoted by
$\mu $
are finite strings then the concatenation of these strings we denoted by
![]() $\sigma \mu $
. The length of the finite string
$\sigma \mu $
. The length of the finite string
![]() $\sigma $
is denoted by
$\sigma $
is denoted by
![]() $|\sigma |$
. If A is a set then
$|\sigma |$
. If A is a set then
![]() $|A|$
denotes the cardinality of the set.
$|A|$
denotes the cardinality of the set.
For every finite binary string
![]() $\sigma $
, we describe a strategy
$\sigma $
, we describe a strategy
![]() $R_\sigma $
. Every strategy
$R_\sigma $
. Every strategy
![]() $R_\sigma $
has two outcomes:
$R_\sigma $
has two outcomes:
-
 $\mathbf {0}$
—the pre-image of a witness
$\mathbf {0}$
—the pre-image of a witness
 $y_\sigma $
has changed infinitely often;
$y_\sigma $
has changed infinitely often; -
 $\mathbf {1}$
—the isomorphism
$\mathbf {1}$
—the isomorphism
 $\varphi _e^{\emptyset "}$
is diagonalized using finitely many stages.
$\varphi _e^{\emptyset "}$
is diagonalized using finitely many stages.
A strategy
![]() $R_\sigma $
tries to satisfy the requirement
$R_\sigma $
tries to satisfy the requirement
![]() $P_e$
, where
$P_e$
, where
![]() $e=|\sigma |$
. This strategy uses the assumption that for every
$e=|\sigma |$
. This strategy uses the assumption that for every
![]() $i<|\sigma |$
the strategy
$i<|\sigma |$
the strategy
![]() $R_{\sigma \upharpoonright i}$
has the true outcome
$R_{\sigma \upharpoonright i}$
has the true outcome
![]() $\sigma (i)$
. Thus, the set of strategies
$\sigma (i)$
. Thus, the set of strategies
![]() $R_\sigma $
is located on a binary tree. To be specific, the left branch of the tree corresponds to the outcome
$R_\sigma $
is located on a binary tree. To be specific, the left branch of the tree corresponds to the outcome
![]() $\mathbf {0}$
, and the right branch corresponds to the outcome
$\mathbf {0}$
, and the right branch corresponds to the outcome
![]() $\mathbf {1}$
. Note that there are
$\mathbf {1}$
. Note that there are
![]() $2^e$
strategies
$2^e$
strategies
![]() $R_\sigma $
such that
$R_\sigma $
such that
![]() $e=|\sigma |$
which try to satisfy requirement
$e=|\sigma |$
which try to satisfy requirement
![]() $P_e$
. Let’s move on to the detailed description of strategies
$P_e$
. Let’s move on to the detailed description of strategies
![]() $R_\sigma $
.
$R_\sigma $
.
3.3 The strategy
 $R_\sigma $
$R_\sigma $
Since we already fixed the oracle
![]() $\emptyset '$
, we will use
$\emptyset '$
, we will use
![]() $\varphi _e$
instead of
$\varphi _e$
instead of
![]() $\varphi ^{\emptyset '}_e$
to simplified notations.
$\varphi ^{\emptyset '}_e$
to simplified notations.
Stage
![]() $0$
. We initialize the strategy
$0$
. We initialize the strategy
![]() $R_{\sigma }$
. Hereinafter, this means that we define
$R_{\sigma }$
. Hereinafter, this means that we define
![]() $w_{\sigma }[0]=0$
and set the witness
$w_{\sigma }[0]=0$
and set the witness
![]() $y_{\sigma }[0]$
and the parameters
$y_{\sigma }[0]$
and the parameters
![]() $x_{\sigma }[0]$
and
$x_{\sigma }[0]$
and
![]() $d_{\sigma }[0]$
are undefined.
$d_{\sigma }[0]$
are undefined.
Stage
![]() $s+1$
. There are three cases. In the first case, the witness
$s+1$
. There are three cases. In the first case, the witness
![]() $y_\sigma [s]$
is undefined. In the second case,
$y_\sigma [s]$
is undefined. In the second case,
![]() $y_\sigma [s]$
is defined, but
$y_\sigma [s]$
is defined, but
![]() $x_\sigma [s]$
is undefined. And in the third case, both
$x_\sigma [s]$
is undefined. And in the third case, both
![]() $y_\sigma [s]$
and
$y_\sigma [s]$
and
![]() $x_\sigma [s]$
are defined.
$x_\sigma [s]$
are defined.
Case 1. The witness
![]() $y_\sigma [s]$
is undefined. It is possible that either the strategy does not choose a witness or the work of the strategy is injured by a higher priority strategy.
$y_\sigma [s]$
is undefined. It is possible that either the strategy does not choose a witness or the work of the strategy is injured by a higher priority strategy.
We check the existence of two non-singleton blocks
![]() $B_{l}=[l_{l},\,l_{r}]_s$
and
$B_{l}=[l_{l},\,l_{r}]_s$
and
![]() $B_{r}=[r_{l},\,r_{r}]_s$
of
$B_{r}=[r_{l},\,r_{r}]_s$
of
![]() $\mathcal {L}_s$
such that:
$\mathcal {L}_s$
such that:
1.1 These blocks are adjacent at this stage, i.e.,
![]() $(\forall u,\,v\in \mathcal {L}_s)[u,\,v\in [l_{r},\,r_{l}]_s\rightarrow \neg S(u,v)]$
.
$(\forall u,\,v\in \mathcal {L}_s)[u,\,v\in [l_{r},\,r_{l}]_s\rightarrow \neg S(u,v)]$
.
1.2
![]() $\varphi _e(\cdot ,s+1)$
is correctly defined on
$\varphi _e(\cdot ,s+1)$
is correctly defined on
![]() $B^\leq _{r}=\{u \in L_s\mid u\leq _{\mathcal {L}} r_r \,\&\, (\exists v\in L_s)\, [S(u,\,v)]\}$
, i.e.,
$B^\leq _{r}=\{u \in L_s\mid u\leq _{\mathcal {L}} r_r \,\&\, (\exists v\in L_s)\, [S(u,\,v)]\}$
, i.e.,
![]() $B^\leq _{r}$
is the set of elements belong to non-singleton blocks to the left of
$B^\leq _{r}$
is the set of elements belong to non-singleton blocks to the left of
![]() $B_r$
and belong to
$B_r$
and belong to
![]() $B_r$
. Correct definiteness means that:
$B_r$
. Correct definiteness means that:
1.2.1
![]() $\varphi _e(\cdot ,s+1)$
is order preserving on
$\varphi _e(\cdot ,s+1)$
is order preserving on
![]() $B^\leq _{r}$
, i.e., for all
$B^\leq _{r}$
, i.e., for all
![]() $u,\,v\in B^\leq _{r}$
, if
$u,\,v\in B^\leq _{r}$
, if
![]() $u<_{\mathcal {L}}v$
then
$u<_{\mathcal {L}}v$
then
![]() $\varphi _e(u,s+1)<_e\varphi _e(v,s+1)$
.
$\varphi _e(u,s+1)<_e\varphi _e(v,s+1)$
.
1.2.2
![]() $\varphi _e(\cdot ,s+1)$
preserves the successor relation, i.e., for all
$\varphi _e(\cdot ,s+1)$
preserves the successor relation, i.e., for all
![]() $u,\,v\in B^\leq _{r}$
, if
$u,\,v\in B^\leq _{r}$
, if
![]() $S(u,v)$
then
$S(u,v)$
then
![]() $S_e(\varphi _e(u,s+1),\varphi _e(v,s+1))$
.
$S_e(\varphi _e(u,s+1),\varphi _e(v,s+1))$
.
1.2.3
![]() $\varphi _e(\cdot ,s+1)$
preserves right and left ends of blocks, i.e., for all
$\varphi _e(\cdot ,s+1)$
preserves right and left ends of blocks, i.e., for all
![]() $u\in B^\leq _{r}$
, if
$u\in B^\leq _{r}$
, if
![]() $\neg (\exists v\in L_s)\,[v>_{\mathcal {L}}u\,\&\, S(u,\,v)]$
then
$\neg (\exists v\in L_s)\,[v>_{\mathcal {L}}u\,\&\, S(u,\,v)]$
then
and, similarly, if
![]() $\neg (\exists v\in L_s)\,[v<_{\mathcal {L}}u\,\&\, S(u,\,v)]$
then
$\neg (\exists v\in L_s)\,[v<_{\mathcal {L}}u\,\&\, S(u,\,v)]$
then
Note that from the points above it follows that the blocks of
![]() $\mathcal {L}_s$
map to blocks of
$\mathcal {L}_s$
map to blocks of
![]() $W_{e,s+1}$
under
$W_{e,s+1}$
under
![]() $\varphi _e(\cdot ,s+1)$
.
$\varphi _e(\cdot ,s+1)$
.
1.3 The location of the blocks
![]() $B_{l}$
and
$B_{l}$
and
![]() $B_{r}$
is consistent with higher priority strategies. Namely, for all
$B_{r}$
is consistent with higher priority strategies. Namely, for all
![]() $i<|\sigma |$
, if
$i<|\sigma |$
, if
![]() $\sigma (i)=1$
then
$\sigma (i)=1$
then
![]() $B_{r,\,\sigma \upharpoonright i}<_{\mathcal {L}}B_{l}<_{\mathcal {L}} B_{r}$
, and if
$B_{r,\,\sigma \upharpoonright i}<_{\mathcal {L}}B_{l}<_{\mathcal {L}} B_{r}$
, and if
![]() $\sigma (i)=0$
then
$\sigma (i)=0$
then
![]() $B_{l}<_{\mathcal {L}} B_{r}<_{\mathcal {L}} B_{l,\,\sigma \upharpoonright i}$
.
$B_{l}<_{\mathcal {L}} B_{r}<_{\mathcal {L}} B_{l,\,\sigma \upharpoonright i}$
.
1.4 The least even number belongs to
![]() $B_l\cup B_r$
is bigger than
$B_l\cup B_r$
is bigger than
![]() $2e$
.
$2e$
.
If the blocks
![]() $B_{l}$
and
$B_{l}$
and
![]() $B_{r}$
satisfying the conditions above exist, then there are three possibilities:
$B_{r}$
satisfying the conditions above exist, then there are three possibilities:
a)
![]() $\!B_l$
contains an even number;
$\!B_l$
contains an even number;
![]() $B_r$
does not contain an even number.
$B_r$
does not contain an even number.
b)
![]() $\!B_r$
contains an even number;
$\!B_r$
contains an even number;
![]() $B_l$
does not contain an even number.
$B_l$
does not contain an even number.
c) Both
![]() $B_l$
and
$B_l$
and
![]() $B_r$
contain even numbers.
$B_r$
contain even numbers.
In cases (a) and (b) we define
![]() $B_{l,\,\sigma }[s+1]=B_l$
,
$B_{l,\,\sigma }[s+1]=B_l$
,
![]() $B_{r,\,\sigma }[s+1]=B_r$
,
$B_{r,\,\sigma }[s+1]=B_r$
,
![]() $l_{l,\,\sigma }[s+1]=l_{l}$
,
$l_{l,\,\sigma }[s+1]=l_{l}$
,
![]() $l_{r,\,\sigma }[s+1]=l_{r}$
,
$l_{r,\,\sigma }[s+1]=l_{r}$
,
![]() $r_{l,\,\sigma }[s+1]=r_{l}$
,
$r_{l,\,\sigma }[s+1]=r_{l}$
,
![]() $r_{r,\,\sigma }[s+1]=\,r_{r}$
,
$r_{r,\,\sigma }[s+1]=\,r_{r}$
,
![]() $P(l_{r,\,\sigma },\, r_{l,\,\sigma },\,\sigma ,\,s+1)=1$
,
$P(l_{r,\,\sigma },\, r_{l,\,\sigma },\,\sigma ,\,s+1)=1$
,
![]() $w_\sigma [s+1]=0$
, and
$w_\sigma [s+1]=0$
, and
![]() $d_\sigma [s+1]=\min \{k\mid 2k \in B_l\cup B_r \}$
.
$d_\sigma [s+1]=\min \{k\mid 2k \in B_l\cup B_r \}$
.
In case (c) we have
![]() $|B_l|<|B_r|$
. Recall that all blocks with even numbers have even sizes. Consequently, both the numbers
$|B_l|<|B_r|$
. Recall that all blocks with even numbers have even sizes. Consequently, both the numbers
![]() $|B_l|$
and
$|B_l|$
and
![]() $|B_r|$
are even and, therefore,
$|B_r|$
are even and, therefore,
![]() $|B_l|<|B_l|+1<|B_r|$
. We add a new block
$|B_l|<|B_l|+1<|B_r|$
. We add a new block
![]() $B'=[l',\,r']$
between
$B'=[l',\,r']$
between
![]() $B_l$
and
$B_l$
and
![]() $B_r$
such that the new block consists of
$B_r$
such that the new block consists of
![]() $|B_l|+1$
odd numbers. We define
$|B_l|+1$
odd numbers. We define
![]() $B_{l,\,\sigma }[s+1]=B'$
,
$B_{l,\,\sigma }[s+1]=B'$
,
![]() $B_{r,\,\sigma }[s+1]=B_r$
,
$B_{r,\,\sigma }[s+1]=B_r$
,
![]() $l_{l,\,\sigma }[s+1]=l'$
,
$l_{l,\,\sigma }[s+1]=l'$
,
![]() $l_{r,\,\sigma }[s+1]=r'$
,
$l_{r,\,\sigma }[s+1]=r'$
,
![]() $x_{\sigma }[s+1]=r_{l,\,\sigma }[s+1]=r_l$
,
$x_{\sigma }[s+1]=r_{l,\,\sigma }[s+1]=r_l$
,
![]() $y_\sigma [s+1]=\varphi _e(x_\sigma [s+1],\,s+1)$
,
$y_\sigma [s+1]=\varphi _e(x_\sigma [s+1],\,s+1)$
,
![]() $r_{r,\,\sigma }[s+1]=\,r_{r}$
,
$r_{r,\,\sigma }[s+1]=\,r_{r}$
,
![]() $P(l_{r,\,\sigma }[s+1],\, r_{l,\,\sigma }[s+1],\,\sigma , s+1)=1$
,
$P(l_{r,\,\sigma }[s+1],\, r_{l,\,\sigma }[s+1],\,\sigma , s+1)=1$
,
![]() $w_\sigma [s+1]=0$
, and
$w_\sigma [s+1]=0$
, and
![]() $d_\sigma [s+1]=\min \{k\mid 2k \in B_l\cup B_r \}.$
$d_\sigma [s+1]=\min \{k\mid 2k \in B_l\cup B_r \}.$
If no blocks are satisfying the conditions 1.1–1.4 then
![]() $x_\sigma [s+1]$
and
$x_\sigma [s+1]$
and
![]() $y_\sigma [s+1]$
are still undefined. In both the cases, the outcome of the strategy is
$y_\sigma [s+1]$
are still undefined. In both the cases, the outcome of the strategy is
![]() $\mathbf {1}$
.
$\mathbf {1}$
.
Case 2. Both the parameters
![]() $y_\sigma [s]$
and
$y_\sigma [s]$
and
![]() $x_\sigma [s]$
are defined. There are the following subcases: Case 2.1 means that the approximation of the isomorphism looks incorrect, and Cases 2.2–2.4 mean that the approximation of the isomorphism looks correct with additional conditions.
$x_\sigma [s]$
are defined. There are the following subcases: Case 2.1 means that the approximation of the isomorphism looks incorrect, and Cases 2.2–2.4 mean that the approximation of the isomorphism looks correct with additional conditions.
Case 2.1. The approximation of the isomorphism looks incorrect, i.e., at least one of the conditions of 1.2 does not hold. Then we take off protection, which was established by this strategy, to add new elements into
![]() $\mathcal {L}$
between
$\mathcal {L}$
between
![]() $l_{r,\,\sigma }[s]$
and
$l_{r,\,\sigma }[s]$
and
![]() $r_{l,\,\sigma }[s]$
, i.e., we define
$r_{l,\,\sigma }[s]$
, i.e., we define
![]() $P(l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s],\,\sigma ,\,s+1)=0$
. The outcome of the strategy is
$P(l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s],\,\sigma ,\,s+1)=0$
. The outcome of the strategy is
![]() $\mathbf {1}$
.
$\mathbf {1}$
.
Further, assume that Case 2.1 does not hold, i.e., the approximation of the isomorphism looks correct (all the conditions of 1.2 hold).
Case 2.2. Assume that
![]() $\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)= x_\sigma [s]$
and
$\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)= x_\sigma [s]$
and
![]() $|[\varphi _e(l_{r,\,\sigma }[s],\,s+1), \varphi _e(r_{l,\,\sigma }[s],\,s+1)]|\leq 2|[l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s]]_s|+1$
, i.e.,
$|[\varphi _e(l_{r,\,\sigma }[s],\,s+1), \varphi _e(r_{l,\,\sigma }[s],\,s+1)]|\leq 2|[l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s]]_s|+1$
, i.e.,
![]() $W_e$
has no between the images of
$W_e$
has no between the images of
![]() $B_{l,\,\sigma }[s]$
and
$B_{l,\,\sigma }[s]$
and
![]() $B_{r,\,\sigma }[s]$
two times plus one more elements than
$B_{r,\,\sigma }[s]$
two times plus one more elements than
![]() $\mathcal {L}_s$
has enumerated between blocks
$\mathcal {L}_s$
has enumerated between blocks
![]() $B_{l,\,\sigma }[s]$
and
$B_{l,\,\sigma }[s]$
and
![]() $B_{r,\,\sigma }[s]$
. Then we define
$B_{r,\,\sigma }[s]$
. Then we define
![]() $P(l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s],\,\sigma ,\,s+1)=1$
and the outcome is
$P(l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s],\,\sigma ,\,s+1)=1$
and the outcome is
![]() $1$
.
$1$
.
Case 2.3. Assume that
![]() $\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)= x_\sigma [s]$
and
$\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)= x_\sigma [s]$
and
![]() $|[\varphi _e(l_{r,\,\sigma }[s],\,s+1), \varphi _e(r_{l,\,\sigma }[s],\,s+1)]|>2|[l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s]]_s|+1$
, i.e.,
$|[\varphi _e(l_{r,\,\sigma }[s],\,s+1), \varphi _e(r_{l,\,\sigma }[s],\,s+1)]|>2|[l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s]]_s|+1$
, i.e.,
![]() $W_e$
has between the images of
$W_e$
has between the images of
![]() $B_{l,\,\sigma }[s]$
and
$B_{l,\,\sigma }[s]$
and
![]() $B_{r,\,\sigma }[s]$
two times plus one more elements than
$B_{r,\,\sigma }[s]$
two times plus one more elements than
![]() $\mathcal {L}_s$
has enumerated between the blocks
$\mathcal {L}_s$
has enumerated between the blocks
![]() $B_{l,\,\sigma }[s]$
and
$B_{l,\,\sigma }[s]$
and
![]() $B_{r,\,\sigma }[s]$
. In this case, we amalgamate the blocks
$B_{r,\,\sigma }[s]$
. In this case, we amalgamate the blocks
![]() $B_{l,\,\sigma }[s]$
and
$B_{l,\,\sigma }[s]$
and
![]() $B_{r,\,\sigma }[s]$
. To this purpose, we do the following procedure.
$B_{r,\,\sigma }[s]$
. To this purpose, we do the following procedure.
If
![]() $[l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s]]_s=\{u_0<_{\mathcal {L}}u_1<_{\mathcal {L}}\cdots <_{\mathcal {L}}u_{m+1}\}$
, then we choose the least unused odd numbers
$[l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s]]_s=\{u_0<_{\mathcal {L}}u_1<_{\mathcal {L}}\cdots <_{\mathcal {L}}u_{m+1}\}$
, then we choose the least unused odd numbers
![]() $v_0,\,\ldots ,\, v_m$
and define
$v_0,\,\ldots ,\, v_m$
and define
![]() $u_i<_{\mathcal {L}}v_i<_{\mathcal {L}}u_{i+1}$
. If the number of elements between
$u_i<_{\mathcal {L}}v_i<_{\mathcal {L}}u_{i+1}$
. If the number of elements between
![]() $l_{l,\,\sigma }[s]$
and
$l_{l,\,\sigma }[s]$
and
![]() $r_{r,\,\sigma }[s]$
is odd, then we choose one more the least unused odd number
$r_{r,\,\sigma }[s]$
is odd, then we choose one more the least unused odd number
![]() $v_{-1}$
and define
$v_{-1}$
and define
![]() $u_0<_{\mathcal {L}}v_{-1}<_{\mathcal {L}}v_{0}$
,
$u_0<_{\mathcal {L}}v_{-1}<_{\mathcal {L}}v_{0}$
,
![]() $S(u_0,\,v_{-1})$
,
$S(u_0,\,v_{-1})$
,
![]() $S(v_{-1},\,v_0)$
, and
$S(v_{-1},\,v_0)$
, and
![]() $S(v_0,\,u_1)$
. Otherwise, if the number of elements between
$S(v_0,\,u_1)$
. Otherwise, if the number of elements between
![]() $l_{l,\,\sigma }[s]$
and
$l_{l,\,\sigma }[s]$
and
![]() $r_{r,\,\sigma }[s]$
is even, then we define
$r_{r,\,\sigma }[s]$
is even, then we define
![]() $S(u_0,\,v_{0})$
and
$S(u_0,\,v_{0})$
and
![]() $S(v_0,\,u_1)$
. For all other
$S(v_0,\,u_1)$
. For all other
![]() $i\in \{1,\,\ldots ,\,m\}$
, we define
$i\in \{1,\,\ldots ,\,m\}$
, we define
![]() $S(u_i,\,v_i)$
and
$S(u_i,\,v_i)$
and
![]() $S(v_i,\,u_{i+1})$
. Thus, the amalgamated block
$S(v_i,\,u_{i+1})$
. Thus, the amalgamated block
![]() $[l_{l,\,\sigma }[s],\,r_{r,\,\sigma }[s]]_{s+1}$
will have an even size. Let k be equal to
$[l_{l,\,\sigma }[s],\,r_{r,\,\sigma }[s]]_{s+1}$
will have an even size. Let k be equal to
![]() $|[l_{l,\,\sigma }[s],\,r_{r,\,\sigma }[s]]_{s+1}|$
.
$|[l_{l,\,\sigma }[s],\,r_{r,\,\sigma }[s]]_{s+1}|$
.
Further, we increase all blocks to the right of
![]() $r_{r,\sigma }[s]$
such that blocks keep the increasing order of sizes. Let
$r_{r,\sigma }[s]$
such that blocks keep the increasing order of sizes. Let
![]() $B=\{u_1<_{\mathcal {L}}\cdots <_{\mathcal {L}}u_m\}$
be a block such that
$B=\{u_1<_{\mathcal {L}}\cdots <_{\mathcal {L}}u_m\}$
be a block such that
![]() $r_{r,\sigma }[s]<_{\mathcal {L}}u_1$
. We choose the least unused odd numbers
$r_{r,\sigma }[s]<_{\mathcal {L}}u_1$
. We choose the least unused odd numbers
![]() $v_1,\,\ldots ,\, v_k$
and add them into the block B immediately to the right of
$v_1,\,\ldots ,\, v_k$
and add them into the block B immediately to the right of
![]() $u_m$
. Namely, we define
$u_m$
. Namely, we define
![]() $u_m<_{\mathcal {L}}v_1<_{\mathcal {L}}\cdots <_{\mathcal {L}} v_k$
and
$u_m<_{\mathcal {L}}v_1<_{\mathcal {L}}\cdots <_{\mathcal {L}} v_k$
and
![]() $S(u_m,\,v_{1})$
and
$S(u_m,\,v_{1})$
and
![]() $S(v_i,\,v_{i+1})$
for all
$S(v_i,\,v_{i+1})$
for all
![]() $i\in \{1,\,\ldots ,\,k-1\}$
. Since k is an even number, the number of B’s elements does not change the parity. We define
$i\in \{1,\,\ldots ,\,k-1\}$
. Since k is an even number, the number of B’s elements does not change the parity. We define
![]() $P(l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s], \sigma ,\,s+1)=0$
and, for all pairs
$P(l_{r,\,\sigma }[s],\,r_{l,\,\sigma }[s], \sigma ,\,s+1)=0$
and, for all pairs
![]() $u,\,v\in \mathcal {L}_{s+1}$
such that the successor relation is not defined yet, define
$u,\,v\in \mathcal {L}_{s+1}$
such that the successor relation is not defined yet, define
![]() $\neg S(u,\,v)$
. The outcome is
$\neg S(u,\,v)$
. The outcome is
![]() $\mathbf {1}$
.
$\mathbf {1}$
.
Case 2.4. Assume that
![]() $\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)\neq x_\sigma [s].$
We initialize all strategies
$\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)\neq x_\sigma [s].$
We initialize all strategies
![]() $R_\tau $
such that
$R_\tau $
such that
![]() $\tau =\sigma 1\mu $
(
$\tau =\sigma 1\mu $
(
![]() $\mu $
is an arbitrary binary string), and take off all protections
$\mu $
is an arbitrary binary string), and take off all protections
![]() $P(u,\,v,\,\tau ,\,s+1)=0$
for all
$P(u,\,v,\,\tau ,\,s+1)=0$
for all
![]() $u,\,v$
. Moreover, we take off protections defined by
$u,\,v$
. Moreover, we take off protections defined by
![]() $R_\sigma $
, and set
$R_\sigma $
, and set
![]() $y_{\sigma }[s+1]$
and
$y_{\sigma }[s+1]$
and
![]() $d_{\sigma }[s+1]$
to be undefined. The outcome is
$d_{\sigma }[s+1]$
to be undefined. The outcome is
![]() $\mathbf {0}$
.
$\mathbf {0}$
.
In all cases, if we not explicitly stated otherwise then we keep values of parameters without changes.
Case 3. The witness
![]() $y_\sigma [s]$
is defined and
$y_\sigma [s]$
is defined and
![]() $x_\sigma [s]$
is undefined. This case is possible, if the pre-image of
$x_\sigma [s]$
is undefined. This case is possible, if the pre-image of
![]() $y_\sigma [s]$
has changed. Then we try to find an appropriate
$y_\sigma [s]$
has changed. Then we try to find an appropriate
![]() $x_\sigma [s+1]$
by the following way.
$x_\sigma [s+1]$
by the following way.
As in Case
![]() $1$
, we check the existence of two blocks
$1$
, we check the existence of two blocks
![]() $B_{l}$
and
$B_{l}$
and
![]() $B_r$
satisfying conditions 3.1–3.5, where 3.1–3.3 are the same as 1.1–1.3, and instead of 1.4 we have the following:
$B_r$
satisfying conditions 3.1–3.5, where 3.1–3.3 are the same as 1.1–1.3, and instead of 1.4 we have the following:
3.4
![]() $\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)\in B_r$
.
$\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)\in B_r$
.
Additionally, we check the condition:
3.5 If
![]() $\sigma (i)=0$
then
$\sigma (i)=0$
then
![]() $\max (2^{w_\sigma [s]\cdot |\sigma |},2^6)<d_{\sigma \upharpoonright i}[s]$
for all
$\max (2^{w_\sigma [s]\cdot |\sigma |},2^6)<d_{\sigma \upharpoonright i}[s]$
for all
![]() $i<|\sigma |$
.
$i<|\sigma |$
.
If such blocks exist then we define
![]() $x_\sigma [s+1]=\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)$
, and
$x_\sigma [s+1]=\varphi ^{-1}_e(y_{\sigma }[s],\,s+1)$
, and
![]() $w_\sigma [s+1]=w_\sigma [s]+1$
. The other parameters are defined as in Case
$w_\sigma [s+1]=w_\sigma [s]+1$
. The other parameters are defined as in Case
![]() $1$
. Otherwise, we do nothing. In both the cases, the outcome is
$1$
. Otherwise, we do nothing. In both the cases, the outcome is
![]() $\mathbf {1}$
.
$\mathbf {1}$
.
This completes the description of the strategy
![]() $R_{\sigma }$
.
$R_{\sigma }$
.
3.4 The general strategy
Stage
![]() $0$
. Do stage
$0$
. Do stage
![]() $0$
of the strategy
$0$
of the strategy
![]() $R_\varepsilon $
and do stage
$R_\varepsilon $
and do stage
![]() $0$
of the strategy
$0$
of the strategy
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Stage
![]() $s+1$
. This stage has
$s+1$
. This stage has
![]() $s+2$
substages.
$s+2$
substages.
Substage
![]() $j=0$
. Do stage
$j=0$
. Do stage
![]() $s+1$
of the strategy
$s+1$
of the strategy
![]() $R_\varepsilon $
.
$R_\varepsilon $
.
Substage
![]() $j+1<s+1$
. Assume that the strategy
$j+1<s+1$
. Assume that the strategy
![]() $R_\tau $
has executed at substage j with outcome t. Then we do stage
$R_\tau $
has executed at substage j with outcome t. Then we do stage
![]() $s+1$
of the strategy
$s+1$
of the strategy
![]() $R_{\tau t}$
.
$R_{\tau t}$
.
Substage
![]() $s+1$
. Do stage
$s+1$
. Do stage
![]() $0$
of the strategies
$0$
of the strategies
![]() $R_\sigma $
for all
$R_\sigma $
for all
![]() $\sigma $
such that
$\sigma $
such that
![]() $|\sigma |=s+1$
. Do stage
$|\sigma |=s+1$
. Do stage
![]() $s+1$
of the strategy
$s+1$
of the strategy
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
4 The formal verification
In this section, we verify that all requirements
![]() $P_e$
are satisfied.
$P_e$
are satisfied.
Let now
![]() $\sigma $
be the leftmost path of the strategy tree which is working infinitely often.
$\sigma $
be the leftmost path of the strategy tree which is working infinitely often.
Lemma 4.1. The set of non-singleton blocks is co-final in
![]() $\mathcal {L}$
and has the order type
$\mathcal {L}$
and has the order type
![]() $\omega $
.
$\omega $
.
Proof Since at every stage
![]() $s+1$
an even number is added into
$s+1$
an even number is added into
![]() $\mathcal {L}_{s+1}$
as the greatest element, the set of even numbers is co-final in
$\mathcal {L}_{s+1}$
as the greatest element, the set of even numbers is co-final in
![]() $\mathcal {L}$
and has the order type
$\mathcal {L}$
and has the order type
![]() $\omega $
. Consequently, the set of blocks with even numbers is co-final in
$\omega $
. Consequently, the set of blocks with even numbers is co-final in
![]() $\mathcal {L}$
and has the order type
$\mathcal {L}$
and has the order type
![]() $\omega $
, also. We add a block with no even numbers between blocks with even numbers only. Therefore, the set of all blocks is co-final in
$\omega $
, also. We add a block with no even numbers between blocks with even numbers only. Therefore, the set of all blocks is co-final in
![]() $\mathcal {L}$
and has the order type
$\mathcal {L}$
and has the order type
![]() $\omega $
.
$\omega $
.
Lemma 4.2. For every i, the strategy
![]() $R_{\sigma \upharpoonright i}$
initialized finitely many times by the higher priority strategies.
$R_{\sigma \upharpoonright i}$
initialized finitely many times by the higher priority strategies.
Proof We use the induction by i. If
![]() $i=0$
then there is no strategy with higher priority than
$i=0$
then there is no strategy with higher priority than
![]() $R_{\varepsilon }$
and the statement of this lemma is trivial. Suppose that the lemma is proved for i. We prove it for
$R_{\varepsilon }$
and the statement of this lemma is trivial. Suppose that the lemma is proved for i. We prove it for
![]() $i+1$
. Assume that
$i+1$
. Assume that
![]() $s_0$
is the stage such that the strategy
$s_0$
is the stage such that the strategy
![]() $R_{\sigma \upharpoonright i}$
is not initialized by the strategies of higher priority after
$R_{\sigma \upharpoonright i}$
is not initialized by the strategies of higher priority after
![]() $s_0$
. Then after stage
$s_0$
. Then after stage
![]() $s_0$
the strategy
$s_0$
the strategy
![]() $R_{\sigma \upharpoonright i+1}$
can be initialized only by the strategy
$R_{\sigma \upharpoonright i+1}$
can be initialized only by the strategy
![]() $R_{\sigma \upharpoonright i}$
. Two cases are possible. If
$R_{\sigma \upharpoonright i}$
. Two cases are possible. If
![]() $\sigma (i)=0$
, then
$\sigma (i)=0$
, then
![]() $R_{\sigma \upharpoonright i+1}$
is not initialized by the strategies
$R_{\sigma \upharpoonright i+1}$
is not initialized by the strategies
![]() $R_{\sigma \upharpoonright i}$
. If
$R_{\sigma \upharpoonright i}$
. If
![]() $\sigma (i)=1$
then we can find stage
$\sigma (i)=1$
then we can find stage
![]() $s_1\geq s_0$
such that after this stage
$s_1\geq s_0$
such that after this stage
![]() $R_{\sigma \upharpoonright i}$
has outcome only
$R_{\sigma \upharpoonright i}$
has outcome only
![]() $\mathbf {1}$
and, consequently, this strategy does not initialize the strategy
$\mathbf {1}$
and, consequently, this strategy does not initialize the strategy
![]() $R_{\sigma \upharpoonright i+1}$
. Then after stage
$R_{\sigma \upharpoonright i+1}$
. Then after stage
![]() $s_1$
the strategy
$s_1$
the strategy
![]() $R_{\sigma \upharpoonright i+1}$
is not initialized by the strategies with higher priority.
$R_{\sigma \upharpoonright i+1}$
is not initialized by the strategies with higher priority.
Lemma 4.3. If
![]() $\sigma (i)=1$
then all parameters of
$\sigma (i)=1$
then all parameters of
![]() $R_{\sigma \upharpoonright i}$
are stabilized, i.e., there is a stage after which values of parameters are not changed.
$R_{\sigma \upharpoonright i}$
are stabilized, i.e., there is a stage after which values of parameters are not changed.
Proof By Lemma 4.2, there is a stage after which the strategy
![]() $R_{\sigma \upharpoonright i}$
is not initialized by the strategies with higher priority. Since
$R_{\sigma \upharpoonright i}$
is not initialized by the strategies with higher priority. Since
![]() $\sigma (i)=1$
, there is a stage after which the outcome of
$\sigma (i)=1$
, there is a stage after which the outcome of
![]() $R_{\sigma \upharpoonright i}$
is equal to
$R_{\sigma \upharpoonright i}$
is equal to
![]() $\mathbf {1}$
. Let
$\mathbf {1}$
. Let
![]() $s_0$
be the greatest of these two stages.
$s_0$
be the greatest of these two stages.
Suppose that after stage
![]() $s_0$
we have only Case
$s_0$
we have only Case
![]() $1$
of the construction. In this case parameters of
$1$
of the construction. In this case parameters of
![]() $R_{\sigma \upharpoonright i}$
are not defined at every stage and the statement is proved.
$R_{\sigma \upharpoonright i}$
are not defined at every stage and the statement is proved.
Now, we assume that there is a stage
![]() $s_1\geq s_0$
such that we have a case different from Case
$s_1\geq s_0$
such that we have a case different from Case
![]() $1$
at stage
$1$
at stage
![]() $s_1$
. Since we can return into Case
$s_1$
. Since we can return into Case
![]() $1$
only by the higher priority strategy initialization, after stage
$1$
only by the higher priority strategy initialization, after stage
![]() $s_1$
we do not have Case
$s_1$
we do not have Case
![]() $1$
.
$1$
.
Initially, we suppose that after stage
![]() $s_1$
we have only Case
$s_1$
we have only Case
![]() $3$
. Then the parameter
$3$
. Then the parameter
![]() $y_{\sigma \upharpoonright i}$
is defined and will be not changed, since the change is possible only by the higher priority strategy initialization. Other parameters are undefined and will be never defined. Consequently, the statement of the lemma has been proved.
$y_{\sigma \upharpoonright i}$
is defined and will be not changed, since the change is possible only by the higher priority strategy initialization. Other parameters are undefined and will be never defined. Consequently, the statement of the lemma has been proved.
Otherwise, suppose that there is a stage
![]() $s_2\geq s_1$
such that a case different from Case
$s_2\geq s_1$
such that a case different from Case
![]() $3$
(and Case
$3$
(and Case
![]() $1$
) holds at stage
$1$
) holds at stage
![]() $s_2$
. Note that Case 2.4 is not possible, since it has outcome
$s_2$
. Note that Case 2.4 is not possible, since it has outcome
![]() $\mathbf {0}$
. Consequently, we have one of Cases 2.1–2.3. After that we cannot return into Case
$\mathbf {0}$
. Consequently, we have one of Cases 2.1–2.3. After that we cannot return into Case
![]() $3$
. The returning can happen only in two cases: either the strategy
$3$
. The returning can happen only in two cases: either the strategy
![]() $R_{\sigma \upharpoonright i}$
does not change the parameter
$R_{\sigma \upharpoonright i}$
does not change the parameter
![]() $y_{\sigma \upharpoonright i}$
but can make it to be undefined in Case 2.4, or the parameter can be initialized by the higher priority strategy. Both cases are not possible by choosing stage
$y_{\sigma \upharpoonright i}$
but can make it to be undefined in Case 2.4, or the parameter can be initialized by the higher priority strategy. Both cases are not possible by choosing stage
![]() $s_0$
.
$s_0$
.
Thus, we have Cases 2.1–2.3 after stage
![]() $s_2$
. These cases do not change the parameters and, hence, the lemma is proved.
$s_2$
. These cases do not change the parameters and, hence, the lemma is proved.
Lemma 4.4. If
![]() $\sigma (i)=0$
then
$\sigma (i)=0$
then
![]() $y_{\sigma \upharpoonright i}$
is stabilizing.
$y_{\sigma \upharpoonright i}$
is stabilizing.
Proof By Lemma 4.2, there is a stage
![]() $s_0$
after which the strategy
$s_0$
after which the strategy
![]() $R_{\sigma \upharpoonright i}$
is not initialized by the higher priority strategy. By the lemma assumed, there is a stage
$R_{\sigma \upharpoonright i}$
is not initialized by the higher priority strategy. By the lemma assumed, there is a stage
![]() $s_1>s_0$
such that the outcome of the strategy is
$s_1>s_0$
such that the outcome of the strategy is
![]() $\mathbf {0}$
at stage
$\mathbf {0}$
at stage
![]() $s_1+1$
. It is possible only in Case 2.4, and, consequently, after executing stage
$s_1+1$
. It is possible only in Case 2.4, and, consequently, after executing stage
![]() $s_1$
the parameter
$s_1$
the parameter
![]() $y_{\sigma \upharpoonright i}$
was defined. By the construction, the strategy
$y_{\sigma \upharpoonright i}$
was defined. By the construction, the strategy
![]() $R_{\sigma \upharpoonright i}$
does not change the parameter
$R_{\sigma \upharpoonright i}$
does not change the parameter
![]() $y_{\sigma \upharpoonright i}$
. Only the higher priority strategy initialization can be the cause of the parameter change. By choosing
$y_{\sigma \upharpoonright i}$
. Only the higher priority strategy initialization can be the cause of the parameter change. By choosing
![]() $s_1$
, the parameter
$s_1$
, the parameter
![]() $y_{\sigma \upharpoonright i}$
will not be changed more.
$y_{\sigma \upharpoonright i}$
will not be changed more.
The next lemma plays a key role in the theorem’s proof.
Lemma 4.5. If
![]() $\sigma (i)=0$
then
$\sigma (i)=0$
then
![]() $\liminf \limits _{s\to \infty } d_{\sigma \upharpoonright i}[s]=\infty $
.
$\liminf \limits _{s\to \infty } d_{\sigma \upharpoonright i}[s]=\infty $
.
Proof By Lemmas 4.3 and 4.4, there exists a stage
![]() $s_0$
after which
$s_0$
after which
![]() $y_{\sigma \upharpoonright i}$
and all parameters of the strategies
$y_{\sigma \upharpoonright i}$
and all parameters of the strategies
![]() $R_{\sigma \upharpoonright j}$
with
$R_{\sigma \upharpoonright j}$
with
![]() $j<i$
and
$j<i$
and
![]() $\sigma (j)=1$
are stabilized.
$\sigma (j)=1$
are stabilized.
Initially, we consider the isolated situation when only the strategy
![]() $R_{\sigma \upharpoonright i}$
can change the constructing linear order. Then there are stages
$R_{\sigma \upharpoonright i}$
can change the constructing linear order. Then there are stages
![]() $s">s'>s_0$
at which
$s">s'>s_0$
at which
![]() $R_{\sigma \upharpoonright i}$
has outcome
$R_{\sigma \upharpoonright i}$
has outcome
![]() $\mathbf {0}$
, i.e., Case 2.4. holds. It means that the parameter
$\mathbf {0}$
, i.e., Case 2.4. holds. It means that the parameter
![]() $x_{\sigma \upharpoonright i}$
is defined before executing stage
$x_{\sigma \upharpoonright i}$
is defined before executing stage
![]() $s"$
, and the parameter
$s"$
, and the parameter
![]() $x_{\sigma \upharpoonright i}[s']$
is undefined. Consequently, there is a stage
$x_{\sigma \upharpoonright i}[s']$
is undefined. Consequently, there is a stage
![]() $s_1$
such that
$s_1$
such that
![]() $s">s_1>s'$
and
$s">s_1>s'$
and
![]() $x_{\sigma \upharpoonright i}[s_1]$
is defined. It can happen under execution of Cases 1 and 3. But by choosing of stage
$x_{\sigma \upharpoonright i}[s_1]$
is defined. It can happen under execution of Cases 1 and 3. But by choosing of stage
![]() $s_0$
, the strategy was not initialized by the higher priority strategies, and, consequently, Case
$s_0$
, the strategy was not initialized by the higher priority strategies, and, consequently, Case
![]() $3$
holds.
$3$
holds.
Let k be a number of pairs of successors located to the left of
![]() $x_{\sigma \upharpoonright i}[s_1]$
at stage
$x_{\sigma \upharpoonright i}[s_1]$
at stage
![]() $s_1$
. By conditions 3.1–3.4, there are k pairs of successors to the left of
$s_1$
. By conditions 3.1–3.4, there are k pairs of successors to the left of
![]() $y_{\sigma \upharpoonright i}[s_1]$
. Since Case 2.4 holds at stage
$y_{\sigma \upharpoonright i}[s_1]$
. Since Case 2.4 holds at stage
![]() $s"$
,
$s"$
,
![]() $\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")\neq x_{\sigma \upharpoonright i}[s_1]$
at this stage. Note that
$\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")\neq x_{\sigma \upharpoonright i}[s_1]$
at this stage. Note that
![]() $\varphi _i$
is correctly defined at all blocks to the left of
$\varphi _i$
is correctly defined at all blocks to the left of
![]() $\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")$
and the blocks of the linear order
$\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")$
and the blocks of the linear order
![]() $\mathcal {L}_{s_1}$
to the left of
$\mathcal {L}_{s_1}$
to the left of
![]() $x_{\sigma \upharpoonright i}[s_1]$
are coincide with the blocks of the linear order
$x_{\sigma \upharpoonright i}[s_1]$
are coincide with the blocks of the linear order
![]() $\mathcal {L}_{s"}$
to the left of
$\mathcal {L}_{s"}$
to the left of
![]() $x_{\sigma \upharpoonright i}[s"]=x_{\sigma \upharpoonright i}[s_1]$
(under assuming that other strategies do not change non-singleton blocks of the linear order).
$x_{\sigma \upharpoonright i}[s"]=x_{\sigma \upharpoonright i}[s_1]$
(under assuming that other strategies do not change non-singleton blocks of the linear order).
Since blocks of
![]() $W_e$
can expand only,
$W_e$
can expand only,
![]() $\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")$
and
$\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")$
and
![]() $x_{\sigma \upharpoonright i}[s_1]$
cannot be in the same block. Moreover,
$x_{\sigma \upharpoonright i}[s_1]$
cannot be in the same block. Moreover,
![]() $x_{\sigma \upharpoonright i}[s_1]<_{\mathcal {L}}\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")$
. Then the number of the successor pairs of
$x_{\sigma \upharpoonright i}[s_1]<_{\mathcal {L}}\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s")$
. Then the number of the successor pairs of
![]() $W_i$
to the left of
$W_i$
to the left of
![]() $y_{\sigma \upharpoonright i}[s_1]$
is strictly more than k. Thus, there is no stage
$y_{\sigma \upharpoonright i}[s_1]$
is strictly more than k. Thus, there is no stage
![]() $s"'$
such that
$s"'$
such that
![]() $\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s"')=x_{\sigma \upharpoonright i}[s_1]$
. Indeed,
$\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s"')=x_{\sigma \upharpoonright i}[s_1]$
. Indeed,
![]() $\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s"')$
and
$\varphi ^{-1}_i(y_{\sigma \upharpoonright i}[s_1], s"')$
and
![]() $x_{\sigma \upharpoonright i}[s_1]$
cannot be in the same block under the considered assuming.
$x_{\sigma \upharpoonright i}[s_1]$
cannot be in the same block under the considered assuming.
Now we use the arguments above to prove the lemma in the general case. By condition 3.5 of Case
![]() $3$
, there is a stage
$3$
, there is a stage
![]() $s_1>s_0$
such that
$s_1>s_0$
such that
![]() $d_{\sigma \upharpoonright i}[s_1]>2^n$
(
$d_{\sigma \upharpoonright i}[s_1]>2^n$
(
![]() $n\geq 6$
).
$n\geq 6$
).
Now we wish to argue that there is a stage
![]() $s_2>s_1$
such that
$s_2>s_1$
such that
![]() $d_{\sigma \upharpoonright i}[s_2]>2^{n+1}$
. By condition 3.5, if
$d_{\sigma \upharpoonright i}[s_2]>2^{n+1}$
. By condition 3.5, if
![]() $d_{\sigma \upharpoonright i}[s]< 2^{n+1}$
, then strategies
$d_{\sigma \upharpoonright i}[s]< 2^{n+1}$
, then strategies
![]() $R_{\sigma \upharpoonright j}$
can work to the left of
$R_{\sigma \upharpoonright j}$
can work to the left of
![]() $x_{\sigma \upharpoonright i}[s]$
only with
$x_{\sigma \upharpoonright i}[s]$
only with
![]() $j<n$
, and every such strategy can act at most n times. Thus, all such strategies can make at most
$j<n$
, and every such strategy can act at most n times. Thus, all such strategies can make at most
![]() $n^2$
changes of the linear order to the left of
$n^2$
changes of the linear order to the left of
![]() $x_{\sigma \upharpoonright i}[s]$
. After that, all strategies different from
$x_{\sigma \upharpoonright i}[s]$
. After that, all strategies different from
![]() $R_{\sigma \upharpoonright i}$
cannot make changes of the linear order before stage
$R_{\sigma \upharpoonright i}$
cannot make changes of the linear order before stage
![]() $s_2$
such that
$s_2$
such that
![]() $d_{\sigma \upharpoonright i}[s_2]>2^{n+1}$
. Due to arguments of the isolated situation, such a stage
$d_{\sigma \upharpoonright i}[s_2]>2^{n+1}$
. Due to arguments of the isolated situation, such a stage
![]() $s_2$
exists.
$s_2$
exists.
We will prove that at every stage
![]() $s'>s_2$
the following holds
$s'>s_2$
the following holds
![]() $d_{\sigma \upharpoonright i}[s']>2^{n}$
. Indeed, if it is not true, i.e., there is a stage
$d_{\sigma \upharpoonright i}[s']>2^{n}$
. Indeed, if it is not true, i.e., there is a stage
![]() $s'>s_2$
such that
$s'>s_2$
such that
![]() $d_{\sigma \upharpoonright i}[s']\leq 2^{n+1}$
then the construction can add at most
$d_{\sigma \upharpoonright i}[s']\leq 2^{n+1}$
then the construction can add at most
![]() $(n+1)^2$
new blocks to the left of
$(n+1)^2$
new blocks to the left of
![]() $x_{\sigma \upharpoonright i}[s_2]$
, and consequently,
$x_{\sigma \upharpoonright i}[s_2]$
, and consequently,
![]() $d_{\sigma \upharpoonright i}$
can decreased at most by
$d_{\sigma \upharpoonright i}$
can decreased at most by
![]() $(n+1)^2$
. Since
$(n+1)^2$
. Since
![]() $n\geq 6$
, we have
$n\geq 6$
, we have
![]() $d_{\sigma \upharpoonright i}[s']>d_{\sigma \upharpoonright i}[s_2]-(n+1)^2>2^{n+1}-(n+1)^2>2^n$
.
$d_{\sigma \upharpoonright i}[s']>d_{\sigma \upharpoonright i}[s_2]-(n+1)^2>2^{n+1}-(n+1)^2>2^n$
.
From the arguments above, it follows that
![]() $\liminf _s d_{\sigma \upharpoonright i}[s]=\infty $
.
$\liminf _s d_{\sigma \upharpoonright i}[s]=\infty $
.
Lemma 4.6. The linear order
![]() $\mathcal {L}$
is a strongly
$\mathcal {L}$
is a strongly
![]() $\eta $
-representation of a set.
$\eta $
-representation of a set.
Proof At every stage s, non-singleton blocks are located in the increasing order of sizes. During the construction, the sizes of blocks can only increase. By Lemma 4.1, it is enough to show that all blocks of
![]() $\mathcal {L}$
are finite. By the construction, only finitely many strategies work on the initial segment to the left of the block with element
$\mathcal {L}$
are finite. By the construction, only finitely many strategies work on the initial segment to the left of the block with element
![]() $2e$
. By the previous lemma, every such strategy can make finitely many actions on this initial segment: it can add new blocks or amalgamate two different blocks into one. Consequently, the sizes of blocks of this initial segment will not be increasing after all these strategies finished the action. Since the set of blocks with even numbers are co-final, the size of every block
$2e$
. By the previous lemma, every such strategy can make finitely many actions on this initial segment: it can add new blocks or amalgamate two different blocks into one. Consequently, the sizes of blocks of this initial segment will not be increasing after all these strategies finished the action. Since the set of blocks with even numbers are co-final, the size of every block
![]() $\mathcal {L}$
will be finite.
$\mathcal {L}$
will be finite.
The next lemma is finishing the proof.
Lemma 4.7. The strategy
![]() $R_{\sigma \upharpoonright e}$
satisfies the requirement
$R_{\sigma \upharpoonright e}$
satisfies the requirement
![]() $P_e$
.
$P_e$
.
Proof Suppose that
![]() $\varphi ^{\emptyset "}_e$
is an isomorphism of linear orders
$\varphi ^{\emptyset "}_e$
is an isomorphism of linear orders
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $W_e$
and
$W_e$
and
![]() $\varphi ^{\emptyset '}_e(\cdot ,\,s)$
is an approximation of this isomorphism. Recall that we use
$\varphi ^{\emptyset '}_e(\cdot ,\,s)$
is an approximation of this isomorphism. Recall that we use
![]() $\varphi _e(\cdot ,\,s)$
instead of
$\varphi _e(\cdot ,\,s)$
instead of
![]() $\varphi ^{\emptyset '}_e(\cdot ,\,s)$
to shorten the notation.
$\varphi ^{\emptyset '}_e(\cdot ,\,s)$
to shorten the notation.
If
![]() $\sigma (e)=0$
then, by Lemma 4.3, the value
$\sigma (e)=0$
then, by Lemma 4.3, the value
![]() $y_{\sigma \upharpoonright e}$
is stabilized after an appropriate stage and, by Lemma 4.5,
$y_{\sigma \upharpoonright e}$
is stabilized after an appropriate stage and, by Lemma 4.5,
![]() $(\forall u\in \mathcal {L})\,(\exists s_0)\,(\forall s>s_0)\, [\varphi ^{-1}_e(y_{\sigma \upharpoonright e},\,s)>_{\mathcal {L}}u]$
, i.e.,
$(\forall u\in \mathcal {L})\,(\exists s_0)\,(\forall s>s_0)\, [\varphi ^{-1}_e(y_{\sigma \upharpoonright e},\,s)>_{\mathcal {L}}u]$
, i.e.,
![]() $y_{\sigma \upharpoonright e}$
does not have a pre-image in the limit. It is a contradiction with the supposing that
$y_{\sigma \upharpoonright e}$
does not have a pre-image in the limit. It is a contradiction with the supposing that
![]() $\varphi ^{\emptyset "}_e(\cdot ,\,s)$
is an isomorphism.
$\varphi ^{\emptyset "}_e(\cdot ,\,s)$
is an isomorphism.
Now we assume that
![]() $\sigma (e)=1$
. Let
$\sigma (e)=1$
. Let
![]() $s_0$
be a stage after that the strategy
$s_0$
be a stage after that the strategy
![]() $R_{\sigma \upharpoonright e}$
is not initialized by the higher priority strategies and the outcome of this strategy and all strategies
$R_{\sigma \upharpoonright e}$
is not initialized by the higher priority strategies and the outcome of this strategy and all strategies
![]() $R_{\sigma \upharpoonright i}$
(
$R_{\sigma \upharpoonright i}$
(
![]() $i<e$
) with
$i<e$
) with
![]() $\sigma (i)=1$
is equal to
$\sigma (i)=1$
is equal to
![]() $1$
. Using the arguments of Lemma 4.3, we can show that there is a stage
$1$
. Using the arguments of Lemma 4.3, we can show that there is a stage
![]() $s_1>s_0$
such that one of the following three conditions holds.
$s_1>s_0$
such that one of the following three conditions holds.
(1) Suppose that Case
![]() $1$
of the strategy
$1$
of the strategy
![]() $R_{\sigma \upharpoonright e}$
holds at every stage after
$R_{\sigma \upharpoonright e}$
holds at every stage after
![]() $s_1$
. By choosing stage
$s_1$
. By choosing stage
![]() $s_0$
, all parameters of strategies
$s_0$
, all parameters of strategies
![]() $R_{\sigma \upharpoonright i}$
with
$R_{\sigma \upharpoonright i}$
with
![]() $i<e$
and
$i<e$
and
![]() $\sigma (i)=1$
are stabilized and we can consider non-singleton blocks
$\sigma (i)=1$
are stabilized and we can consider non-singleton blocks
![]() $B_{r,\,\sigma \upharpoonright i}$
. Note that there are finitely many such blocks and, by Lemma 4.1, there are adjacent non-singleton blocks
$B_{r,\,\sigma \upharpoonright i}$
. Note that there are finitely many such blocks and, by Lemma 4.1, there are adjacent non-singleton blocks
![]() $B_l<_{\mathcal {L}}B_r$
of
$B_l<_{\mathcal {L}}B_r$
of
![]() $\mathcal {L}$
which are located to the right of
$\mathcal {L}$
which are located to the right of
![]() $B_{r,\,\sigma \upharpoonright i}$
. Let
$B_{r,\,\sigma \upharpoonright i}$
. Let
![]() $s_2$
be a stage after which
$s_2$
be a stage after which
![]() $\varphi _e$
is not changed on
$\varphi _e$
is not changed on
![]() $B_r$
and on non-singleton blocks to the left of
$B_r$
and on non-singleton blocks to the left of
![]() $B_r$
(by Lemma 4.6, this set is finite and, consequently, the required stage exists). Then at every stage
$B_r$
(by Lemma 4.6, this set is finite and, consequently, the required stage exists). Then at every stage
![]() $s>s_2$
the conditions 1.1 and 1.2 of Case
$s>s_2$
the conditions 1.1 and 1.2 of Case
![]() $1$
hold. The condition
$1$
hold. The condition
![]() $B_{r,\,\sigma \upharpoonright i}<_{\mathcal {L}}B_l<_{\mathcal {L}}B_r$
(
$B_{r,\,\sigma \upharpoonright i}<_{\mathcal {L}}B_l<_{\mathcal {L}}B_r$
(
![]() $i<e$
and
$i<e$
and
![]() $\sigma (i)=1$
) of point 1.3 holds. It is remain to note that, by Lemma 4.5, there is a stage
$\sigma (i)=1$
) of point 1.3 holds. It is remain to note that, by Lemma 4.5, there is a stage
![]() $s_3>s_2$
such that for every
$s_3>s_2$
such that for every
![]() $s>s_3$
and
$s>s_3$
and
![]() $i<e$
with
$i<e$
with
![]() $\sigma (i)=0$
we have
$\sigma (i)=0$
we have
![]() $\varphi ^{-1}(y_{\sigma \upharpoonright i},\,s)>_{\mathcal {L}}B_r$
. It is a contradiction with
$\varphi ^{-1}(y_{\sigma \upharpoonright i},\,s)>_{\mathcal {L}}B_r$
. It is a contradiction with
![]() $B_{r,\,\sigma \upharpoonright i}<_{\mathcal {L}}B_l<_{\mathcal {L}}B_r$
and
$B_{r,\,\sigma \upharpoonright i}<_{\mathcal {L}}B_l<_{\mathcal {L}}B_r$
and
![]() $\varphi ^{-1}(y_{\sigma \upharpoonright i},\,s)\in B_{r,\,\sigma \upharpoonright i}$
. Consequently, the function
$\varphi ^{-1}(y_{\sigma \upharpoonright i},\,s)\in B_{r,\,\sigma \upharpoonright i}$
. Consequently, the function
![]() $\varphi _e(\cdot ,\,s)$
cannot be an approximation of an isomorphism.
$\varphi _e(\cdot ,\,s)$
cannot be an approximation of an isomorphism.
(2) Suppose that Case
![]() $3$
always holds after stage
$3$
always holds after stage
![]() $s_1$
. It is not hard to see, if
$s_1$
. It is not hard to see, if
![]() $\varphi _e(\cdot ,\,s)$
is an approximation of an isomorphism then there is a stage
$\varphi _e(\cdot ,\,s)$
is an approximation of an isomorphism then there is a stage
![]() $s_2>s_1$
such that all conditions 3.1–3.4 are true. By Lemma 4.5, we have
$s_2>s_1$
such that all conditions 3.1–3.4 are true. By Lemma 4.5, we have
![]() $\liminf _s d_{\sigma \upharpoonright i}[s]=\infty $
for every
$\liminf _s d_{\sigma \upharpoonright i}[s]=\infty $
for every
![]() $i<e$
such that
$i<e$
such that
![]() $\sigma (i)=0$
. Consequently, there is a stage
$\sigma (i)=0$
. Consequently, there is a stage
![]() $s_3>s_2$
such that
$s_3>s_2$
such that
![]() $2^{w_\sigma [s_2]\cdot |\sigma |}<d_{\sigma \upharpoonright i}[s_3]$
. If
$2^{w_\sigma [s_2]\cdot |\sigma |}<d_{\sigma \upharpoonright i}[s_3]$
. If
![]() $s_3$
is the least stage with the condition above then
$s_3$
is the least stage with the condition above then
![]() $w_{\sigma }[s_2] = w_{\sigma }[s]$
for every
$w_{\sigma }[s_2] = w_{\sigma }[s]$
for every
![]() $s\in \{s_2,s_2+1,\ldots ,s_3\}$
. Then condition 3.5 is true and the parameter
$s\in \{s_2,s_2+1,\ldots ,s_3\}$
. Then condition 3.5 is true and the parameter
![]() $x_\sigma $
is defined at this stage and, consequently, we have the case at stage
$x_\sigma $
is defined at this stage and, consequently, we have the case at stage
![]() $s_3+1$
which is different from Case
$s_3+1$
which is different from Case
![]() $3$
. It is a contradiction with supposing of this case. Consequently, the function
$3$
. It is a contradiction with supposing of this case. Consequently, the function
![]() $\varphi _e(\cdot ,\,s)$
is not an approximation of an isomorphism.
$\varphi _e(\cdot ,\,s)$
is not an approximation of an isomorphism.
(3) At every stage after stage
![]() $s_1$
we have Case
$s_1$
we have Case
![]() $2$
. Since
$2$
. Since
![]() $\sigma (i)=1$
, Case 2.4 never happens again. Then we have the following subcases.
$\sigma (i)=1$
, Case 2.4 never happens again. Then we have the following subcases.
Subcase A. Suppose that there are infinitely many stages such that Case 2.1 holds. Since the values of the parameters of the strategy
![]() $R_{\sigma \upharpoonright e}$
have no changes after stage
$R_{\sigma \upharpoonright e}$
have no changes after stage
![]() $s_1$
,
$s_1$
,
![]() $B_{r,\,\sigma \upharpoonright e}$
has no changes too. If
$B_{r,\,\sigma \upharpoonright e}$
has no changes too. If
![]() $\varphi _e$
is an approximation of an isomorphism then there must exist a stage
$\varphi _e$
is an approximation of an isomorphism then there must exist a stage
![]() $s_2>s_1$
such that
$s_2>s_1$
such that
![]() $\varphi _e$
is the same as an isomorphism at blocks to the left of
$\varphi _e$
is the same as an isomorphism at blocks to the left of
![]() $B_{r,\,\sigma \upharpoonright e}$
at every stage after stage
$B_{r,\,\sigma \upharpoonright e}$
at every stage after stage
![]() $s_2$
. Then Case 2.1 cannot happen after stage
$s_2$
. Then Case 2.1 cannot happen after stage
![]() $s_2$
. It is a contradiction with the supposing.
$s_2$
. It is a contradiction with the supposing.
Subcase B. Suppose that Case 2.2 holds after some stage
![]() $s_2$
. We argue that it is not possible. Since the approximation looks correctly, the images of
$s_2$
. We argue that it is not possible. Since the approximation looks correctly, the images of
![]() $B_{l,\,{\sigma \upharpoonright e}}$
and
$B_{l,\,{\sigma \upharpoonright e}}$
and
![]() $B_{r,\,{\sigma \upharpoonright e}}$
belong to different blocks of the linear order
$B_{r,\,{\sigma \upharpoonright e}}$
belong to different blocks of the linear order
![]() $W_{e,\,s}$
at every stage
$W_{e,\,s}$
at every stage
![]() $s>s_2$
. Consequently, any preset number of elements must be enumerated between them, in particular
$s>s_2$
. Consequently, any preset number of elements must be enumerated between them, in particular
![]() $2|[l_{r,\,{\sigma \upharpoonright e}},\,r_{l,\,{\sigma \upharpoonright e}}]_s|$
. The Case 2.3 holds at the appropriate stage. We have a contradiction.
$2|[l_{r,\,{\sigma \upharpoonright e}},\,r_{l,\,{\sigma \upharpoonright e}}]_s|$
. The Case 2.3 holds at the appropriate stage. We have a contradiction.
Subcase C. There are infinitely many stages such that Case 2.3 holds. Suppose that Case 2.3 holds at a stage
![]() $s_3>s_2$
. Then at stage
$s_3>s_2$
. Then at stage
![]() $s_3+1$
either the approximation looks incorrectly and we have Case 2.1, or the approximation looks correctly and, consequently, the pre-image of
$s_3+1$
either the approximation looks incorrectly and we have Case 2.1, or the approximation looks correctly and, consequently, the pre-image of
![]() $y_{\sigma \upharpoonright e}$
is changed, i.e., we have Case 2.4. Again, we have a contradiction with choosing
$y_{\sigma \upharpoonright e}$
is changed, i.e., we have Case 2.4. Again, we have a contradiction with choosing
![]() $s_2>s_1$
.
$s_2>s_1$
.
Since we have contradictions at every subcase A, B, and C, the function
![]() $\varphi _e(\cdot ,\,s)$
is not an approximation of an isomorphism. Thus, the lemma is completely proved.
$\varphi _e(\cdot ,\,s)$
is not an approximation of an isomorphism. Thus, the lemma is completely proved.
![]() $\dashv $
$\dashv $
5. Acknowledgments
The authors are grateful to the anonymous reviewer for the great work to make Section 2 more clear. The work of the first author was supported by RFBR grant no. 20-31-70012. The work of the second author was supported by the Russian Science Foundation (project no. 18-11-00028) and performed under the development program of the Volga Region Mathematical Center (agreement no. 075-02-2020-1478).