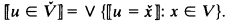Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1978.
Vol. 79,
Issue. ,
p.
596.
Magidor, Menachem
1979.
On the existence of nonregular ultrafilters and the cardinality of ultrapowers.
Transactions of the American Mathematical Society,
Vol. 249,
Issue. 1,
p.
97.
Taylor, Alan D.
1979.
Regularity properties of ideals and ultrafilters.
Annals of Mathematical Logic,
Vol. 16,
Issue. 1,
p.
33.
1980.
Set Theory An Introduction to Independence Proofs.
Vol. 102,
Issue. ,
p.
305.
Väänänen, Jouko
1980.
The Hanf number of 𝐿_{𝜔₁𝜔₁}.
Proceedings of the American Mathematical Society,
Vol. 79,
Issue. 2,
p.
294.
Tall, Franklin D.
1980.
Surveys in General Topology.
p.
445.
Magidor, Menachem
1980.
Precipitous ideals and Σ 1 4 setssets.
Israel Journal of Mathematics,
Vol. 35,
Issue. 1-2,
p.
109.
Balcar, Bohuslav
Simon, Petr
and
Vojtáš, Peter
1981.
Refinement properties and extensions of filters in Boolean algebras.
Transactions of the American Mathematical Society,
Vol. 267,
Issue. 1,
p.
265.
Todorčević, Stevo B.
1981.
Trees, subtrees and order types.
Annals of Mathematical Logic,
Vol. 20,
Issue. 3,
p.
233.
Antonovskij, Mikhail Y.
Chudnovsky, David V.
Chudnovsky, Gregory V.
and
Hewitt, Edwin
1981.
Rings of real-valued continuous functions. II.
Mathematische Zeitschrift,
Vol. 176,
Issue. 2,
p.
151.
Kanamori, A.
1982.
PATRAS LOGIC SYMPOSION.
Vol. 109,
Issue. ,
p.
339.
Laver, Richard
1982.
Logic Colloquium '80 - Papers intended for the European Summer Meeting of the Association for Symbolic Logic.
Vol. 108,
Issue. ,
p.
173.
Baumgartner, James E.
and
Taylor, Alan D.
1982.
Saturation properties of ideals in generic extensions. I.
Transactions of the American Mathematical Society,
Vol. 270,
Issue. 2,
p.
557.
Laver, Richard
1982.
PATRAS LOGIC SYMPOSION.
Vol. 109,
Issue. ,
p.
297.
Baumgartner, James E.
and
Taylor, Alan D.
1982.
Saturation properties of ideals in generic extensions. II.
Transactions of the American Mathematical Society,
Vol. 271,
Issue. 2,
p.
587.
Foreman, Matthew
1982.
Large cardinals and strong model theoretic transfer properties.
Transactions of the American Mathematical Society,
Vol. 272,
Issue. 2,
p.
427.
Foreman, Matthew
1983.
Cabal Seminar 79–81.
Vol. 1019,
Issue. ,
p.
1.
Donder, Hans-Dieter
and
Koepke, Peter
1983.
On the consistency strength of ‘Accessible’ Jonsson Cardinals and of the Weak Chang Conjecture.
Annals of Pure and Applied Logic,
Vol. 25,
Issue. 3,
p.
233.
Mitchell, William J.
1984.
The core model for sequences of measures. I.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 95,
Issue. 2,
p.
229.
Laver, Richard
1984.
Precipitousness in forcing extensions.
Israel Journal of Mathematics,
Vol. 48,
Issue. 2-3,
p.
97.
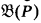 is the associated cBa. We write VP for
is the associated cBa. We write VP for 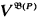 .
.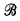 is κ-complete iff sups of subsets of
is κ-complete iff sups of subsets of 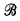 of cardinality less than κ always exist.
of cardinality less than κ always exist.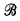 is a cBa, x̌ is the object in
is a cBa, x̌ is the object in 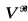 representing x in V. In many cases, especially with ordinals, the ̌ is dropped. V̌ is the Boolean-valued class representing V — i.e.,
representing x in V. In many cases, especially with ordinals, the ̌ is dropped. V̌ is the Boolean-valued class representing V — i.e.,