Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T07:44:06.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Cardinal functions on ultra products of Boolean algebras

Published online by Cambridge University Press:  12 March 2014

Douglas Peterson
Douglas Peterson*
Affiliation:
1434 Hover St. #5, Longmont, CO 80501, USA
Get access Rights & Permissions [Opens in a new window]

Extract

This article is concerned with functions k assigning a cardinal number to each infinite Boolean algebra (BA), and the behaviour of such functions under ultraproducts. For some common functions k we have

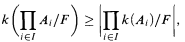
for others we have ≤ instead, under suitable assumptions. For the function π character we go into more detail. More specifically, ≥ holds when F is regular, for cellularity, length, irredundance, spread, and incomparability. ≤ holds for π. ≥ holds under GCH for F regular, for depth, π, πχ, χ, h-cof, tightness, hL, and hd. These results show that ≥ can consistently hold in ZFC since if V = L holds then all uniform ultrafilters are regular. For π-character we prove two more results: (1) If F is regular and ess 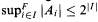, then

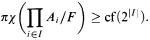
(2) It is relatively consistent to have 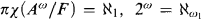, where A is the denumerable atomless BA.

A thorough analysis of what happens without the assumption that F is regular can be found in Rosłanowski, Shelah [8] and Magidor, Shelah [5]. Those papers also mention open problems concerning the above two possible inequalities.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 1 , March 1997 , pp. 43 - 59
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bell, M. and Kunen, K., On the PI character of ultrafilters, Comptes Rendus Mathématiques, vol. 3 (1981), pp. 351–356.Google Scholar
[2]Keisler, H. J. and Prikry, K., A result concerning cardinalities of ultraproducts, this Journal, vol. 39 (1974), no. 1, pp. 43–48.Google Scholar
[3]Koppelberg, S., Handbook of Boolean algebras, vol. 1, North-Holland, 1989.Google Scholar
[4]Kunen, K., Set theory, North-Holland, 1980.Google Scholar
[5]Magidor, M. and Shelah, S., On the length of ultraproducts of Boolean algebras, preprint, 1991.Google Scholar
[6]McKenzie, R. and Monk, J. D., Chains on Boolean algebras, Annals of Mathematical Logic, vol. 22 (1982), pp. 137–175.CrossRefGoogle Scholar
[7]Monk, J. D., Cardinal functions on Boolean algebras, Birkhäuser, 1990.CrossRefGoogle Scholar
[8]Rosłanowski, A. and Shelah, S., F-99: Notes on cardinal invariants and ultraproducts of Boolean algebras, preprint, 1994.Google Scholar