Introduction
The estimation of ice-sheet volume variations is one of the goals of satellite radar altimetry. However, the major obstacle to the correct interpretation of altimetric data lies in the complex and variable nature of the reflecting snowpack. Indeed, the penetration of radar waves into the snowpack depends on the characteristics of the medium that exhibit both spatial and temporal variability. The lack of knowledge of penetration depth then directly enters into the altimetric height-error budget. Microwave penetration within the snowpack has already been empirically (Reference Ridley and PartingtonRidley and Partington, 1988; Reference Davis and ZwallyDavis and Zwally, 1993) and theoretically (Reference Hofer and MätzlerHofer and Mätzler, 1980; Reference Ulaby, Moore and FungUlaby and others, 1986) estimated for a few specific cases. To our knowledge, this quantity has not been mapped at the continental scale. The same statement applies to the temporal variability of the microwave observations, which has already been pointed out by Ridley and Reference Ridley and BamberBamber (1995) and Reference Rots, Sturm and MillerRott and others (1993a, Reference Rott, Storm and Millerb).
The aims of this paper are to analyse temporal microwave variations at short time-scales and to map the penetration depth at global scales. The analysis is based on the study of short time-scale (≤1 month) variations of the radar-echo parameters (back-scattering, leading-edge width and trailing-edge slope of the altimetric wave form), taking advantage of the ERS1 data acquired during phase B. This ERS1 phase B was characterized by a 3 d orbit repeat cycle when the satellite operated in “ocean mode”. The corresponding distance between adjacent ground tracks was 380 km at 66° latitude and 145 km at 81° latitude. Despite the short duration (2 months) and poor coverage (large gaps between tracks), the orbit provides a good compromise between spatial and temporal-scale sampling using a single satellite. For Antarctic coverage, the spatial density of (lie measurement is good south of 75° S and deteriorates throughout the north of the continent.
Such an orbit allows US to assess correctly changes in radar altimetric signal events of duration between 6 days and 1 month with sizes of more than a few tens of kilometres along-track to more than a few hundred kilometres over the Antarctic continent.
The determination of accurate surface topography and geophysical characteristics of the snowpack from altimetric radar wave form is an underdetermined problem for two reasons. First, the topography (height and roughness) is not homogeneous at the radar footprint scale (which is not consistent with Reference BrownBrown’s (1977) assumption. This has been discussed by Reference Legrésy and RémyLegrésy and Rémy (1997). The presence of undulations at the footprint scale affects the whole altimetric wave form and makes the inversion of the wave-form data for other geophysical parameters difficult. The second problem is linked to the “volume effect” and has two aspects. The first aspect is the non-linearity of the superposition of volume signal to the deformation of the echo by the surface topography at small scales (e.g. 1-10 km). The second aspect is that the inversion depends on antenna and orbit characteristics which varies from one satellite mission to another.
A fully realistic wave-form model should of course take into account effects described previously, which would make the inversion problem very complex and certainly computationally prohibitive with respect to simpler conventional models. In any case, because the simultaneous estimation of topographic and snowpack characteristics from waveform inversion is cumbersome, a two-step method can be formulated. The first step would classically consist of cstimating the pertinent parameters describing the altimetric response. These are the back-scattering coefficient (σ0), the width of the leading edge (Tr) and the logarithmic slope of the trailing edge (Fl), following Reference Legrésy and RémyLegrésy and Rémy (1997). The second step would then consist of using the altimetric parameters to recover the geophysical characteristics of the snowpack. The main original aspect presented here is that our inversion uses the temporal variations of all the parameters to remove one degree of freedom from the initial “topography + snowpack characteristics” inversion problem.
In the first part of this paper, we shall establish the temporal variations of the radar echo. The observed temporal variations can be caused either by the non-reproducibility of the altimetric measurement or by temporal variability of the snowpack at the surface of ice sheets (Reference LegrésyLegrésy, 1995). These variations are due to meteorological phenomena affecting the surface micro-roughness. Changes in micro-roughness affect the ratio between surface and volume signal in the echo and also distort the altimetric wave form. Consequently, there is an artificial variability in the waveform descriptive parameters and in the height measurement. In the second part of this paper, we will take advantage of this variability to add more information to the problem of the altimetric signal inversion and we will then invert a wave-form model.
1. Temporal Variations of the Altimetric Signal: A One-Track Case Study
We have used data from the 22 3 d repeat cycles from the ERS1 phase B orbit configuration (January-February 1992). Each cycle contains 43 tracks (see Fig. 1). To derive temporal variability of altimetric parameters, the classical way is to build first a reference mean profile for each parameter and then to look at the anomalies with respect to the mean. This will now be described.

Fig. 1. Map of Antarctica. Contour interval is 100 m. The tracks of (he ERS1 3 d repeat cycle are marked as small dots and the 1050 km track used in this paper is plotted in bold.
The studied track (Fig. 1) is 1050 km long and includes 3000 individual repeal measurements. In fact, only 13 repeat tracks have been used, owing to gaps in the dataset and to erroneous data that have been removed.
1.1. Description of a mean track
Figure 2 presents the mean altimetric parameters (H. σ°, Tr and Fl averaged over the 13 repeat measurements) along the track. In the first half of the track (0-500 km), the back-scattering coefficient has low values, while the leading-edge width and the trailing-edge slope have high values. This is the signature of a volume echo (Reference Legrésy and RémyLegrésy and Rémy 1997). In the second half of the track, the presence of a volume echo is not marked. Indeed, the back-scattering coefficient is higher than in the first half of the profile, whereas the leading-edge width and the trailing-edge slope have lower values. Notice that this is a first-order approach that should be considered with caution, because of the high noise level on the leading-edge width and the trailing-edge slope parameters. The main difficulty in building the mean profiles is due to non-exact repeatability of the ground track, i.e. the ground-track band width is about ±1 km with respect to a reference (Reference RosengrenRosengren, 1992). In fact, at high latitudes, the shift between the two tracks reaches a maximum of 3/100° in longitude and 3/1000° in latitude.

Fig. 2. Mean profiles of the 1050 km track displayed in Figure 1. The height (a)ranges from 3000 to 3300 m. The back-scattering coefficient (b) varies by 4 dB, being lower at the beginning of the profile. The leading-edge width (c) ranges from 2 to 5 altimetric gates (e.g. 47 cm equivalent in height), being higher at the beginning of the profile. The trailing-edge slope (d) is highly variable and presents a large-scale decrease of 50 x 10 -4 Npgate -1 between the first and second half of the profile.
In this case, one may consider that wave-form parameters arc not affected by the geographical displacement if they are smoothed over more than 10 km. (Reference Legrésy and RémyLegrésy and Rémy, 1997). Another source of error in the mean profile interpretation is the slope error. In the case of a 0- 2.5%? slope rate (at the scale of the radar footprint) that is observed along the track, the induced error on individual height ranges from 0 to 2.5 m which is not acceptable. To correct for this error, we computed the across-track topography over a 2 km band applying a total inversion technique to the ERS1 geodetic cycles data as explained in Brisset and Rémy (1996): 743 tracks in the across direction of the 1000 km observed track were used, leading to a 1.4km average distance between each track to be processed through the inversion. The height measurement is then corrected for this displacement by subtracting the geodetic topography precisely interpolated at each point. Finally, the height measurement is also perturbed by orbit errors. The orbit-error spectrum shows dominant peaks at very long wavelengths (> several tens of thousands of kilometres) (Minster and others, 1992). This orbit error is therefore assumed as only a constant bias on the 1000 km tracks.
1.2. Temporal variations along a single track
The next step in the processing consists of computing the temporal anomalies of the altimetric parameters (Fig. 3) about their mean values. To reduce short-scale noise of the altimetric parameters, the data have been smoothed spatially along the track (using an average sliding window of 10 km width) and in time (using a 9day window) because of data gaps either due to lost altimeter tracks or to data editing.

Fig. 3. Temporal anomalies of the waveform parameters, (a) The back-scattering coefficient (in dB), (b) the leading-edge width (in gates), (c) the trailing-edge slope (in 10 -4 Np gate-1) about the mean shown in Figure 2.
One then finds that the radar back-scattering coefficient shows coherent variations by ± 1dB at about 15 d time-scales. At the same time, anti-correlated variations occur on the leading edge width (± 0.5 m or 1 gate).The trailing-edge slope does not present a very coherent signal. The significant variations occur particularly on the first half of the track, while the second half does not present the same level of sensitivity. Note that the height parameter, extracted from the wave-form leading edge is also affected. Figure 4 displays the temporal anomaly of the parameters averaged over the first 500 km of the track and illustrates the phenomenon. In this figure, the temporal variations averaged over the last 500km have been removed (region displaying very low variability). This allows the removal of the- orbit bias error on the height and reveals the difference of signal between the beginning and the end of the track.

Fig. 4. Average anomaly of the parameters over the first half of the track.
Figure 4 also shows that there are 70-80 cm height variations within a short period of time. While this signal is the average of 1400 individual measurements at each date, the confidence in the observed variations is at the 3 cm level in height. This is, of course, an unrealistic magnitude given the low accumulation in the region and the short time-scales involved. We will now investigate some reasons for this artifact. Several possible back-scattering variation mechanisms may be investigated. First, potential causes can lie in the topographic undulations across track (Legrésy and Rémy, 1997). However, the geodetic topography does not present undulations across-track with sufficient amplitudes to modify the back-scattering as observed. A second cause may arise from natural geographical variations in back-scattering in the across-track direction, other than those due to undulations, with amplitudes comparable to the observed 1 dB. Such a reflecting area (for example, a high reflecting but small area) is spread over ~10km scales on the altimetric back-scattering (Legrésy and Rémy, 1997) and is thus geometrically impossible here (50 dB in amplitude, a few metres wide and 500km long is not realistic). Also, neither mis-pointing nor σ° instrumental drift can be invoked because the ERS1 platform is stable at 0.01 ° and there is no σ° drift observed at ibis time-scale. The last potential cause may arise from the volume-echo contribution to the radar reflection. As already mentioned, the area that exhibits strong temporal variations is affected by volume echo. The observed variations (anti-correlation between σ° and Tr,Fl) suggest a variation of the surface signal. Indeed, a decrease of the surface back-scattering diminishes the total back-scattering and increases the relative weight of the volume part of the signal. As a consequence, the leading edge and the trailing edge are increased. On the other hand, an increase of the surface back-scattering will emphasize the surface characteristics of a wave form which will then display a narrower leading edge and a more sloping trailing edge.
Thus, it is clear that the identified artificial variations in height are highly correlated with variations in back-scattering (and anti-correlated with variations in leading-edge width).
This artifact is limited by “low-retracking” techniques (Bamber, 1994; Legrésy, 1995). These techniques consider the beginning of the leading edge (for example 25% of the total amplitude). In this case, the observed signal reduces to 50-60 cm in amplitude, because it is less sensitive to volume echo which acts principally at the end of the wave form. However, the artificial signal is still present at a significant level with respect to the height-accuracy requirements for glaciological measurements, and the interpretation of the measurement becomes biased. This means that any waveform retracking method, not including the volume-echo contribution, may create artificial height variations that should not be interpreted in geophysical terms.
2. Temporal Variations Over the Antarctic Continent
After the analysis of a 1000 km track case study, it is of interest to extend the study over the whole continent. Even if the spatial coverage is sparse (Fig. 1), it is sufficient to continue a conclusive prospective work. To this end, we computed the data from 22 repeat cycles over the whole continent.
2.1. rms variability
Mean values of each parameter were computed over a 2° longitude by 0.5° latitude grid and mean values arc effectively computed in locations where at least 50 data and 11 repeat measurements are available in order to perform significant statistical analyses. Each track is computed independently in order to minimize poor geographical repeatability of the measurements (in the case of multiple tracks within a grid element), and to avoid problems of repeatability between ascending and descending observations (Brisset, 1996). Figure 5 shows maps of the temporal variability in the various parameters in terms of rms. The variability may reach 0.5 m for the leading edge width, 1 dB for the back-scattering and 25 units for the trailing-edge slope. The possible variability caused by thermal noise, speckle and retracting is less than 10% of what is observed here. This variability leads to a “potential variability” of 0.5 m rms in the height measurement at 2 months scale. Unlike the retracking error, thermal or speckle noise that are random has spatial correlation over a few hundred kilometres. This error made on the height measurement therefore seems to dominate over other known sources and occurs all over the continent. It is hence necessary to understand well the origin and character of this error.

Fig. 5. Maps of the rms variability of the various parameters over the Antarctic ice sheet. (a) The back-scattering coefficient (in dB), (b) the leading-edge width (in gates), (c) the trailing-edge slope (in 10-4 Np gate-1).
2.2. Physical processes of variation
Variations in the volume part of the signal due to variations in the snowpack temperature, for instance, or to variations in absorption, would not act similarly (an increase in volume part would be associated with an increase both in back-scattering and in leading edge and with a decrease in height). Possible temperature effects will now be examined. The Done C temperature record (near the single track studied in section 1) does not display the same behaviour as the altimetric observation, neither in phase nor in amplitude, even if we take into account the propagation delay within the snowpack. The same conclusion is valid for brightness temperatures derived from the ERS1 radiometer and there are no correlations. In fact, during January and February, the evolution of the temperature is dominated by a continuous decrease on which second-order anomalies are superimposed. No similar trend is observed in the altimetric data. Finally, as observed by Brisset (1996), the difference between one summer and one winter 35 d cycle of ERS1 does not display any major signal, while the temperature difference is ~40 K. Hence, the temperature does not dominate the variations of the volume part of the radar echo observed here.
In addition lo analysing the rms variability of the echo parameters, it is also possible to map their temporal anomalies. The observed anomalies are significant and their spatial and temporal characteristics are similar to those of the meteorological perturbation, that is a few hundreds of kilometres and a few to tens of days (Seko and others, 1991). It should be noted that satellite under sampling does not allow adequate observation of meteorological displacement.
The observed correlation allows us to suggest that a realistic mechanism for varying the relative volume contribution to the altimetric echo is that meteorological events change the wind pattern and thus the surface micro-roughness. Because surface back-scattering is very sensitive to surface micro-roughness (Rémy and others, 1990), this may create fluctuations in surface back-scattering. The wind effect is complex. Kobayashi (1979) reported modification of the surface micro-roughness induced by cyclonic wind above the katabatic wind-formed patterns. However, we do not have sufficient elements to make more precise conclusions about the wind processes. Another possibility is that the hoar-frost growth and grain recrystallization, controlled by the rate of temperature change, alter the relative proportion of surface and sub-surface signals.. This possibility must be considered with care. The observed phenomena have to be reversible. The observed temperature record at Dome C does not show rates of temperature change correlated with the back-scatter changes. The better candidate for creating this signal remains wind processes.
2.3. Geographical signature of the phenomena
Although the large-scale variations show a common pattern for the three wave-form parameters, the effect of variation in back-scattering on both wave-form shape parameters produces a geographical signal. The high variations of back-scattering in West Antarctica at longitude 270° or 225° E induce high responses in leading-edge width at 270° E. The same effect is less impressive at longitude 225° E. This geographical behaviour of wave-form shape with respect to change in back-scattering is shown in Figure 6. Both maps show a coherent signal and are decorrelated with each other. While the leading edge is very sensitive to changes in σ°i near Tallos dome (155° E), the trailing edge shows less sensitivity. Conversely, near 135° E and 80° S, the leading edge is not very sensitive while the trailing edge is more sensitive. It is clear that this sensitivity is related to snowpack characteristics. These characteristics could therefore be deduced from an analysis of both maps using a waveform model to perform an inversion.

Fig. 6. Maps of the regression between (a) the back-scattering coefficient and the leading-edge width temporal variations (in gates dB-1, (b) the back-scattering coefficient and the trailing-edge slope temporal variations (in 10-4 Np gate dB-1).
3. Inversion of the Signal
3.1. Methodology
The retrieval of penetration-depth and volume-echo contributions to back-scattering will be performed following a two-step methodology. The first step will consist of establishing a theoretical model of leading-edge width and trailing-edge slope variations with respect to surface back-scattering changes by considering the volume-echo contribution to back-scattering. The second step will use the derived model to invert ERS1 data, as shown in Figure 6, to recover penetration-depth and volume-echo contributions to back-scattering over Antarctica.
The numerical echo model as developed in Legrésy and Rémy (1997) is used. This echo model allows us to simulate wave forms from a finely digitized topography in order to have as realistic wave forms as possible, taking into account satellite characteristics (e.g. altitude and antenna patterns) and surface back-scattering (σs). Volume echo is included in the simulation using a simple model controlled by the contribution of a “one-gate equivalent layer” to back-scattering (σν), resulting from stratification and ice-grain scattering, and by the extinction through the snowpack (xe) or equivalently the penetration depth (dp)—resulting from absorption and ice-grain scattering. The output of this model includes wave forms, which are retracked in the same manner as data analysed in the previous sections. All the wave-form parameters are then recovered: σ°, leading-edge width and trailing-edge slope.
3.2. Modeling variations of wave-form parameters
Theoretical values of dTr/dσ° and dFl/ dσ° are computed by varying σs between 0.5 and 1.5 times the reference value (σref), and by keeping the volume echo constant with respect to this reference value. The variable σref is the surface back-scattering corresponding to the roughness configuration present from the internal layers. Fifty real topographic situations with roughness and sub-footprint topography have been averaged for each configuration (σs, ν, xe); this makes the result more relevant to the mapped data. When σ s is equal to σref, the same configuration of roughness and micro-roughness is considered at the surface and at the internal interfaces. The relations Tr(σ°) and Fl(σ°) are verified as being linear. The parameters are then processed for 50 different real topographic patterns and for couples (σν/σref; dp) ranging as (0-0.5; 0-20 m). The resulting diagrams are shown in Figure 7 where the total volume part increases from the lower left hand corner (no penetration and no volume scattering) up to the upper right hand corner (strong penetration and strong volume scattering). Both the trailing-edge slope and leading-edge width decrease (negative derivatives) while surface scattering increases. Surface-scattering fluctuations greatly affect the trailing-edge slope when the volume part is important but have less effect when the volume part is weak. Surface-scattering fluctuations have a strong effect on the leading-edge width. The fluctuations of both leading edge and trailing edge due to change in surface back-scattering exhibit a different behaviour with respect to volume-signal characteristics. This difference allows inversion of Figure 6a and b and the recovery of both volume-scattering and penetration depth.

Fig. 7. Theoretical regressions: (a) the back-scattering coefficient and the leading-edge width (in gates dB-1), (b) the back-scattering coefficient and the trailing-edge slope (in 10-4 Np gate-1 dB-1) obtained by varying the surface back-scattering for each of the volume-echo configurations.
3.3. Volume-scattering and penetration depth over Antarctica
A linear inverse process, using a classical least-squares minimization technique, produces the first global maps of σv/σref and dp (Fig. 8). Offsets between observed ERS1 data and the model are weighted by the standard deviation of the parameters in the dataset.

Fig. 8. Maps of (a) the penetration depth (m) of Ku radar waves inside the snowpack; (b) the volume contribution (back-scattering of one ~30 cm layer/mean surface back-scattering).
The penetration-depth values vary from 7 m within the continent to 13 m at a lower altitude. These values are in good agreement with some of the previous estimates. Ulaby and others (1986) listed penetration depths of about 10 m at 13 GHz into dry snow, with an 0.24 Mg m-3 density and an 0.5 mm ice grain-size, while Hofer and Mätzler (1980) predicted penetration depths of 7 m at 13 GHz. With the help of Seasat altimeter wave-form analysis, Ridley and Partington (1988) found a penetration depth of 8 m in a small area. Using Geosat altimeter data, Davis and Zwally (1993) found penetration depths varying from 5 to 10 m in a small area, north of 72° S in Wilkes Land. Both studies relied on waveform analysis but were not performed on a global scale. These estimates are limited by the wave-form averaging procedure and by limitation to flat regions. The error of penetration-depth estimation associated with the present method has been evaluated by two means: first, the error in regression calculation inferred by noise has been calculated. The correlation between this error of inputs and output is 2.7 x 10-2, indicating that there is no relation between this error on the inputs and the output of the inversion. Secondly, the initial values have been perturbed by a Monte-Carlo method. The map of the maximum error given by the Monte-Carlo method on the penetration depth (not displayed here) presents an homogeneous signal of the order of 3 m that can be associated with the inversion, Although the order of magnitude of the extinction calculated here is in accordance with the previous values, the results should be discussed as there are disagreements in the spatial distribution and interpretation.
4. Discussion
4.1. Penetration depth and ice grain-size
The extinction coefficient is due to losses by absorption and scattering (ke= ka + ks). Absorption is mostly controlled by the temperature (Reference MätzlerMätzler, 1987) and decreases from the coast to the dome. According to Reference MätzlerMätzler (1987), the uncertainty about the actual behaviour of the imaginary part of the dielectric constant of dry snow with respect to temperature is serious and limits the interpretation of the microwave signature. In any case, as the temperature decreases from the coast to the interior of the continent, the absorption should behave similarly.
Scattering is mostly controlled by grain-size. Gow (1969)discussed the depth-time-temperature relationships of ice-crystal growth. The behaviour with depth of crystal growth can be expressed as
where D and D0 are the equivalent size of the crystal at a depth z and at the surface, respectively, E is the activation energy (of the order of45 J mole-1), R is the gas constant, k0 is a constant, acc the accumulation rate and T is the temperature of the snowpack. It is the grain-size in the first few metres of firn that plays a significant role on the radar observation. Hence, there are two principal physical phenomena which have opposite effects. Higher temperatures cause the snow grains to grow quickly, whereas higher accumulation rates cause them to grow slowly. There are many other physical phenomena acting on the grain-size. For example, the wind may crush the snow grains (Reference ColbeckColbeck, 1980) and create smaller grains in low-accumulation regions. Using ground-traverse data from Mirny (66°33’ S, 93°01’E) to Vostok (78°28’ S, 106°49’ E), Surdyk and Fily (1993) showed that the grain-size increases from the coast to the dome. At such a scale, it can therefore be concluded that the accumulation rate is the dominant controlling factor of grain-size (and a fortiori the scattering coefficient), with a lower effect from temperature. The large-scale behaviour shown in Figure 8 suggests that geographical variations of the extinction coefficient are predominantly controlled by grain-size.
Following Comiso and others (1982), a constant absorption coefficient of 0.04 m -1 is assumed. The penetration-depth distribution gives a scattering coefficient varying from 0.03 to 0.16 m-1. Assuming a cubic dependence law between scattering coefficient and grain-size (Reference ZwallyZwally, 1977), the equivalent diameter of snow grains is found to vary from 0.6 mm in the plateau region to 0.34 mm at lower altitudes. In comparison, Surdyk and Fily (1993) reported grain-sizes ranging from 0.2 to 3 mm using a large dataset of observed values. In addition, they pointed out that the gradient ratio of brightness temperatures between two frequencies is linked to snow grain-size. The gradient-ratio map is obtained (see Fig. 9) from the ERS11 radiometer data which give brightness temperatures at the vertical incidence of 23.8 and 36.5 GHz. The lower the ratio, the greater the grain-size and, consequently, the greater the scattering and the lower the penetration depth. This map is consistent with the penetration-depth map in East Antarctica. This confirms that the extinction is mostly controlled by scattering through grain-size. However, this has not been verified in West Antarctica, where the higher temperature perturbs the gradient-ratio significance (Surdyk and Fily, 1993). In fact, higher temperature implies a higher temperature gradient in the snowpack that influences the gradient-ratio measurement.

Fig. 9. Map of the “gradient ratio” (in 1/1000) of brightness temperatures at 23.8 and 36.5GHz obtained with the ERS11 radiometer. This ratio is empirically found to be linked to the snow grain-size by Surdyk and Fily (1993).
Finally, the large-scale signal of the penetration depth of radar waves (in the Ku band) within the snowpack seems to be more controlled by accumulation rate than by temperature, as was assumed by Davis and Zwally (1993).
4.2. Volume contribution
The volume-contribution (back-scattering of one ~30cm layer/mean surface back-scattering) map displays values from 0.05 to 0.4. The volume signal may be due to scattering by ice grains (Ridley and Partington, 1988), yet internal stratification is found empirically to be the dominant effect acting on the altimetric wave forms (Rémy and others, 1995). In this case, volume contribution depends both on the internal stratification intensity and on the number of strata. The number of strata per depth unit is important when the accumulation rate is low. The weak stratification found in Wilkes Land (Reference GoodwinGoodwin, 1988) is due to the high accumulation rate in this region (Reference BromwichBromwich, 1988), while the higher stratification near domes is due to the low accumulation rate (Reference Davis and ZwallySurdy and Fily, 1993.
Internal stratification intensity is representative of the density contrast from one layer to another and shows considerable variations from one region to another. Various phenomena play a role in the firn stratification such as snow-drift (Takahashi and others, 1988) or wind crusts (Reference GoodwinGoodwin, 1991).
Reference Rott, Storm and MillerRott and others (1992a, Reference Rott, Storm and Millerb) reported internal density variations of 0.1 and 0.05 g cm-2 rms, respectively, each 5 cm in East Antarctica for two sites less than 100 km apart, showing the spatial variability of the stratification. The geographical signal of volume contribution, in general, does not show any coherent pattern, except in some areas. The fact that snow-pack characteristics depend on various climatic processes such as accumulation, temperature variations and snow-drifting may explain the poor geographical signature of this parameter.
4.3. Long-term ice-sheet volume survey
The strong temporal variability exhibited here has an important consequence on ice-sheet volume surveyed from temporal altimetric series. First, the short-scale signal must be corrected. It is possible to do this using the wave-form model, the snowpack characteristics and the measured leading-edge width. Figure 10 shows the error on the height measurement as derived here, for a mean 2.3 gates “surface” leading-edge width. Assuming a residual error of 10%, this yields a raw noise estimate of 10 cm. For a minimal required precision of 2 cm year-1, and for good sampling of seasonal effects, about 25 measurements per year are required, leading to a short repeatability of around 15 d, which is of the order of oceanic requirements. The future missions, being planned to have a larger repetition time, will make this problem critical Secondly, climatic change will probably produce long-term changes both in the accumulation rate and wind regime. These changes probably also have a seasonal signature as suggested by Van der Veen and Jezck (1993). The challenge will be to discriminate between real changes in ice volume and observation noise. The climatic survey of ice sheets must then be done with the help of time series of both altimetric height and altimetric parameters (e.g. back-scattering, leading-edge width and trailing-edge slope).
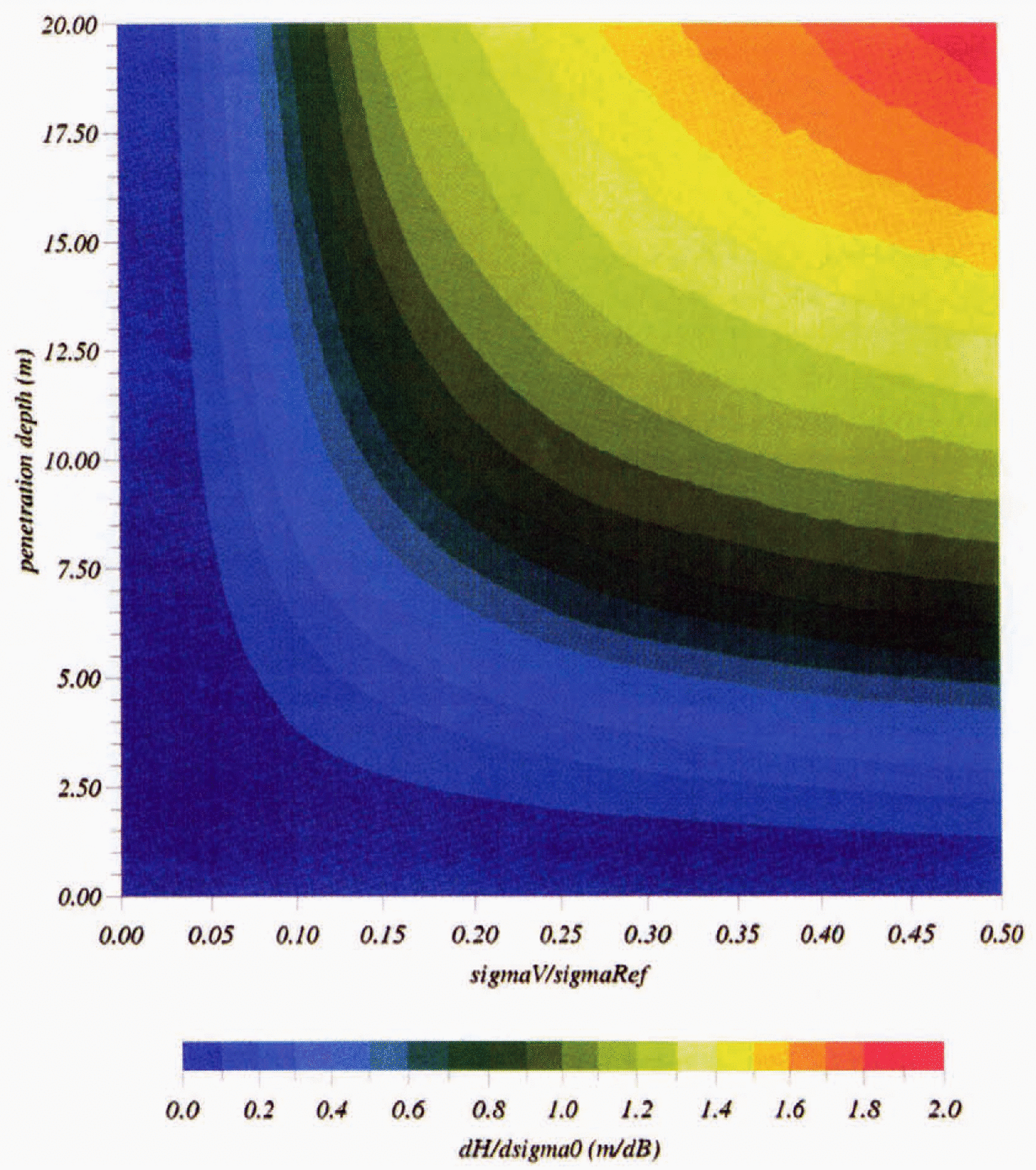
Fig. 10. Diagram of the height-variation artifact induced by surface-scattering variations in the presence of volume echo (in m dB-1 ).
Conclusion
We have presented here some important variations in the altimetric wave-form shape at short time-scales (a few days). There is strong circumstantial evidence that these variations are associated with meteorological events and that they create an artifact on the height measurement. These variations allows us to estimate snowpack characteristics, such as the penetration depth and volume back-scattering contribution front an inversion of a radar-echo model. The resulting map of penetration depth shows a strong coherent signal. The extinction of radar waves within the snowpack is found to be mostly linked with snow grain-size and temperature is a second-order effect. The survey of ice-sheet volume is therefore perturbed by this artifact. Given the rms variability measured on the 2 months long record (Fig. 5), the snowpack characteristics (deduced in Fig. 8) and the impact on height (Fig. 10), the resulting error that can be potentially reduced lies within 1 m in the western part of the ice sheet and more frequently around 40 cm in the eastern part. The survey of the altimetric wave-form shape will allow estimation of both ice-sheet mass balance and ice-sheet surface climate.
Acknowledgements
We thank P. Vincent from CNES for rigorously reviewing the paper and for constructive discussion. M. Fily (LGGE, Grenoble) is thanked for his useful comments. L. Eymard (CETP, Paris) is thanked for providing ERS1 radiometric data. B. Legrésy was funded by a CNES grant. Finally, we also thank J. Gunson (GRGS) for reviewing the English version of the paper.












