Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-18T08:40:00.996Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological bifurcations in the transition from two single vortices to a pair and a single vortex in the periodic wake behind an oscillating cylinder

Published online by Cambridge University Press:  08 April 2022

Anne R. Nielsen Open the ORCID record for Anne R. Nielsen [Opens in a new window] ,
Puneet S. Matharu Open the ORCID record for Puneet S. Matharu [Opens in a new window]  and
Morten Brøns Open the ORCID record for Morten Brøns [Opens in a new window]
Anne R. Nielsen
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800 Lyngby, Denmark
Puneet S. Matharu
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK
Morten Brøns*
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800 Lyngby, Denmark
*
†Email address for correspondence: mobr@dtu.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

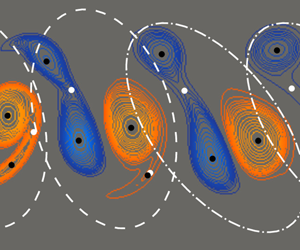
We explore the two-dimensional flow past a cylinder undergoing forced transversal oscillations with the aim of elucidating the evolution of the topology of the wake under variation of the forcing amplitude at a Reynolds number of 100. In particular, we study the change from two single vortices (2S mode) to a pair and a single vortex ($\text {P}+ \text {S}$ mode) being shed per period. Matharu et al. (J. Fluid Mech., vol. 918, 2021, p. A21) showed that a dynamical symmetry-breaking pitchfork bifurcation plays a key role in this transition. We show that in addition to this bifurcation, a number of topological bifurcations in the vorticity field occur, both on the symmetric 2S branch and on the asymmetric $\text {P}+ \text {S}$ branch. The topological bifurcations are cusp bifurcations where an extremum of vorticity is created or destroyed. To describe the effect of the topological bifurcations we introduce an extended symbolic classification of the wake modes to account for the spatial variations of the vortex patterns that occur in the transition process. We identify four amplitude values that define critical stages in the transition, and provide a complete qualitative picture of the transition from 2S to $\text {P}+ \text {S}$ mode. We confirm the robustness of the observed transition process by simulations at Reynolds number 80.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Wakes/Jets: Vortex streets Mathematical Foundations: Topological fluid dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A22
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aref, H., Stremler, M.A. & Ponta, F.L. 2006 Exotic vortex wakes-point vortex solutions. J. Fluids Struct. 22 (6–7), 929–940.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bishop, R.E.D., Hassan, A.Y. & Saunders, O.A. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 277 (1368), 51–75.Google Scholar
Blackburn, H.M. & Henderson, R.D. 1999 A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 385, 255–286.CrossRefGoogle Scholar
Blackburn, H.M., Marques, F. & Lopez, J.M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.CrossRefGoogle Scholar
Brika, D. & Laneville, A. 1993 Vortex-induced vibrations of a long flexible circular cylinder. J. Fluid Mech. 250, 481–508.CrossRefGoogle Scholar
Brøns, M. 2007 Streamline topology: patterns in fluid flows and their bifurcations. Adv. Appl. Mech. 41, 1–42.CrossRefGoogle Scholar
Brøns, M. & Bisgaard, A.V. 2010 Topology of vortex creation in the cylinder wake. Theor. Comput. Fluid Dyn. 24 (1–4), 299–303.CrossRefGoogle Scholar
Brøns, M., Jakobsen, B., Niss, K., Bisgaard, A. & Voigt, L.K. 2007 Streamline topology in the near wake of a circular cylinder at moderate Reynolds numbers. J. Fluid Mech. 584, 23–43.CrossRefGoogle Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2001 Forces and wake modes of an oscillating cylinder. J. Fluids Struct. 15 (3–4), 523–532.CrossRefGoogle Scholar
Dusek, J., Le Gal, P. & Fraunie, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
Dynnikova, G.Y., Dynnikov, Y.A., Guvernyuk, S.V. & Malakhova, T.V. 2021 Stability of a reverse Kármán vortex street. Phys. Fluids 33 (2), 024102.CrossRefGoogle Scholar
Gioria, R.S., Jabardo, P.J.S., Carmo, B.S. & Meneghini, J.R. 2009 Floquet stability analysis of the flow around an oscillating cylinder. J. Fluids Struct. 25 (4), 676–686.CrossRefGoogle Scholar
Godoy-Diana, R., Aider, J.-L. & Wesfreid, J.E. 2008 Transitions in the wake of a flapping foil. Phys. Rev. E 77 (1), 016308.CrossRefGoogle ScholarPubMed
Griffin, O.M. 1971 The unsteady wake of an oscillating cylinder at low Reynolds number. Trans. ASME E: J. Appl. Mech. 38 (4), 729–738.CrossRefGoogle Scholar
Heil, M. & Hazel, A.L. 2006 oomph-lib - an object-oriented multi-physics finite-element library. In Fluid–Structure Interaction (ed. M. Schäfer & H.-J. Bungartz), pp. 19–49. Springer.CrossRefGoogle Scholar
Heil, M., Rosso, J., Hazel, A.L. & Brøns, M. 2017 Topological fluid mechanics of the formation of the Kármán-vortex street. J. Fluid Mech. 812, 199–221.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Karasudani, T. & Funakoshi, M. 1994 Evolution of a vortex street in the far wake of a cylinder. Fluid Dyn. Res. 14 (6), 331–352.CrossRefGoogle Scholar
Leontini, J.S., Stewart, B.E., Thompson, M.C. & Hourigan, K. 2006 Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18 (6), 067101.CrossRefGoogle Scholar
Matharu, P.S., Hazel, A.L. & Heil, M. 2021 Spatio-temporal symmetry breaking in the flow past an oscillating cylinder. J. Fluid Mech. 918, A42.CrossRefGoogle Scholar
Morse, T.L. & Williamson, C.H.K. 2009 Fluid forcing, wake modes, and transitions for a cylinder undergoing controlled oscillations. J. Fluids Struct. 25 (4), 697–712.CrossRefGoogle Scholar
Noack, B.R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330.CrossRefGoogle Scholar
Ponta, F.L. & Aref, H. 2006 Numerical experiments on vortex shedding from an oscillating cylinder. J. Fluids Struct. 22 (3), 327–344.CrossRefGoogle Scholar
Sandulescu, M., Hernández-Garcìa, E., López, C. & Feudel, U. 2006 Kinematic studies of transport across an island wake, with application to the Canary Islands. Tellus A: Dyn. Meteorol. Oceanogr. 58 (5), 605–615.CrossRefGoogle Scholar
Schnipper, T., Andersen, A.P. & Bohr, T. 2009 Vortex wakes of a flapping foil. J. Fluid Mech. 633, 411–423.CrossRefGoogle Scholar
Shariff, K., Pulliam, T.H. & Ottino, J.M. 1991 A dynamical systems analysis of kinematics in the time-periodic wake of a circular cylinder. In Vortex Dynamics and Vortex Methoods (ed. C.R. Anderson & C. Greengard), Lectures in Applied Mathematics, vol. 28, pp. 613–646. American Mathematical Society.Google Scholar
Williamson, C.H.K. 1988 Defining a universal and continuous Strouhal-Reynolds number relationship for the laminar vortex shedding of a circular-cylinder. Phys. Fluids 31 (10), 2742–2744.CrossRefGoogle Scholar
Williamson, C.H.K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
Zienkiewicz, O.C. & Zhu, J.Z. 1992 The superconvergent patch recovery and a posteriori error estimates. Part 1: the recovery technique. Intl J. Numer. Meth. Engng 33 (7), 1331–1364.CrossRefGoogle Scholar