Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T09:16:16.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations

Published online by Cambridge University Press:  26 January 2016

Shriram Jagannathan  and
Diego A. Donzis
Shriram Jagannathan
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
Diego A. Donzis*
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: donzis@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We report results from direct numerical simulation (DNS) of stationary compressible isotropic turbulence at very-high resolutions and a range of parameters using a massively parallel code at Taylor Reynolds numbers (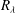$R_{{\it\lambda}}$) ranging from 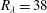$R_{{\it\lambda}}=38$ to 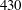$430$ and turbulent Mach numbers (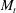$M_{t}$) ranging from 0.1 to 0.6 on up to 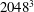$2048^{3}$ grid resolutions. A stationary state is maintained by a stochastic solenoidal forcing at the largest scales. The focus is on the mechanisms of energy exchanges, namely, dissipation, pressure-dilatation correlation and the individual contributing variables. Compressibility effects are studied by decomposing velocity and pressure fields into solenoidal and dilatational components. We suggest a critical turbulent Mach number at about 0.3 that separate two different flow regimes – only at Mach numbers above this critical value do we observe dilatational effects to affect the flow behaviour in a qualitative manner. The equipartition of energy between the dilatational components of kinetic and potential energy, originally proposed for decaying flows at low 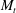$M_{t}$, presents significant scatter at low 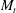$M_{t}$, but appears to be valid at high 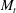$M_{t}$ for stationary flows, which is explained by the different role of dilatational pressure in decaying and stationary flows, and at low and high 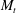$M_{t}$. While at low 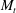$M_{t}$ pressure possesses characteristics of solenoidal pressure, at high 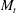$M_{t}$ it behaves in similar ways to dilatational pressure, which results in significant changes in the dynamics of energy exchanges. This also helps explain the observed qualitative change in the skewness of pressure at high 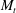$M_{t}$ reported in the literature. Regions of high pressure are found to be correlated with regions of intense local expansions. In these regions, the density–temperature correlation is also seen to be relatively high. Classical scaling laws for low-order moments originally proposed for incompressible turbulence appear to be only weakly affected by compressibility for the range of 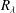$R_{{\it\lambda}}$ and 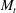$M_{t}$ investigated.

JFM classification

Turbulent Flows: Compressible turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 789 , 25 February 2016 , pp. 669 - 707
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bataille, F., Zhou, Y. & Bertoglio, J. P.1997 Energy transfer and triadic interactions in compressible turbulence. Tech. Rep. Defense Technical Information Center Document.Google Scholar
Bertoglio, J. P., Bataille, F. & Marion, J. D. 2001 Two-point closures for weakly compressible turbulence. Phys. Fluids 13, 290–310.CrossRefGoogle Scholar
Bertsch, R. L., Suman, S. & Girimaji, S. S. 2012 Rapid distortion analysis of high Mach number homogeneous shear flows: characterization of flow-thermodynamics interaction regimes. Phys. Fluids 24 (12), 125106.CrossRefGoogle Scholar
Blaisdell, G. A., Mansour, N. N. & Reynolds, W. C. 1993 Compressibility effects on the growth and structure of homogeneous turbulent shear flow. J. Fluid Mech. 256 (1), 443–485.CrossRefGoogle Scholar
Blaisdell, G. A. & Zeman, O. 1992 Investigation of the dilatational dissipation in compressible homogeneous shear flow. In Studying Turbulence Using Numerical Simulation Databases (ed. Spinks, D.), Center for Turbulence Research Summer Program. Center for Turbulence Research, Stanford University, 231–245.Google Scholar
Chu, B. T. & Kovásznay, L. S. G. 1958 Non-linear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3 (05), 494–514.CrossRefGoogle Scholar
Cook, A. W., Cabot, W. H., Williams, P. L., Miller, B. J., Supinski, B. R., de Yates, R. K. & Welcome, M. L. 2005 Tera-scalable algorithms for variable-density elliptic hydrodynamics with spectral accuracy. In Proceedings of the 2005 ACM/IEEE Conference on Supercomputing, SC’05 1, p. 60. IEEE Computer Society.CrossRefGoogle Scholar
Dastgeer, S. & Zank, G. P. 2005 Turbulence in nearly incompressible fluids: density spectrum, flows, correlations and implication to the interstellar medium. Nonlinear Process. Geophys. 12, 139–148.CrossRefGoogle Scholar
Donzis, D. A. & Jagannathan, S. 2013a Fluctuations of thermodynamic variables in stationary compressible turbulence. J. Fluid Mech. 733, 221–244.CrossRefGoogle Scholar
Donzis, D. A. & Jagannathan, S. 2013b On the relation between small-scale intermittency and shocks in turbulent flows. Procedia IUTAM 9, 3–15.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2012 Some results on the Reynolds number scaling of pressure statistics in isotropic turbulence. Physica D 241, 164–168.CrossRefGoogle Scholar
Donzis, D. A., Yeung, P. K. & Pekurovsky, D. 2008a Turbulence simulations on $O(10^{4})$ processors. In TeraGrid 2008 Conference, Las Vegas, NV.Google Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008b Dissipation and enstrophy in isotropic turbulence: scaling and resolution effects in direct numerical simulations. Phys. Fluids 20, 045108.CrossRefGoogle Scholar
Erlebacher, G., Hussaini, M. Y., Kreiss, H. O. & Sarkar, S. 1990 The analysis and simulation of compressible turbulence. Theor. Comput. Fluid Dyn. 2 (2), 73–95.CrossRefGoogle Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 16, 257–278.CrossRefGoogle Scholar
Fauchet, G. & Bertoglio, J. P. 1998 An analytical expression for the spectrum of compressible turbulence in the low Mach number limit. In Advances in Turbulence VII (ed. Frisch, U.), Fluid Mechanics and Its Applications, vol. 46, pp. 317–320. Springer.CrossRefGoogle Scholar
Hamba, F. 1999 Effects of pressure fluctuations on turbulence growth in compressible homogeneous shear flow. Phys. Fluids 11, 1623.CrossRefGoogle Scholar
Holzer, M. & Siggia, E. 1993 Skewed, exponential pressure distributions from Gaussian velocities. Phys. Fluids A 5 (10), 2525–2532.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Jagannathan, S. & Donzis, D. A. 2012 Massively parallel direct numerical simulations of forced compressible turbulence: a hybrid MPI/OpenMP approach. In XSEDE 2012 Conference, Chicago, IL, ACM.Google Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15 (2), L21–L24.CrossRefGoogle Scholar
Kida, S. & Orszag, S. A. 1990 Energy and spectral dynamics in forced compressible turbulence. J. Sci. Comput. 5, 85–125.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kovasznay, L. S. G. 1953 Turbulence in supersonic flow. J. Aeronaut. Sci. 20 (10), 657–674.CrossRefGoogle Scholar
Kraichnan, R. H. 1955 On the statistical mechanics of an adiabatically compressible fluid. J. Acoust. Soc. Am. 27 (3), 438–441.CrossRefGoogle Scholar
Lee, K. & Girimaji, S. S. 2013 Flow-thermodynamics interactions in decaying anisotropic compressible turbulence with imposed temperature fluctuations. Theor. Comput. Fluid Dyn. 27 (1–2), 115–131.CrossRefGoogle Scholar
Lee, K., Girimaji, S. S. & Kerimo, J. 2009 Effect of compressibility on turbulent velocity gradients and small-scale structure. J. Turbul. 10, 1–18.CrossRefGoogle Scholar
Lee, S., Lele, S. K. & Moin, P. 1991 Eddy shocklets in decaying compressible turbulence. Phys. Fluids 3, 657–664.CrossRefGoogle Scholar
Lee, S., Lele, S. K. & Moin, P. 1993 Direct numerical simulation of isotropic turbulence interacting with a weak shock wave. J. Fluid Mech. 251, 533–562.CrossRefGoogle Scholar
Lele, S. K. 1992 Compact finite-difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
Lele, S. K. 1994 Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 26, 211–254.CrossRefGoogle Scholar
Livescu, D., Jaberi, F. A. & Madnia, C. K. 2002 The effects of heat release on the energy exchange in reacting turbulent shear flow. J. Fluid Mech. 450 (-1), 35–66.CrossRefGoogle Scholar
Lv, X-G. & Le, J. 2008 A note on solving nearly penta-diagonal linear systems. Appl. Maths Comput. 204, 707–712.CrossRefGoogle Scholar
Miura, H. & Kida, S. 1995 Acoustic energy exchange in compressible turbulence. Phys. Fluids 7 (7), 1732–1742.CrossRefGoogle Scholar
Overholt, M. R. & Pope, S. B. 1998 A deterministic forcing scheme for direct numerical simulations of turbulence. Comput. Fluids 27, 11–28.CrossRefGoogle Scholar
Pearson, B. R., Yousef, T. A., Haugen, N. E. L., Brandenburg, A. & Krogstad, P. 2004 Delayed correlation between turbulent energy injection and dissipation. Phys. Rev. E 70 (5), 056301.CrossRefGoogle ScholarPubMed
Petersen, M. R. & Livescu, D. 2010 Forcing for statistically stationary compressible isotropic turbulence. Phys. Fluids 22, 116101.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2004 Direct numerical simulations of isotropic compressible turbulence: influence of compressibility on dynamics and structures. Phys. Fluids 16, 4386–4407.CrossRefGoogle Scholar
Pumir, A. 1994 A numerical study of pressure fluctuations in three-dimensional, incompressible, homogeneous, isotropic turbulence. Phys. Fluids 6, 2071.CrossRefGoogle Scholar
Ristorcelli, J. R. 1997 A pseudo-sound constitutive relationship for the dilatational covariances in compressible turbulence. J. Fluid Mech. 347, 37–70.CrossRefGoogle Scholar
Rosales, C. & Meneveau, C. 2005 Linear forcing in numerical simulations of isotropic turbulence: physical space implementations and convergence properties. Phys. Fluids 17, 095106.CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Samtaney, R., Pullin, D. I. & Kosovic, B. 2001 Direct numerical simulation of decaying compressible turbulence and shocklet statistics. Phys. Fluids 13, 1415.CrossRefGoogle Scholar
Sarkar, S. 1992 The pressure-dilatation correlation in compressible flows. Phys. Fluids A 4 (12), 2674–2682.CrossRefGoogle Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 227, 473–493.CrossRefGoogle Scholar
Schmidt, W., Hillebrandt, W. & Niemeyer, J. C. 2006 Numerical dissipation and the bottleneck effect in simulations of compressible isotropic turbulence. Comput. Fluids 35 (4), 353–371.CrossRefGoogle Scholar
Shivamoggi, B. K. 1995 Multifractal scaling at the kolmogorov microscale in fully developed compressible turbulence. Ann. Phys. 243 (1), 177–191.CrossRefGoogle Scholar
Shivamoggi, B. K. 1997 Equilibrium statistical mechanics of compressible isotropic turbulence. Europhys. Lett. 38 (9), 657–662.CrossRefGoogle Scholar
Shivamoggi, B. K. 1995 Erratum and addendum to ‘Multi-fractal scaling at the Kolmogorov microscale in fully developed compressible turbulence’ [Ann. Phys. 243 (1995), 177–191]. Ann. Phys. 318 (2), 497–499.Google Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy-dissipation rate. Phys. Fluids 27, 1048–1051.CrossRefGoogle Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulations of isotropic turbulence. Phys. Fluids 11, 1208–1220.CrossRefGoogle Scholar
Vreman, A. W., Sandham, N. D. & Luo, K. H. 1996 Compressible mixing layer growth rate and turbulence characteristics. J. Fluid Mech. 320 (1), 235–258.CrossRefGoogle Scholar
Wang, J., Shi, Y., Wang, L. P., Xiao, Z., He, X. T. & Chen, S. 2012 Effect of compressibility on the small-scale structures in isotropic turbulence. J. Fluid Mech. 1 (1), 1–44.Google Scholar
Wang, J., Shi, Y., Wang, L.-P., Xiao, Z., He, X. & Chen, S. 2011 Effect of shocklets on the velocity gradients in highly compressible isotropic turbulence. Phys. Fluids 23, 125103.CrossRefGoogle Scholar
Wang, J., Wang, L.-P., Xiao, Z., Shi, Y. & Chen, S. 2010 A hybrid numerical simulation of isotropic compressible turbulence. J. Comput. Phys. 229, 5257–5279.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2007 Inertial-range intermittency and accuracy of direct numerical simulation for turbulence and passive scalar turbulence. J. Fluid Mech. 590, 117–146.CrossRefGoogle Scholar
Yeung, P. K. & Brasseur, J. G. 1991 The response of isotropic turbulence to isotropic and anisotropic forcing at the large scales. Phys. Fluids 3, 884–897.CrossRefGoogle Scholar
Zeman, O. 1990 Dilatation dissipation: the concept and application in modeling compressible mixing layers. Phys. Fluids A 2 (2), 178–188.CrossRefGoogle Scholar