Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T11:51:23.509Z Has data issue: false hasContentIssue false
  • English
  • Français

The pollution of pristine material in compressible turbulence

Published online by Cambridge University Press:  01 May 2012

Liubin Pan ,
Evan Scannapieco  and
John Scalo
Liubin Pan*
Affiliation:
School of Earth and Space Exploration, Arizona State University, PO Box 871404, Tempe, AZ 85287, USA
Evan Scannapieco
Affiliation:
School of Earth and Space Exploration, Arizona State University, PO Box 871404, Tempe, AZ 85287, USA
John Scalo
Affiliation:
Department of Astronomy, University of Texas, Austin, TX 78712, USA
*
†Email address for correspondence: liubin.pan@asu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The first generation of stars had very different properties than later stellar generations, as they formed from a ‘pristine’ gas that was completely free of heavy elements. Normal star formation took place only after the first stars had polluted the surrounding turbulent interstellar gas, increasing its local heavy-element mass concentration, 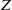, beyond a ‘critical’ threshold value, 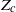(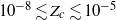). Motivated by this astrophysical problem, we investigate the fundamental physics of the pollution of pristine fluid elements in statistically homogeneous and isotropic compressible turbulence. Turbulence stretches the pollutants, produces concentration structures at small scales, and brings the pollutants and the unpolluted flow in closer contact. The pristine material is polluted when exposed to the pollutant sources or the fluid elements polluted by previous mixing events. Our theoretical approach employs the probability distribution function (p.d.f.) method for turbulent mixing, as the fraction of pristine mass corresponds to the low tail of the density-weighted concentration p.d.f. We adopt a number of p.d.f. closure models and derive evolution equations for the pristine fraction from the models. To test and constrain the prediction of theoretical models, we conduct numerical simulations for decaying passive scalars in isothermal turbulent flows with Mach numbers of 0.9 and 6.2, and compute the mass fraction, 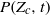, of the flow with 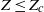. In the Mach 0.9 flow, the evolution of 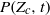is well-described by a continuous convolution model and goes as 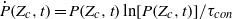, if the mass fraction of the polluted flow is larger than 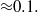If the initial pollutant fraction is smaller than 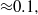an early phase exists during which the pristine fraction follows an equation derived from a nonlinear integral model: 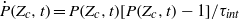. The time scales 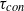and 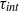are measured from our simulations. When normalized to the flow dynamical time, the decay of 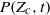in the Mach 6.2 flow is slower than at Mach 0.9 because the time scale for scalar variance decay is slightly larger and the low tail of the concentration p.d.f. broadens with increasing Mach number. We show that 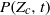in the Mach 6.2 flow can be well fitted using a formula from a generalized version of the self-convolution model.

JFM classification

Turbulent Flows: Compressible turbulence Turbulent Flows: Turbulence modelling Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 700 , 10 June 2012 , pp. 459 - 489
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abel, T., Bryan, G. L. & Norman, M. L. 2000 The formation and fragmentation of primordial molecular clouds. Astrophys. J. 540, 39–44.CrossRefGoogle Scholar
2. Bromm, V., Coppi, P. S. & Larson, R. B. 2002 The formation of the first stars. I. The primordial star-forming cloud. Astrophys. J. 564, 23–51.CrossRefGoogle Scholar
3. Bromm, V. & Loeb, A. 2003 The formation of the first low-mass stars from gas with low carbon and oxygen abundances. Nature 654, 29–32.Google Scholar
4. Caffau, E., Bonifacio, P., Francois, P., Sbordone, L., Monaco, L., Spite, M., Spite, F., Ludwig, H.-G., Cayrel, R., Zaggia, S., Hammer, F., Randich, S., Molaro, P. & Hill, V. 2011 An extremely primitive star in the Galactic halo. Nature 477, 67–69.CrossRefGoogle ScholarPubMed
5. Cayrel, R., Depagne, E., Spite, M., Hill, V., Spite, F., Francois, P., Plez, B., Beers, T., Primas, F., Andersen, J., Barbuy, B., Bonifacio, P., Molaro, P. & Nordstrom, B. 2004 First stars V-abundance patterns from C to Zn and supernova yields in the early Galaxy. Astron. Astrophys. 416, 1117–1138.CrossRefGoogle Scholar
6. Chen, H., Chen, S. & Kraichnan, R. H. 1989 Probability distribution of a stochastically advected scalar field. Phys. Rev. Lett. 425, 812–814.Google Scholar
7. Colella, P. & Glaz, H. M. 1985 Efficient solution algorithms for the Riemann problem for real gases. J. Comput. Phys. 59, 264–289.CrossRefGoogle Scholar
8. Colella, P. & Woodward, P. R. 1984 The Piecewise Parabolic Method (PPM) for gas-dynamical simulations. J. Comput. Phys. 54, 174–201.CrossRefGoogle Scholar
9. Corrsin, R. L. 1951 On the spectrum of isotropic temperature fluctuations in isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
10. Curl, S. 1963 Dispersed phase mixing: I. Theory and effects in simple reactors. AIChE J. 9, 175–181.CrossRefGoogle Scholar
11. Dopazo, C. 1979 Relaxation of initial probability density functions in the turbulent convection of scalar fields. Phys. Fluids 22, 20–30.CrossRefGoogle Scholar
12. Dopazo, C. & O’Brien, E. E. 1974 An approach to the autoignition of a turbulent mixture. Acta Astron. 1, 1239–1266.CrossRefGoogle Scholar
13. Dopazo, C., Valino, L. & Fueyo, N. 1997 Statistical description of the turbulent mixing of scalar fields. Intl J. Mod. Phys. B 11, 2975–3014.CrossRefGoogle Scholar
14. Duplat, J. & Villermaux, E. 2008 Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51–86.CrossRefGoogle Scholar
15. Fox, R. O. 2003 Computational Models for Turbulent Reacting Flows. Cambridge University Press.CrossRefGoogle Scholar
16. Frebel, A., Collet, R., Eriksson, K., Christlieb, N. & Aoki, W. 2008 HE 1327-2326, an unevolved star with . II. New 3D-1D corrected abundances from a very large telescope UVES spectrum. Astrophys. J. 684, 588–602.CrossRefGoogle Scholar
17. Fryxell, B., Müller, E. & Arnett, D. 1989 Computation of multi-dimensional flows with non-uniform composition. In Proceedings of the 5th Workshop on Nuclear Astrophysics, vol. 5. pp. 100–102. ARI.Google Scholar
18. Fryxell, B., Olson, K., Ricker, P., Timmes, F. X., Zingale, M., Lamb, D. Q., MacNeice, P., Rosner, R., Truran, J. W. & Tufo, H. 2000 FLASH: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophys. J. Suppl. Ser. 131, 273–334.CrossRefGoogle Scholar
19. Girimaji, S. S. 1992 A mapping closure for turbulent scalar mixing using a time-evolving reference field. Phys. Fluids A 4, 2875.CrossRefGoogle Scholar
20. Greif, T. H., Johnson, J. L., Klessen, R. S. & Bromm, V. 2008 The first galaxies: assembly, cooling and the onset of turbulence. Mon. Not. R. Astron. Soc. 387, 1021–1036.CrossRefGoogle Scholar
21. Haworth, D. C. 2010 Progress in probability density function methods for turbulent reacting flows. Prog. Energy Combust. Sci. 36, 168–259.CrossRefGoogle Scholar
22. He, G.-W. & Zhang, Z.-F. 2004 Two-point closure strategy in the mapping closure approximation approach. Phys. Rev. E 70, 036309.CrossRefGoogle ScholarPubMed
23. Ievlev, V. M. 1973 Equations for the finite-dimensional probability distributions of pulsating variables in a turbulent flow. Dokl. Akad. Nauk SSSR 208, 1044–1047.Google Scholar
24. Janicka, J., Kolbe, W. & Kollmann, W. 1979 Closure of the transport equation for the probability density funcfion of turbulent scalar fields. J. Non-Equilib. Thermodyn. 4, 47–66.CrossRefGoogle Scholar
25. Jimenez, R. & Haiman, Z. 2006 Significant primordial star formation at redshifts . Nature 440, 501–504.CrossRefGoogle Scholar
26. Kollmann, W. 1990 The pdf approach to turbulent flow. Theor. Comput. Fluid Dyn. 1, 249–285.CrossRefGoogle Scholar
27. Lundgren, T. S. 1967 Distribution function in the statistical theory of turbulence. Phys. Fluids 12, 485–497.CrossRefGoogle Scholar
28. Monin, A. S. 1967 Equations for finte dimensional probability distributions of a field of turbulence. Dokl. Akad. Nauk SSSR 177, 1036–1038.Google Scholar
29. Nagao, T., Sasaki, S. S., Maiolino, R., Grady, C., Kashikawa, N., Ly, C., Malkan, M. A., Motohara, K., Murayama, T., Schaerer, D., Shioya, Y. & Taniguchi, Y. 2008 A photometric survey for Ly-He II dual emitters: searching for Population III stars in high-redshift galaxies. Astrophys. J. 680, 100–109.CrossRefGoogle Scholar
30. Novikov, E. A. 1967 Kinetic equations for a vortex field. Dokl. Akad. Nauk SSSR 177, 299–301.Google Scholar
31. Obrien, E. E. 1980 The probability density function (PDF) approach to reacting turbulent flows. In Turbulent Reacting Flows (ed. Libby, P. A. & Williams, F. A. ). pp. 185–218. Springer.CrossRefGoogle Scholar
32. Obukhov, A. M. 1949 The structure of the temperature eld in a turbulent flow. Izv. Akad. Nauk SSSR Ser. Geogr. Geophys. 13, 58–69.Google Scholar
33. Omukai, K., Tsuribe, T., Schneider, R. & Ferrara, A. 2005 Thermal and fragmentation properties of star-forming slouds in low-metallicity environments. Astrophys. J. 626, 627–643.CrossRefGoogle Scholar
34. Pan, L. & Scalo, J. 2007 Mixing of primordial gas in Lyman Break Galaxies. Astrophys. J. Lett. 654, 29–32.CrossRefGoogle Scholar
35. Pan, L. & Scannapieco, E. 2010 Mixing in supersonic turbulence. Astrophys. J. 721, 1765–1782.CrossRefGoogle Scholar
36. Pan, L. & Scannapieco, E. 2011 Passive scalar structures in supersonic turbulence. Phys. Rev. E 83, 045302.CrossRefGoogle ScholarPubMed
37. Pope, S. B. 1976 The probability approach to the modelling of turbulent reacting flows. Combust. Flame 27, 299–312.CrossRefGoogle Scholar
38. Pope, S. B. 1982 An improved turbulent mixing model. Combust. Sci. Technol. 28, 131–145.CrossRefGoogle Scholar
39. Pope, S. B. 1985 PDF methods for turbulent reactive flows. Prog. Energy Combust. Sci. 11, 119–192.CrossRefGoogle Scholar
40. Pope, S. B. 1991 Mapping closures for turbulent mixing and reaction. Theor. Comput. Fluid Dyn. 2, 255–270.CrossRefGoogle Scholar
41. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
42. Pumir, A., Shraiman, B. I. & Siggia, E. D. 1991 Exponential tails and random advection. Phys. Rev. Lett. 66 (23), 2984–2987.CrossRefGoogle ScholarPubMed
43. Scannapieco, E., Madau, P., Woosley, S., Heger, A. & Ferrara, A. 2005 The detectability of pair-production supernovae at . Astrophys. J. 633, 1031–1041.CrossRefGoogle Scholar
44. Scannapieco, E., Schneider, R. & Ferrara, A. 2003 The detectability of the first stars and their cluster enrichment signatures. Astrophys. J. 589, 35–52.CrossRefGoogle Scholar
45. Schaerer, D. 2002 On the properties of massive Population III stars and metal-free stellar populations. Astron. Astrophys. 382, 28–42.CrossRefGoogle Scholar
46. Valino, L. & Dopazo, C. 1990 A binomial sampling model for scalar turbulent mixing. Phys. Fluids A 2, 1204–1212.CrossRefGoogle Scholar
47. Venaille, A. & Sommeria, J. 2007 A dynamical equation for the distribution of a scalar advected by turbulence. Phys. Fluids 19, 028101.CrossRefGoogle Scholar
48. Venaille, A. & Sommeria, J. 2008 Is turbulent mixing a self-convolution process? Phys. Rev. Lett. 100, 234506.CrossRefGoogle ScholarPubMed
49. Veynante, D. & Vervisch, L. 2002 Turbulent combustion modelling. Prog. Energy Combust. Sci. 28, 193–266.CrossRefGoogle Scholar
50. Villermaux, E. & Duplat, J. 2003 Mixing as an aggregation process? Phys. Rev. Lett. 91, 184501.CrossRefGoogle ScholarPubMed
51. Villermaux, E., Stroock, A. D. & Stone, H. A. 2008 Bridging kinematics and concentration content in a chaotic micromixer. Phys. Rev. E 77, 015301(R).CrossRefGoogle Scholar
52. Walker, T. P., Steigman, G., Kang, H.-S., Schramm, D. M. & Olive, K. A. 1991 Primordial nucleosynthesis redux. Astrophys. J. 376, 51–69.CrossRefGoogle Scholar
53. Wise, J. H., Turk, M. J. & Abel, T. 2008 Resolving the formation of protogalaxies. II. Central gravitational collapse. Astrophys. J. 682, 745–757.CrossRefGoogle Scholar