Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T11:51:04.720Z Has data issue: false hasContentIssue false
  • English
  • Français

On the scaling of turbulence in a high Reynolds number tidal flow

Published online by Cambridge University Press:  25 March 2021

I.A. Milne Open the ORCID record for I.A. Milne [Opens in a new window] ,
J.M.R. Graham Open the ORCID record for J.M.R. Graham [Opens in a new window]  and
D.S. Coles Open the ORCID record for D.S. Coles [Opens in a new window]
I.A. Milne*
Affiliation:
Oceans Graduate School, The University of Western Australia, Crawley6009, Australia
J.M.R. Graham
Affiliation:
Department of Aeronautics, Imperial College London, SW7 2AZ, UK
D.S. Coles
Affiliation:
School of Engineering, Computing and Mathematics, University of Plymouth, PlymouthPL4 8AA, UK SIMEC Atlantis Energy, EdinburghEH3 9QG, UK
*
†Email address for correspondence: ian.milne@uwa.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

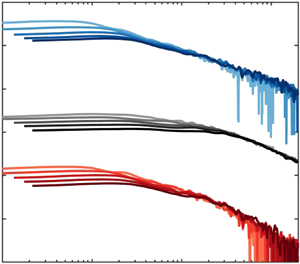
Data from an energetic tidal flow are used to investigate the appropriateness of the classical scaling of wall turbulence for very high Reynolds numbers and fully rough conditions. The boundary layer occupied the entire channel depth and the Reynolds numbers were several orders of magnitude larger than typically attained in the laboratory. Profiles of the mean velocity, turbulence quantities and spectra exhibit consistencies with the wall-similarity hypothesis and the attached-eddy model, as well as the universality of the near-wall turbulence structure for geophysical flows. The wall-normal velocity spectra and intensities near the free surface are also strongly attenuated at low wavenumbers, consistent with the constraints imposed by any boundary which may be approximated as a plane slip surface. The results can be used to inform the development of turbulence inflow models for assessing the dynamic loading on tidal turbines and the layout of tidal energy farms.

JFM classification

Geophysical and Geological Flows: Ocean processes Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A104
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bowden, K.F. & Ferguson, S.R. 1980 Variation with height of the turbulence in a tidally-induced bottom boundary layer. In Marine Turbulence, Proceedings of the 11th International Liege Colloquium on Ocean Hydrodynamics (ed. J. Nihoul), pp. 258–286. Elsevier Science.CrossRefGoogle Scholar
Cardoso, A.H., Graf, W.H. & Gust, G. 1989 Uniform flow in a smooth open channel. J. Hydraul. Res. 27 (5), 603–616.CrossRefGoogle Scholar
Grant, H.L., Stewart, R.W. & Moilliet, A. 1962 Turbulence spectra from a tidal channel. J. Fluid Mech. 12 (2), 241–268.CrossRefGoogle Scholar
Gross, T.F. & Nowell, A.R.M. 1985 Spectral scaling in a tidal boundary layer. J. Phys. Oceanogr. 15, 496–508.2.0.CO;2>CrossRefGoogle Scholar
Guerra, M. & Thomson, J. 2017 Turbulence measurements from five-beam acoustic Doppler current profilers. J. Atmos. Ocean. Technol. 34 (6), 1267–1284.CrossRefGoogle Scholar
Handler, R.A., Swean, T.F., Leighton, R.I. & Swearingen, J.D. 1993 Length scales and the energy balance for turbulence near a free surface. AIAA J. 31 (11), 1998–2007.CrossRefGoogle Scholar
Hunt, J.C.R. & Graham, J.M.R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84 (2), 209–235.CrossRefGoogle Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21.Google Scholar
Kolmogorov, A.N. 1941 b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kunkel, G.J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.CrossRefGoogle Scholar
Lien, R.-C. & Sanford, T.B. 2000 Spectral characteristics of velocity and vorticity fluxes in an unstratified turbulent boundary layer. J. Geophys. Res. 105 (C4), 8659–8672.CrossRefGoogle Scholar
Lohrmann, A., Hackett, B. & Røed, L.P. 1990 High resolution measurements of turbulence, velocity and stress using a pulse-to-pulse coherent sonar. J. Atmos. Ocean. Technol. 7, 19–37.2.0.CO;2>CrossRefGoogle Scholar
Lu, Y. & Lueck, R.G. 1999 Using a broadband ADCP in a tidal channel. Part II: turbulence. J. Atmos. Ocean. Technol. 16, 1568–1579.2.0.CO;2>CrossRefGoogle Scholar
Marusic, I. & Kunkel, G.J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.CrossRefGoogle Scholar
Marusic, I., Monty, J.P., Hultmark, M. & Smits, A.J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Marusic, I. & Perry, A.E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
McMillan, J.M. & Hay, A.E. 2017 Spectral and structure function estimates of turbulence dissipation rates in a high-flow tidal channel using broadband ADCPs. J. Atmos. Ocean. Technol. 34 (1), 5–20.CrossRefGoogle Scholar
McMillan, J.M., Hay, A.E., Lueck, R.G. & Wolk, F. 2016 Rates of dissipation of turbulent kinetic energy in a high Reynolds number tidal channel. J. Atmos. Ocean. Technol. 33, 817–837.CrossRefGoogle Scholar
Milne, I.A., Day, A.H., Sharma, R.N. & Flay, R.G.J. 2016 The characterisation of the hydrodynamic loads on tidal turbines due to turbulence. Renew. Sust. Energy Rev. 56, 851–864.CrossRefGoogle Scholar
Milne, I.A., Sharma, R.N. & Flay, R.G.J. 2017 The structure of turbulence in a rapid tidal flow. Proc. R. Soc. A 473, 20170295.CrossRefGoogle Scholar
Milne, I.A., Sharma, R.N., Flay, R.G.J. & Bickerton, S. 2013 Characteristics of the turbulence in the flow at a tidal stream power site. Phil. Trans. R. Soc. A 371, 20120196.CrossRefGoogle Scholar
Osalusi, E., Side, J. & Harris, R. 2009 Reynolds stress and turbulence estimates in bottom boundary layer of Fall of Warness. Intl Commun. Heat Mass Transfer 36 (5), 412–421.CrossRefGoogle Scholar
Perry, A.E., Henbest, S. & Chong, M.S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Raupach, M.R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.CrossRefGoogle Scholar
Raupach, M.R., Antonia, R.A. & Rajagopalan, S.S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.CrossRefGoogle Scholar
RDI 2017 Velocity Software User's Guide. Teledyne RD Instruments, Inc.Google Scholar
Rippeth, T.P., Simpson, J.H., Williams, E. & Inall, M.E. 2003 Measurement of the rates of production and dissipation of turbulent kinetic energy in an energetic tidal flow: Red Wharf Bay revisited. J. Phys. Oceanogr. 33 (9), 1889–1901.2.0.CO;2>CrossRefGoogle Scholar
Saddoughi, S.G. & Veeravalli, S.V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Schultz, M.P. & Flack, K.A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.CrossRefGoogle Scholar
Squire, D.T., Morrill-Winter, C., Hutchins, N., Schultz, M.P., Klewicki, J.C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.CrossRefGoogle Scholar
Stacey, M.T., Monismith, S.G. & Burau, J.R. 1999 Measurements of Reynolds stress profiles in unstratified tidal flow. J. Geophys. Res. 104 (C5), 10933–10949.CrossRefGoogle Scholar
Taylor, G.I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.Google Scholar
Thiébaut, M., Filipot, J.-F., Maisondieu, C., Damblans, G., Duarte, R., Droniou, E. & Guillou, S. 2020 Assessing the turbulent kinetic energy budget in an energetic tidal flow from measurements of coupled ADCPs. Phil. Trans. R. Soc. A 378, 20190496.CrossRefGoogle Scholar
Thomas, N.H. & Hancock, P.E. 1977 Grid turbulence near a moving wall. J. Fluid Mech. 82 (3), 481–496.CrossRefGoogle Scholar
Thomson, J., Polagye, B., Durgesh, V. & Richmond, M.C. 2012 Measurements of turbulence at two tidal energy sites in Puget Sound, WA. IEEE J. Ocean. Engng 37 (3), 363–374.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Vermeulen, B., Hoitink, A.J.F. & Sassi, M.G. 2011 Coupled ADCPs can yield complete Reynolds stress tensor profiles in geophysical surface flows. Geophys. Res. Lett. 38, L06406.CrossRefGoogle Scholar
Walter, R.K., Nidzieko, N.J. & Monismith, S.G. 2011 Similarity scaling of turbulence spectra and cospectra in a shallow tidal flow. J. Geophys. Res. 116, C10019.CrossRefGoogle Scholar
Williams, E. & Simpson, J.H. 2004 Uncertainties in estimates of Reynolds stress and TKE production rate using the ADCP variance method. J. Atmos. Ocean. Technol. 21 (2), 347–357.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J.C. & Coté, O.R. 1972 Cospectral similarity in the atmospheric surface layer. Q.J.R. Meteorol. Soc. 98, 590–603.CrossRefGoogle Scholar
Zedel, L. & Hay, A.E. 1999 A coherent Doppler profiler for high-resolution particle velocimetry in the ocean: laboratory measurements of turbulence and particle flux. J. Atmos. Ocean. Technol. 16 (8), 1102–1117.2.0.CO;2>CrossRefGoogle Scholar