Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-18T16:45:36.030Z Has data issue: false hasContentIssue false
  • English
  • Français

Law of the wall in an unstably stratified turbulent channel flow

Published online by Cambridge University Press:  17 September 2015

A. Scagliarini ,
H. Einarsson ,
Á. Gylfason  and
F. Toschi
A. Scagliarini*
Affiliation:
Department of Physics and INFN, University of Rome ‘Tor Vergata’, Via della Ricerca Scientifica 1, 00133 Rome, Italy School of Science and Engineering, Reykjavik University, Menntavegur 1, IS-101 Reykjavik, Iceland Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands
H. Einarsson
Affiliation:
School of Science and Engineering, Reykjavik University, Menntavegur 1, IS-101 Reykjavik, Iceland
Á. Gylfason
Affiliation:
School of Science and Engineering, Reykjavik University, Menntavegur 1, IS-101 Reykjavik, Iceland
F. Toschi
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands Department of Applied Physics, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands IAC-CNR, Via dei Taurini 19, 00185 Rome, Italy
*
†Email address for correspondence: ascagliarini@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

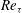We perform direct numerical simulations of an unstably stratified turbulent channel flow to address the effects of buoyancy on the boundary layer dynamics and mean field quantities. We systematically span a range of parameters in the space of friction Reynolds number ($\mathit{Re}_{{\it\tau}}$) and Rayleigh number (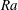$\mathit{Ra}$). Our focus is on deviations from the logarithmic law of the wall due to buoyant motion. The effects of convection in the relevant ranges are discussed, providing measurements of mean profiles of velocity, temperature and Reynolds stresses as well as of the friction coefficient. A phenomenological model is proposed and shown to capture the observed deviations of the velocity profile in the log-law region from the non-convective case.

JFM classification

Boundary Layers: Boundary Layers Convection: Buoyant boundary layers Convection: Convection
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , R5
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Aidun, C. K. & Clausen, J. R. 2010 Lattice Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42, 439–472.Google Scholar
Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.CrossRefGoogle Scholar
Benzi, R., Succi, S. & Vergassola, M. 1992 The lattice Boltzmann equation: theory and applications. Phys. Rep. 222, 145–197.CrossRefGoogle Scholar
Benzi, R., Toschi, F. & Tripiccione, R. 1998 On the heat transfer in Rayleigh–Bénard systems. J. Stat. Phys. 93, 901–918.Google Scholar
Biferale, L., Lohse, D., Mazzitelli, I. & Toschi, F. 2002 Probing structures in channel flow through SO(3) and SO(2) decomposition. J. Fluid Mech. 452, 39–59.Google Scholar
Bluestein, H. B. 2013 Severe Convective Storms and Tornadoes. Springer.Google Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28, 181–189.Google Scholar
Calzavarini, E., Toschi, F. & Tripiccione, R. 2002 Evidences of Bolgiano–Obhukhov scaling in three-dimensional Rayleigh–Bénard convection. Phys. Rev. E 66, 016304.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Deardroff, J. W. 1972 Numerical investigation of neutral and unstable planetary boundary layers. J. Atmos. Sci. 29, 91–115.Google Scholar
Deardroff, J. W. 1974 Three dimensional numerical study of turbulence in an entraining mixed layer. Boundary-Layer Meteorol. 7, 199–226.Google Scholar
Dubrulle, B., Laval, J.-P., Sullivan, P. P. & Werne, J. 2002a A new dynamical subgrid model for the planetary surface layer. Part I: the model and a priori tests. J. Atmos. Sci. 59, 861–876.2.0.CO;2>CrossRefGoogle Scholar
Dubrulle, B., Laval, J.-P., Sullivan, P. P. & Werne, J. 2002b A new dynamical subgrid model for the planetary surface layer. Part II: analytical computation of fluxes, mean profiles, and variances. J. Atmos. Sci. 59, 877–891.Google Scholar
Dyer, A. J. 1974 A review of flux-profile relationships. Boundary-Layer Meteorol. 7, 363–372.Google Scholar
García-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23, 045104.Google Scholar
Gerz, T., Schumann, U. & Elgobashi, S. E. 1989 Direct numerical simulation of stratified homogeneous turbulent shear flows. J. Fluid Mech. 200, 563–594.Google Scholar
Grossmann, S. & Lohse, D. 2011 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Hattori, H., Morita, A. & Nagano, Y. 2006 Nonlinear eddy diffusivity models reflecting buoyancy effect for wall-shear flows and heat transfer. Intl J. Heat Mass Transfer 27, 671–683.Google Scholar
He, X., Chen, S. & Doolen, G. D. 1998 A novel thermal model for the lattice Boltzmann method in incompressible limit. J. Comput. Phys. 146, 282–300.CrossRefGoogle Scholar
Hunt, J. C. R., Kaimal, J. C. & Gaynor, J. E. 1988 Eddy structure in the convective boundary layer-new measurements and new concepts. Q. J. R. Meteorol. Soc. 114, 827–858.Google Scholar
Iida, O. & Kasagi, N. 1997 Direct numerical simulation of unstably stratified turbulent channel flow. Trans. ASME: J. Heat Transfer 119, 53–61.Google Scholar
Iida, O., Kasagi, N. & Nagano, Y. 2002 Direct numerical simulation of turbulent channel flow under stable density stratification. Intl J. Heat Mass Transfer 45, 1693–1703.Google Scholar
Johansson, A. V. & Wikström, P. M. 1999 DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust. 63, 223–245.Google Scholar
Kader, B. A. & Yaglom, A. M. 1990 Mean fields and fluctuations moments in unstably stratified turbulent boundary layers. J. Fluid Mech. 212, 637–662.Google Scholar
Kaimal, J. C., Eversole, R. A., Lenschow, D. H., Stankov, B. B., Kahn, P. H. & Businger, J. A. 1982 Spectral characteristics of the convective boundary layer over uneven terrain. J. Atmos. Sci. 39, 1098–1114.Google Scholar
Komori, S., Ueda, H., Ogino, F. & Mizushina, T. 1982 Turbulence structure in unstably-stratified open-channel flow. Phys. Fluids 25, 1539–1546.CrossRefGoogle Scholar
Lavezzo, V., Clercx, H. J. H. & Toschi, F. 2011 Rayleigh–Bénard convection via Lattice Boltzmann method: code validation and grid resolution effects. J. Phys.: Conf. Ser. 333, 012011.Google Scholar
Lenschow, D. J. 1970 Airplane measurements of planetary boundary layer structure. J. Appl. Meteorol. 9, 874–884.Google Scholar
L’vov, V. S., Pomyalov, A., Procaccia, I. & Tiberkevich, V. 2004 Drag reduction by polymers in wall bounded turbulence. Phys. Rev. Lett. 92, 244503.Google Scholar
Lumley, J. L., Zeman, O. & Siess, J. 1978 The influence of buoyancy on turbulent transport. J. Fluid Mech. 84, 581–597.Google Scholar
Mellor, G. L. & Yamada, T. 1974 A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 41, 1791–1806.Google Scholar
Mellor, G. L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 20, 851–875.Google Scholar
Moeng, C.-H. 1984 A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.2.0.CO;2>CrossRefGoogle Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the atmospheric boundary layer. Trudy Inst. Teor. Geofiz. Akad. Nauk SSSR 24, 163–187.Google Scholar
Obukhov, A. M. 1946 Turbulence in thermally inhomogeneous atmosphere. Trudy Inst. Teor. Geofiz. Akad. Nauk SSSR 1, 95–115.Google Scholar
Papavassiliou, D. V. & Hanratty, T. J. 1997 Transport of a passive scalar in a turbulent channel flow. Intl J. Heat Mass Transfer 40, 1303–1311.Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. 1932 Meteorologische Anwendung der Strömungslehre. Beitr. Phys. Atmos. 19, 188–202.Google Scholar
Scagliarini, A., Gylfason, A. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89, 043012.Google Scholar
Toschi, F., Amati, G., Succi, S., Benzi, R. & Piva, R. 1999 Intermittency and structure functions in channel flow turbulence. Phys. Rev. Lett. 82, 5044–5047.Google Scholar
Toschi, F., Lévêque, E. & Ruiz-Chavarría, G. 2000 Shear effects in nonhomogeneous turbulence. Phys. Rev. Lett. 85, 1436–1439.Google Scholar
Zainali, A. & Lessani, B. 2010 Large-eddy simulations of unstably stratified turbulent channel flow with high temperature differences. Intl J. Heat Mass Transfer 53, 4865–4875.Google Scholar
Zonta, F., Onorato, M. & Soldati, A. 2012 Turbulence and internal waves in stably-stratified channel flow with temperature-dependent fluid properties. J. Fluid Mech. 697, 175–203.Google Scholar