Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T21:31:40.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Gyrotaxis in uniform vorticity

Published online by Cambridge University Press:  04 December 2014

T. J. Pedley
T. J. Pedley*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: t.j.pedley@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Analysis of bioconvection in dilute suspensions of bottom-heavy but randomly swimming micro-organisms is commonly based on a model introduced in 1990. This couples the Navier–Stokes equations, the cell conservation equation and the Fokker–Planck equation (FPE) for the probability density function for a cell’s swimming direction 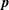$\boldsymbol{p}$, which balances rotational diffusion against viscous and gravitational torques. The results have shown qualitative agreement with observation, but the model has not been subjected to direct quantitative testing in a controlled experiment. Here, we consider a simple configuration in which the suspension is contained in a circular cylinder of radius 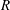$R$, which rotates at angular velocity ${\rm\Omega}$ about a horizontal axis. We solve the FPE and calculate the cells’ mean swimming velocity, which proves to be horizontal when 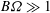$B{\rm\Omega}\gg 1$, where $B$ is the gyrotactic reorientation time scale. Then we compute the cell concentration distribution, which is non-uniform only in a thin boundary layer near the cylinder wall when 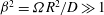${\it\beta}^{2}={\rm\Omega}R^{2}/D\gg 1$, where 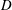$D$ is the cells’ translational diffusivity. The fact that cells are denser than water means that this concentration distribution drives a perturbation to the underlying solid-body rotational flow which can be calculated analytically. The predictions of the theory are evaluated in terms of a proposed experimental realisation of the configuration, using suspensions of the alga Chlamydomonas nivalis or Chlamydomonas reinhardtii or the algal colony Volvox.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Micro-organism dynamics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , R6
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bees, M. A. & Hill, N. A. 1997 Wavelengths of bioconvection patterns. J. Expl Biol. 200, 1515–1526.CrossRefGoogle ScholarPubMed
Bees, M. A. & Hill, N. A. 1999 Non-linear bioconvection in a deep suspension of gyrotactic swimming micro-organisms. J. Math. Biol. 38, 135–168.CrossRefGoogle Scholar
Bees, M. A., Hill, N. A. & Pedley, T. J. 1998 Analytical approximations for the orientation distribution of small dipolar particles in steady shear flows. J. Math. Biol. 36, 269–298.CrossRefGoogle Scholar
Carslaw, H. S. & Jaeger, J. C. 1959 Conduction of Heat in Solids, 2nd edn. Clarendon.Google Scholar
Childress, S., Levandowsky, M. & Spiegel, E. A. 1975 Pattern formation in a suspension of swimming micro-organisms. J. Fluid Mech. 69, 591–613.CrossRefGoogle Scholar
Cisneros, L. H., Cortez, R., Dombrowski, C., Goldstein, R. E. & Kessler, J. O. 2007 Fluid dynamics of self-propelled micro-organisms, from individuals to concentrated populations. Exp. Fluids 43, 737–753.CrossRefGoogle Scholar
Drescher, K., Leptos, K., Tuval, I., Ishikawa, T., Pedley, T. J. & Goldstein, R. E. 2009 Dancing Volvox: hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102, 168101.CrossRefGoogle ScholarPubMed
Ezhilan, B., Shelley, M. J. & Saintillan, D. 2013 Instabilities and nonlinear dynamics of concentrated active suspensions. Phys. Fluids 25, 070697.CrossRefGoogle Scholar
Ghorai, S. & Hill, N. A. 1999 Development and stability of gyrotactic plumes in bioconvection. J. Fluid Mech. 400, 1–31.CrossRefGoogle Scholar
Hill, N. A. & Häder, D. P. 1997 A biased random walk model for the trajectories of swimming micro-organisms. J. Theor. Biol. 186, 503–526.CrossRefGoogle ScholarPubMed
Hill, N. A. & Pedley, T. J. 2005 Bioconvection. Fluid Dyn. Res. 37, 1–20.CrossRefGoogle Scholar
Hill, N. A., Pedley, T. J. & Kessler, J. O. 1989 Growth of bioconvection patterns in a suspension of gyrotactic micro-organisms in a layer of finite depth. J. Fluid Mech. 208, 509–543.CrossRefGoogle Scholar
Hwang, Y. & Pedley, T. J. 2014 Bioconvection under uniform shear: linear stability analysis. J. Fluid Mech. 738, 522–562.CrossRefGoogle Scholar
Kantsler, V., Dunkel, J., Polin, M. & Goldstein, R. E. 2013 Ciliary contact interactions dominate surface scattering of swimming eukaryotes. Proc. Natl Acad. Sci. USA 110, 1187–1192.CrossRefGoogle ScholarPubMed
Kessler, J. O. 1985 Co-operative and concentrative phenomena of swimming microorganisms. Contemp. Phys. 26, 147–166.CrossRefGoogle Scholar
Kessler, J. O. 1986 Individual and collective dynamics of swimming cells. J. Fluid Mech. 173, 191–205.CrossRefGoogle Scholar
Kessler, J. O., Hill, N. A., Strittmatter, R. & Wiseley, D. 1998 Sedimenting particles and swimming micro-organisms in a rotating fluid. Adv. Space Res. 21, 1269–1275.Google Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming micro-organisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.CrossRefGoogle Scholar
Pedley, T. J. 2010 Instability of uniform microorganism suspensions revisited. J. Fluid Mech. 647, 335–359.CrossRefGoogle Scholar
Pedley, T. J., Hill, N. A. & Kessler, J. O. 1988 The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 195, 223–237.CrossRefGoogle Scholar
Pedley, T. J. & Kessler, J. O. 1990 A new continuum model for suspensions of gyrotactic micro-organisms. J. Fluid Mech. 212, 155–182.CrossRefGoogle ScholarPubMed
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming micro-organisms. Annu. Rev. Fluid Mech. 24, 313–358.CrossRefGoogle Scholar
Platt, J. R. 1961 Bioconvection patterns in cultures of free-swimming organisms. Science 133, 1766–1767.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008 Instabilities, pattern formation, and mixing in active particle suspensions. Phys. Fluids 20, 123304.CrossRefGoogle Scholar
Saintillan, D. & Shelley, M. J. 2012 Emergence of coherent structures and large-scale flows in motile suspensions. J. R. Soc. Interface 9, 571–585.CrossRefGoogle ScholarPubMed
Simha, R. A. & Ramaswamy, S. 2002 Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89, 058101.Google Scholar
Thorn, G. J. & Bearon, R. N. 2010 Transport of spherical gyrotactic organisms in general three-dimensional flow fields. Phys. Fluids 22, 041902.CrossRefGoogle Scholar