Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-20T04:28:58.859Z Has data issue: false hasContentIssue false
  • English
  • Français

Gravity current propagation up a valley

Published online by Cambridge University Press:  04 December 2014

Catherine S. Jones ,
Claudia Cenedese ,
Eric P. Chassignet ,
P. F. Linden  and
Bruce R. Sutherland
Catherine S. Jones*
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
Claudia Cenedese
Affiliation:
Woods Hole Oceanographic Institution, 266 Woods Hole Road, Woods Hole, MA 02543-1050, USA
Eric P. Chassignet
Affiliation:
Center for Ocean–Atmospheric Prediction Studies (COAPS), Florida State University, 2000 Levy Avenue, Building A, Suite 292, Tallahassee, FL 32306-2741, USA
P. F. Linden
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Bruce R. Sutherland
Affiliation:
Department of Physics, and Department of Earth & Atmospheric Sciences, University of Alberta, Edmonton, AB, T6G 2E1, Canada
*
†Email address for correspondence: csjones@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The advance of the front of a dense gravity current propagating in a rectangular channel and V-shaped valley both horizontally and up a shallow slope is examined through theory, full-depth lock–release laboratory experiments and hydrostatic numerical simulations. Consistent with theory, experiments and simulations show that the front speed is relatively faster in the valley than in the channel. The front speed measured shortly after release from the lock is 5–22 % smaller than theory, with greater discrepancy found in upsloping V-shaped valleys. 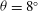By contrast, the simulated speed is approximately 6 % larger than theory, showing no dependence on slope for rise angles up to ${\it\theta}=8^{\circ }$. Unlike gravity currents in a channel, the current head is observed in experiments to be more turbulent when propagating in a V-shaped valley. The turbulence is presumably enhanced due to the lateral flows down the sloping sides of the valley. As a consequence, lateral momentum transport contributes to the observed lower initial speeds. A Wentzel–Kramers–Brillouin like theory predicting the deceleration of the current as it runs upslope agrees remarkably well with simulations and with most experiments, within errors.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 417 - 434
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Birman, V. K., Battandier, B. A., Meiburg, E. & Linden, P. F. 2007 Lock-exchange flows in sloping channels. J. Fluid Mech. 577, 53–77.CrossRefGoogle Scholar
Bleck, R. 2002 An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Model. 4, 55–88.CrossRefGoogle Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99, 531–543.Google Scholar
Chassignet, E. P., Smith, L. T., Halliwell, G. R. & Bleck, R. 2003 North Atlantic simulations with the hybrid coordinate ocean model (HYCOM): impact of the vertical coordinate choice, reference pressure, and thermobaricity. J. Phys. Oceanogr. 33, 2504–2526.Google Scholar
Cuthbertson, A. J. S., Lundberg, P., Davies, P. A. & Laanearu, J. 2014 Gravity currents in rotating, wedge-shaped, adverse channels. Environ. Fluid Mech. 14, 1251–1273.Google Scholar
Darelius, E. 2008 Topographic steering of dense overflows: laboratory experiments with V-shaped ridges and canyons. Deep-Sea Res. 44, 1021–1034.Google Scholar
Halliwell, G. R. 2004 Evaluation of vertical coordinate and vertical mixing algorithms in the hybrid-coordinate ocean model (HYCOM). Ocean Model. 7, 285–322.Google Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.Google Scholar
Keulegan, G. H.1957 An experimental study of the motion of saline water from locks into fresh water channels. Tech. Rep. 5168. National Bureau of Standards.Google Scholar
Klemp, J. B., Rotunno, R. & Skamarock, W. C. 1994 On the dynamics of gravity currents in a channel. J. Fluid Mech. 269, 169–198.Google Scholar
Lane-Serff, G. F., Beal, L. M. & Hadfield, T. D. 1995 Gravity current flow over obstacles. J. Fluid Mech. 292, 39–53.Google Scholar
Marino, B. M. & Thomas, L. P. 2009 Front condition for gravity currents in channels of nonrectangular symmetric cross-section shapes. Trans. ASME: J. Fluids Engng 131, 051201.Google Scholar
Marleau, L. J., Flynn, M. R. & Sutherland, B. R. 2014 Gravity currents propagating up a slope. Phys. Fluids 26, 046605.Google Scholar
Monaghan, J., Mériaux, C. & Huppert, H. 2009 High Reynolds number gravity currents along V-shaped valleys. Eur. J. Mech. (B/Fluids) 28, 651–659.Google Scholar
Ottolenghi, L., Adduce, C., Inghilesi, R., Roman, F. & Armenio, V. 2015 Mixing in gravity currents propagating up a slope: large eddy simulations and laboratory experiments. J. Fluid Mech. (submitted).Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.Google Scholar
Rottman, J. W., Simpson, J. E., Hunt, J. C. R. & Britter, R. E. 1985 Unsteady gravity current flows over obstacles: some observations and analysis related to the phase II trials. J. Hazard. Mater. 11, 325–340.Google Scholar
Safrai, A. & Tkachenko, I. 2009 Numerical modeling of gravity currents in inclined channels. Fluid Dyn. 44, 22–30.Google Scholar
Shin, J., Dalziel, S. & Linden, P. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.CrossRefGoogle Scholar
Simpson, J. E. 1982 Gravity currents in the laboratory, atmosphere, and ocean. Annu. Rev. Fluid Mech. 14, 213–234.Google Scholar
Simpson, J. E. 1997 Gravity Currents, 2nd edn. Cambridge University Press.Google Scholar
Sutherland, B. R., Polet, D. & Campbell, M. 2013 Gravity currents shoaling on a slope. Phys. Fluids 25, 086604.Google Scholar
Takagi, D. & Huppert, H. 2007 The effect of confining boundaries on viscous gravity currents. J. Fluid Mech. 577, 495–505.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman and Hall/CRC Press.Google Scholar
Ungarish, M. 2013 Two-layer shallow-water dam-break solutions for gravity currents in non-rectangular cross-area channels. J. Fluid Mech. 732, 232–249.Google Scholar
Ungarish, M., Mériaux, C. A. & Kurz-Besson, C. B. 2014 The propagation of gravity currents in a V-shaped triangular cross-section channel: experiments and theory. J. Fluid Mech. 754, 537–570.Google Scholar
Zemach, T. & Ungarish, M. 2013 Gravity currents in non-rectangular cross-section channels: analytical and numerical solutions of the one-layer shallow-water model for high-Reynolds-number propagation. Phys. Fluids 25, 026601.Google Scholar