Article contents
Convective shutdown in a porous medium at high Rayleigh number
Published online by Cambridge University Press: 19 February 2013
Abstract
Convection in a closed domain driven by a dense buoyancy source along the upper boundary soon starts to wane owing to the increase of the average interior density. In this paper, theoretical and numerical models are developed of the subsequent long period of shutdown of convection in a two-dimensional porous medium at high Rayleigh number 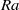 $\mathit{Ra}$. The aims of this paper are twofold. Firstly, the relationship between this slowly evolving ‘one-sided’ shutdown system and the statistically steady ‘two-sided’ Rayleigh–Bénard (RB) cell is investigated. Numerical measurements of the Nusselt number
$\mathit{Ra}$. The aims of this paper are twofold. Firstly, the relationship between this slowly evolving ‘one-sided’ shutdown system and the statistically steady ‘two-sided’ Rayleigh–Bénard (RB) cell is investigated. Numerical measurements of the Nusselt number 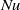 $\mathit{Nu}$ from an RB cell (Hewitt et al., Phys. Rev. Lett., vol. 108, 2012, 224503) are very well described by the simple parametrization
$\mathit{Nu}$ from an RB cell (Hewitt et al., Phys. Rev. Lett., vol. 108, 2012, 224503) are very well described by the simple parametrization 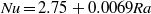 $\mathit{Nu}= 2. 75+ 0. 0069\mathit{Ra}$. This parametrization is used in theoretical box models of the one-sided shutdown system and found to give excellent agreement with high-resolution numerical simulations of this system. The dynamical structure of shutdown can also be accurately predicted by measurements from an RB cell. Results are presented for a general power-law equation of state. Secondly, these ideas are extended to model more complex physical systems, which comprise two fluid layers with an equation of state such that the solution that forms at the (moving) interface is more dense than either layer. The two fluids are either immiscible or miscible. Theoretical box models compare well with numerical simulations in the case of a flat interface between the fluids. Experimental results from a Hele-Shaw cell and numerical simulations both show that interfacial deformation can dramatically enhance the convective flux. The applicability of these results to the convective dissolution of geologically sequestered
$\mathit{Nu}= 2. 75+ 0. 0069\mathit{Ra}$. This parametrization is used in theoretical box models of the one-sided shutdown system and found to give excellent agreement with high-resolution numerical simulations of this system. The dynamical structure of shutdown can also be accurately predicted by measurements from an RB cell. Results are presented for a general power-law equation of state. Secondly, these ideas are extended to model more complex physical systems, which comprise two fluid layers with an equation of state such that the solution that forms at the (moving) interface is more dense than either layer. The two fluids are either immiscible or miscible. Theoretical box models compare well with numerical simulations in the case of a flat interface between the fluids. Experimental results from a Hele-Shaw cell and numerical simulations both show that interfacial deformation can dramatically enhance the convective flux. The applicability of these results to the convective dissolution of geologically sequestered 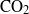 ${\mathrm{CO} }_{2} $ in a saline aquifer is discussed.
${\mathrm{CO} }_{2} $ in a saline aquifer is discussed.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 102
- Cited by


