Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T18:12:47.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Consequences of viscous anisotropy in a deforming, two-phase aggregate. Why is porosity-band angle lowered by viscous anisotropy?

Published online by Cambridge University Press:  03 November 2015

Yasuko Takei  and
Richard F. Katz Open the ORCID record for Richard F. Katz [Opens in a new window]
Yasuko Takei*
Affiliation:
Earthquake Research Institute, University of Tokyo, Tokyo 113-0032, Japan
Richard F. Katz
Affiliation:
Department of Earth Sciences, University of Oxford, South Parks Road, Oxford OX1 3AN, UK
*
†Email address for correspondence: ytakei@eri.u-tokyo.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

In laboratory experiments that impose shear deformation on partially molten aggregates of initially uniform porosity, melt segregates into high-porosity sheets (bands in cross-section). The bands emerge at 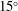$15^{\circ }$–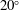$20^{\circ }$ to the shear plane. A model of viscous anisotropy can explain these low angles whereas previous simpler models have failed to do so. The anisotropic model is complex, however, and the reason that it produces low-angle bands has not been understood. Here we show that there are two mechanisms: (i) suppression of the well-known tensile instability, and (ii) creation of a new shear-driven instability. We elucidate these mechanisms using linearised stability analysis in a coordinate system that is aligned with the perturbations. We consider the general case of anisotropy that varies dynamically with deviatoric stress, but approach it by first considering uniform anisotropy that is imposed a priori and showing the difference between static and dynamic cases. We extend the model of viscous anisotropy to include a strengthening in the direction of maximum compressive stress. Our results support the hypothesis that viscous anisotropy is the cause of low band angles in experiments.

JFM classification

Geophysical and Geological Flows: Magma and lava flow Non-Newtonian Flows: Non-Newtonian Flows Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 199 - 224
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allwright, J. & Katz, R. F. 2014 Pipe Poiseuille flow of viscously anisotropic, partially molten rock. Geophys. J. Intl 199 (3), 1608–1624.CrossRefGoogle Scholar
Balay, S., Buschelman, K., Gropp, W. D., Kaushik, D., Knepley, M., McInnes, L. C., Smith, B. F. & Zhang, H.2001 PETSc, http://www.mcs.anl.gov/petsc.Google Scholar
Balay, S., Buschelman, K., Gropp, W. D., Kaushik, D., Knepley, M., McInnes, L. C., Smith, B. F. & Zhang, H.2004 PETSc users’ manual. Tech. Rep. Argonne National Laboratory.Google Scholar
Butler, S. L. 2012 Numerical models of shear-induced melt band formation with anisotropic matrix viscosity. Phys. Earth Planet. Inter. 200–201, 28–36.Google Scholar
Cooper, R. F., Kohlstedt, D. L. & Chyung, K. 1989 Solution–precipitation enhanced creep in solid–liquid aggregates which display a non-zero dihedral angle. Acta Metall. 37, 1759–1771.CrossRefGoogle Scholar
Daines, M. J. & Kohlstedt, D. L. 1997 Influence of deformation on melt topology in peridotites. J. Geophys. Res. 102, 10257–10271.Google Scholar
Drew, D. A. 1983 Mathematical modeling of two-phase flow. Annu. Rev. Fluid Mech. 15, 261–291.Google Scholar
Holtzman, B. K., Groebner, N. J., Zimmerman, M. E., Ginsberg, S. B. & Kohlstedt, D. L. 2003 Stress-driven melt segregation in partially molten rocks. Geochem. Geophys. Geosyst. 4 (5), 8607.Google Scholar
Holtzman, B. K. & Kohlstedt, D. L. 2007 Stress-driven melt segregation and strain partitioning in partially molten rocks: effects of stress and strain. J. Petrol. 48, 2379–2406.Google Scholar
Karato, S. & Wu, P. 1993 Rheology of the upper mantle – a synthesis. Science 260 (5109), 771–778.Google Scholar
Katz, R. F., Knepley, M. G., Smith, B., Spiegelman, M. & Coon, E. T. 2007 Numerical simulation of geodynamic processes with the Portable Extensible Toolkit for Scientific Computation. Phys. Earth Planet. Inter. 163, 52–68.Google Scholar
Katz, R. F., Spiegelman, M. & Holtzman, B. 2006 The dynamics of melt and shear localization in partially molten aggregates. Nature 442 (7103), 676–679.CrossRefGoogle ScholarPubMed
Katz, R. F. & Takei, Y. 2013 Consequences of viscous anisotropy in a deforming, two-phase aggregate: 2. Numerical solutions of the full equations. J. Fluid Mech. 734, 456–485.Google Scholar
King, D. S. H., Holtzman, B. K. & Kohlstedt, D. L. 2011 An experimental investigation of the interactions between reaction-driven and stress-driven melt segregation: 1. Application to mantle melt extraction. Geochem. Geophys. Geosyst. 12 (12), 12019.Google Scholar
King, D. S. H., Zimmerman, M. E. & Kohlstedt, D. L. 2010 Stress-driven melt segregation in partially molten olivine-rich rocks deformed in torsion. J. Petrol. 51, 21–42.Google Scholar
McKenzie, D. 1984 The generation and compaction of partially molten rock. J. Petrol. 25 (3), 713–765.Google Scholar
Mei, S., Bai, W., Hiraga, T. & Kohlstedt, D. L. 2002 Influence of melt on the creep behavior of olivine–basalt aggregates under hydrous conditions. Earth Planet. Sci. Lett. 201, 491–507.Google Scholar
Qi, C., Kohlstedt, D., Katz, R. F. & Takei, Y. 2015 An experimental test of the viscous anisotropy hypothesis for partially molten rocks. Proc. Natl Acad. Sci. USA 112 (41), 12616–12620.CrossRefGoogle ScholarPubMed
Rudge, J. F. & Bercovici, D. 2015 Melt-band instabilities with two-phase damage. Geophys. J. Intl 201 (2), 640–651.Google Scholar
Rudge, J. F., Bercovici, D. & Spiegelman, M. 2011 Disequilibrium melting of a two phase multicomponent mantle. Geophys. J. Intl 184 (2), 699–718.Google Scholar
Simpson, G., Spiegelman, M. & Weinstein, M. I. 2010a A multiscale model of partial melts: 1. Effective equations. J. Geophys. Res. 115, B04410.Google Scholar
Simpson, G., Spiegelman, M. & Weinstein, M. I. 2010b A multiscale model of partial melts: 2. Numerical results. J. Geophys. Res. 115, B04411.Google Scholar
Spiegelman, M. 2003 Linear analysis of melt band formation by simple shear. Geochem. Geophys. Geosyst 4 (9), 8615.Google Scholar
Stevenson, D. J. 1989 Spontaneous small-scale melt segregation in partial melts undergoing deformation. Geophys. Res. Lett. 16 (9), 1067–1070.Google Scholar
Takei, Y. 1998 Constitutive mechanical relations of solid–liquid composites in terms of grain-boundary contiguity. J. Geophys. Res. 103, 18183–18203.CrossRefGoogle Scholar
Takei, Y. 2010 Stress-induced anisotropy of partially molten rock analogue deformed under quasi-static loading test. J. Geophys. Res. 115, B03204.Google Scholar
Takei, Y. & Holtzman, B. K. 2009 a Viscous constitutive relations of solid–liquid composites in terms of grain boundary contiguity: 1. Grain boundary diffusion control model. J. Geophys. Res. 114, B06205.Google Scholar
Takei, Y. & Holtzman, B. K. 2009b Viscous constitutive relations of solid–liquid composites in terms of grain boundary contiguity: 3. Causes and consequences of viscous anisotropy. J. Geophys. Res 114, B06207.Google Scholar
Takei, Y. & Katz, R. F. 2013 Consequences of viscous anisotropy in a deforming, two-phase aggregate: 1. Governing equations and linearised analysis. J. Fluid Mech. 734, 424–455.CrossRefGoogle Scholar
Zimmerman, M. E., Zhang, S. Q., Kohlstedt, D. L. & Karato, S. 1999 Melt distribution in mantle rocks deformed in shear. Geophys. Res. Lett. 26 (10), 1505–1508.CrossRefGoogle Scholar