Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-27T10:14:04.924Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent structures and dominant frequencies in a turbulent three-dimensional diffuser

Published online by Cambridge University Press:  12 April 2012

Johan Malm ,
Philipp Schlatter  and
Dan S. Henningson
Johan Malm*
Affiliation:
Linné FLOW Centre, Swedish e-Science Research Centre (SeRC) and KTH Mechanics, Osquars Backe 18, SE-100 44 Stockholm, Sweden
Philipp Schlatter
Affiliation:
Linné FLOW Centre, Swedish e-Science Research Centre (SeRC) and KTH Mechanics, Osquars Backe 18, SE-100 44 Stockholm, Sweden
Dan S. Henningson
Affiliation:
Linné FLOW Centre, Swedish e-Science Research Centre (SeRC) and KTH Mechanics, Osquars Backe 18, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: johan@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Dominant frequencies and coherent structures are investigated in a turbulent, three-dimensional and separated diffuser flow at (based on bulk velocity and inflow-duct height), where mean flow characteristics were first studied experimentally by Cherry, Elkins and Eaton (Intl J. Heat Fluid Flow, vol. 29, 2008, pp. 803–811) and later numerically by Ohlsson et al. (J. Fluid Mech., vol. 650, 2010, pp. 307–318). Coherent structures are educed by proper orthogonal decomposition (POD) of the flow, which together with time probes located in the flow domain are used to extract frequency information. The present study shows that the flow contains multiple phenomena, well separated in frequency space. Dominant large-scale frequencies in a narrow band 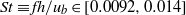(where 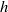is the inflow-duct height and 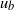is the bulk velocity), yielding time periods 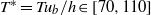, are deduced from the time signal probes in the upper separated part of the diffuser. The associated structures identified by the POD are large streaks arising from a sinusoidal oscillating motion in the diffuser. Their individual contributions to the total kinetic energy, dominated by the mean flow, are, however, small. The reason for the oscillating movement in this low-frequency range is concluded to be the confinement of the flow in this particular geometric set-up in combination with the high Reynolds number and the large separated zone on the top diffuser wall. Based on this analysis, it is shown that the bulk of the streamwise root mean square (r.m.s.) value arises due to large-scale motion, which in turn can explain the appearance of two or more peaks in the streamwise r.m.s. value. The weak secondary flow present in the inflow duct is shown to survive into the diffuser, where it experiences an imbalance with respect to the upper expanding corners, thereby giving rise to the asymmetry of the mean separated region in the diffuser.

JFM classification

Wakes/Jets: Jets Wakes/Jets: Separated flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 699 , 25 May 2012 , pp. 320 - 351
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adams, N. A. 2000 Direct simulation of the turbulent boundary layer along a compression ramp at and . J. Fluid Mech. 420, 47–83.CrossRefGoogle Scholar
2. Cazemier, W., Verstappen, R. W. C. P. & Veldman, A. E. P. 1998 Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys. Fluids 10 (7), 1685–1699.CrossRefGoogle Scholar
3. Cherry, E. M., Elkins, C. J. & Eaton, J. K. 2008 Geometric sensitivity of three-dimensional separated flows. Intl J. Heat Fluid Flow 29 (3), 803–811.CrossRefGoogle Scholar
4. Cherry, E. M., Elkins, C. J. & Eaton, J. K. 2009 Pressure measurements in a three-dimensional separated diffuser. Intl J. Heat Fluid Flow 30 (1), 1–2.CrossRefGoogle Scholar
5. Délery, J. M. 2001 Robert Legendre and Henri Werlé: toward the elucidation of three-dimensional separation. Annu. Rev. Fluid Mech. 33 (1), 129–154.CrossRefGoogle Scholar
6. Eaton, J. K. & Johnston, J. P. 1980 Turbulent flow reattachment – an experimental study of the flow and structure behind a backward-facing step. Tech. Rep. MD-39. Thermosciences Division, Stanford University.Google Scholar
7. Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133 (1), 84–101.CrossRefGoogle Scholar
8. Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G. 2008 nek5000 web page. http://nek5000.mcs.anl.gov.Google Scholar
9. Friedrich, R. & Arnal, M. 1990 Analysing turbulent backward-facing step flow with the lowpass-filtered Navier–Stokes equations. J. Wind Engng. Ind. Aerodyn. 35, 101–128.CrossRefGoogle Scholar
10. Herbst, A. H., Schlatter, P. & Henningson, D. S. 2007 Simulations of turbulent flow in a plane asymmetric diffuser. Flow Turbul. Combust. 79, 275–306.CrossRefGoogle Scholar
11. Holmes, P., Lumley, J. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
12. Jakirlić, S., Kadavelil, G., Kornhaas, M., Schäfer, M., Sternel, D. C. & Tropea, C. 2010a Numerical and physical aspects in LES and hybrid LES/RANS of turbulent flow separation in a 3-D diffuser. Intl J. Heat Fluid Flow 31 (5), 820–832.CrossRefGoogle Scholar
13. Jakirlić, S., Kadavelil, G., Sirbubalo, E., Breuer, M., von Terzi, D. & Borello, D. 2010 b In 14th ERCOFTAC SIG15 Workshop on Refined Turbulence Modelling: Turbulent Flow Separation in a 3-D Diffuser. ERCOFTAC Bulletin, December, Issue 85, case 13.2 (1). ERCOFTAC.Google Scholar
14. Kaltenbach, H.-J., Fatica, M., Mittal, R., Lund, T. S. & Moin, P. 1999 Study of flow in a planar asymmetric diffuser using large-eddy simulation. J. Fluid Mech. 390, 151–185.CrossRefGoogle Scholar
15. Kiya, M. & Sasaki, K. 1985 Structure of large-scale vortices and unsteady reverse flow in the reattaching zone of a turbulent separation bubble. J. Fluid Mech. 154, 463–491.CrossRefGoogle Scholar
16. Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flow. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
17. Lawson, N. J. & Davidson, M. R. 2001 Self-sustained oscillation of a submerged jet in a thin rectangular cavity. J. Fluids Struct. 15 (1), 59–81.CrossRefGoogle Scholar
18. Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.CrossRefGoogle Scholar
19. Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I. ), pp. 166–178. Nauka, Moscow.Google Scholar
20. Lygren, M. & Andersson, H. 1999 Influence of boundary conditions on the large scale structures in turbulent plane Couette flow. In Turbulence and Shear Flow Phenomena 1 (ed. Banerjee, S. & Eaton, J. ), pp. 15–20. Begell House.CrossRefGoogle Scholar
21. Manhart, M. & Wengle, H. 1993 A spatiotemporal decomposition of a fully inhomogeneous turbulent flow field. Theor. Comput. Fluid Dyn. 5, 223–242.CrossRefGoogle Scholar
22. Maurel, A., Ern, P., Zielinska, B. J. A. & Wesfreid, J. E. 1996 Experimental study of self-sustained oscillations in a confined jet. Phys. Rev. E 54 (4), 3643–3651.CrossRefGoogle Scholar
23. Moin, P. & Moser, R. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.CrossRefGoogle Scholar
24. Moreno, D., Krothapalli, A., Alkislar, M. B. & Lourenco, L. M. 2004 Low-dimensional model of a supersonic rectangular jet. Phys. Rev. E 69 (2), 026304.CrossRefGoogle ScholarPubMed
25. Na, Y. & Moin, P. 1998 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.CrossRefGoogle Scholar
26. Ohlsson, J., Schlatter, P., Fischer, P. F. & Henningson, D. S. 2010 Direct numerical simulation of separated flow in a three-dimensional diffuser. J. Fluid Mech. 650, 307–318 (note change of name from J. Ohlsson to J. Malm).CrossRefGoogle Scholar
27. Piquet, J. 1999 Turbulent Flows: Models and Physics. Springer.CrossRefGoogle Scholar
28. Rowley, C. W., Mezić, I, Bagheri, S, Schlatter, P & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
29. Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H. M., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to studied through numerical simulation and experiments. Phys. Fluids 21 (5), 051702.CrossRefGoogle Scholar
30. Schneider, H., von Terzi, D. A., Bauer, H. J. & Rodi, W. 2010 Reliable and accurate prediction of three-dimensional separation in asymmetric diffusers using large-eddy simulation. J. Fluids Engng 132, 031101.CrossRefGoogle Scholar
31. Simpson, R. L. 1981 A review of some phenomena in turbulent flow separation. Trans. ASME: J. Fluids Engng 102, 520–533.Google Scholar
32. Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21 (1), 205–232.CrossRefGoogle Scholar
33. Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Parts I–III. Q. Appl. Maths 45, 561–590.CrossRefGoogle Scholar
34. Spille-Kohoff, A. & Kaltenbach, H.-J. 2001 Generation of turbulent inflow data with a prescribed shear-stress profile. In DNS/LES Progress and Challenges, Third AFSOR Conference on DNS and LES, Arlington, Texas (ed. Liu, C., Sakell, L. & Beutner, T. ). Greyden Press.Google Scholar
35. Törnblom, O., Lindgren, B. & Johansson, A. V. 2009 The separating flow in a plane asymmetric diffuser with opening angle: mean flow and turbulence statistics, temporal behaviour and flow structures. J. Fluid Mech. 636, 337–370.CrossRefGoogle Scholar
36. Tufo, H. M. & Fischer, P. F. 2001 Fast parallel direct solvers for coarse grid problems. J. Parallel Distrib. Comput. 61 (2), 151–177.CrossRefGoogle Scholar
37. Villermaux, E. & Hopfinger, E. J. 1994 Self-sustained oscillations of a confined jet: a case study for the nonlinear delayed saturation model. Physica D 72 (3), 230–243.CrossRefGoogle Scholar
38. Wang, C., Jang, Y. J. & Leschziner, M. A. 2004 Modelling two- and three-dimensional separation from curved surfaces with anisotropy-resolving turbulence closures. Intl J. Heat Fluid Flow 25 (3), 499–512.CrossRefGoogle Scholar