Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T15:17:16.962Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall-separation and vortex-breakdown zones in a solid-body rotation flow in a rotating finite-length straight circular pipe

Published online by Cambridge University Press:  24 October 2014

Zvi Rusak  and
Shixiao Wang
Zvi Rusak*
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Shixiao Wang
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland, 1142, New Zealand
*
†Email address for correspondence: rusakz@rpi.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The incompressible, inviscid and axisymmetric dynamics of perturbations on a solid-body rotation flow with a uniform axial velocity in a rotating, finite-length, straight, circular pipe are studied via global analysis techniques and numerical simulations. The investigation establishes the coexistence of both axisymmetric wall-separation and vortex-breakdown zones above a critical swirl level, 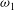${\it\omega}_{1}$. We first describe the bifurcation diagram of steady-state solutions of the flow problem as a function of the swirl ratio 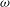${\it\omega}$. We prove that the base columnar flow is a unique steady-state solution when 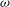${\it\omega}$ is below 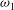${\it\omega}_{1}$. This state is asymptotically stable and a global attractor of the flow dynamics. However, when 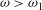${\it\omega}>{\it\omega}_{1}$, we reveal, in addition to the base columnar flow, the coexistence of states that describe swirling flows around either centreline stagnant breakdown zones or wall quasi-stagnant zones, where both the axial and radial velocities vanish. We demonstrate that when 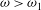${\it\omega}>{\it\omega}_{1}$, the base columnar flow is a min–max point of an energy functional that governs the problem, while the swirling flows around the quasi-stagnant and stagnant zones are global and local minimizer states and become attractors of the flow dynamics. We also find additional min–max states that are transient attractors of the flow dynamics. Numerical simulations describe the evolution of perturbations on above-critical columnar states to either the breakdown or the wall-separation states. The growth of perturbations in both cases is composed of a linear stage of the evolution, with growth rates accurately predicted by the analysis of Wang & Rusak (Phys. Fluids, vol. 8, 1996a, pp. 1007–1016), followed by a stage of saturation to either one of the separation zone states. The wall-separation states have the same chance of appearing as that of vortex-breakdown states and there is no hysteresis loop between them. This is strikingly different from the dynamics of vortices with medium or narrow vortical core size in a pipe.

JFM classification

Vortex Flows: Vortex breakdown Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 321 - 359
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.CrossRefGoogle Scholar
Benjamin, T. B. 1967 Some developments in the theory of vortex breakdown. J. Fluid Mech. 28 (1), 65–84.CrossRefGoogle Scholar
Beran, P. S. 1994 The time-asymptotic behavior of vortex breakdown in tubes. Comput. Fluids 23, 913–937.Google Scholar
Beran, P. S. & Culick, F. E. C. 1992 The role of non-uniqueness in the development of vortex breakdown in tubes. J. Fluid Mech. 242, 491–527.Google Scholar
Bragg, S. L. & Hawthorne, W. R. 1950 Some exact solutions of the flow through annular cascade actuator discs. J. Aero. Sci. 17, 243–249.CrossRefGoogle Scholar
Brucker, Ch. & Althaus, W. 1995 Study of vortex breakdown by particle tracking velocimetry (PTV), part 3: time-dependent structure and development of breakdown modes. Exp. Fluids 18, 174–186.Google Scholar
Courant, R. & Hilbert, D. 1953 Methods of Mathematical Physics, vol. 1. Interscience.Google Scholar
Crane, C. M. & Burley, D. M. 1976 Numerical studies of laminar flow in ducts and pipes. J. Comput. Appl. Maths 2, 95–111.CrossRefGoogle Scholar
Darmofal, D. L. 1996 Comparisons of experimental and numerical results for axisymmetric vortex breakdown in pipes. Comput. Fluids 25, 353–371.Google Scholar
Dennis, D. J. C., Seraudie, C. & Poole, R. J. 2014 Controlling vortex breakdown in swirling pipe flows: experiments and simulations. Phys. Fluids 26 (5), 053602.CrossRefGoogle Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20, 1385–1400.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2004 The role of boundary conditions in a simple model of incipient vortex breakdown. Phys. Fluids 16 (2), 274–286.CrossRefGoogle Scholar
Gallaire, F., Chomaz, J.-M. & Huerre, P. 2004 Closed-loop control of vortex breakdown: a model study. J. Fluid Mech. 511, 67–93.Google Scholar
Garg, A. K. & Leibovich, S. 1979 Spectral characteristics of vortex breakdown flow field. Phys. Fluids 22, 2053–2064.Google Scholar
Granata, J.2014 An active flow control theory of the vortex breakdown process. PhD dissertation, Rensselaer Polytechnic Institute.Google Scholar
Grimshaw, R. & Yi, Z. 1993 Resonant generation of finite-amplitude waves by the flow of a uniformly rotating fluid past an obstacle. Mathematika 40, 30–50.Google Scholar
Hanazaki, H. 1996 On the wave excitation and the formation of recirculation eddies in an axisymmetric flow of uniformly rotating fluids. J. Fluid Mech. 322, 165–200.Google Scholar
Hoffman, K. A. & Chiang, S. T. 1993 Computational Fluid Dynamics for Engineers. Engineering Education System.Google Scholar
Howard, L. N. & Gupta, A. S. 1962 On the hydrodynamics and hydromagnetic stability of swirling flows. J. Fluid Mech. 14, 463–476.CrossRefGoogle Scholar
Ioos, G. & Joseph, D. D. 1989 Elementary Stability and Bifurcation Theory. Springer.Google Scholar
Kelvin, L. 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Lavan, A., Nielsen, H. & Fejer, A. A. 1969 Separation and flow reversal in swirling flows in circular ducts. Phys. Fluids 12, 1747–1757.Google Scholar
Leclaire, B. & Jacquin, L. 2012 On the generation of swirling jets: high-Reynolds-number rotating flow in a pipe with a final contraction. J. Fluid Mech. 692, 78–111.CrossRefGoogle Scholar
Leclaire, B. & Sipp, D. 2010 A sensitivity study of vortex breakdown onset to upstream boundary conditions. J. Fluid Mech. 645, 81–119.Google Scholar
Leclaire, B., Sipp, D. & Jacquin, L. 2007 Near-critical swirling flow in a contracting duct: the case of plug axial flow with solid-body rotation. Phys. Fluids 19 (9), 091701.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown: survey and extension. AIAA J. 22, 1192–1206.Google Scholar
Leibovich, S. & Kribus, A. 1990 Large amplitude wavetrains and solitary waves in vortices. J. Fluid Mech. 216, 459–504.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Lieb, E. H. & Loss, M. 1997 Analysis, CRM Proceedings and Lecture Notes, vol. 14. American Mathematical Society.Google Scholar
Long, R. R. 1953 Steady motion around a symmetrical obstacle moving along the axis of a rotating liquid. J. Met. 10, 197–203.Google Scholar
Lopez, J. M. 1994 On the bifurcation structure of axisymmetric vortex breakdown in a constricted pipe. Phys. Fluids 6, 3683–3693.Google Scholar
Mattner, T. W., Joubert, P. N. & Chong, M. S. 2002 Vortical flow. Part 1. Flow through a constant diameter pipe. J. Fluid Mech. 463, 259–291.Google Scholar
Meliga, P. & Gallaire, F. 2011 Control of axisymmetric vortex breakdown in a constricted pipe: nonlinear steady states and weakly nonlinear asymptotic expansions. Phys. Fluids 23, 084102.Google Scholar
Randall, J. D. & Leibovich, S. 1973 The critical state: a trapped wave model of vortex breakdown. J. Fluid Mech. 53, 48–493.Google Scholar
Rayleigh, L. 1916 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
Rusak, Z. 1998 The interaction of near-critical swirling flows in a pipe with inlet vorticity perturbations. Phys. Fluids 10 (7), 1672–1684.Google Scholar
Rusak, Z. & Judd, K. P. 2001 The stability of non-columnar swirling flows in diverging streamtubes. Phys. Fluids 13 (10), 2835–2844.Google Scholar
Rusak, Z. & Lamb, D. 1999 Prediction of vortex breakdown in leading-edge vortices above slender delta wings. J. Aircraft 36 (4), 659–667.Google Scholar
Rusak, Z. & Meder, C. 2004 Near-critical swirling flow in a slightly contracting pipe. AIAA J. 42 (11), 2284–2293.Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of near-critical swirling flows in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.CrossRefGoogle Scholar
Rusak, Z., Whiting, C. H. & Wang, S. 1998 Axisymmetric breakdown of a $Q$ -vortex in a pipe. AIAA J. 36 (10), 1848–1853.Google Scholar
Sarpkaya, T. 1971 On stationary and traveling vortex breakdowns. J. Fluid Mech. 45, 545–559.Google Scholar
Sarpkaya, T. 1974 Effect of adverse pressure-gradient on vortex breakdown. AIAA J. 12 (5), 602–607.Google Scholar
Sarpkaya, T. 1995 Turbulent vortex breakdown. Phys. Fluids 7 (10), 2301–2303.Google Scholar
Silvester, D. J., Thatcher, R. W. & Duthie, J. C. 1984 The specification and numerical solution of a benchmark swirling laminar flow problem. Comput. Fluids 12, 281–292.Google Scholar
Snyder, D. O. & Spall, R. E. 2000 Numerical simulation of bubble-type vortex breakdown within a tube-and-vane apparatus. Phys. Fluids 12 (3), 603–608.CrossRefGoogle Scholar
Squire, H. B. 1960 Analysis of the vortex breakdown phenomenon. In Miszallaneen der Angewandten Mechanik, pp. 306–312. Akademie.Google Scholar
Struwe, M. 2008 Variational Methods, Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems. Springer.Google Scholar
Synge, L. 1933 The stability of heterogeneous liquids. Trans. R. Soc. Can. 27, 1–18.Google Scholar
Umeh, C. O. U., Rusak, Z., Gutmark, E., Villalva, R. & Cha, D. J. 2010 Experimental and computational study of nonreacting vortex breakdown in a swirl-stabilized combustor. AIAA J. 48 (11), 2576–2585.Google Scholar
Wang, S. 2009 On the nonlinear stability of inviscid axisymmetric swirling flows in a pipe of finite length. Phys. Fluids 21, 084104.Google Scholar
Wang, S. & Rusak, Z. 1996a On the stability of an axisymmetric rotating flow in a pipe. Phys. Fluids 8 (4), 1007–1016.Google Scholar
Wang, S. & Rusak, Z. 1996b On the stability of non-columnar swirling flows. Phys. Fluids 8 (4), 1017–1023.Google Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar
Wang, S. & Rusak, Z. 2011 Energy transfer mechanism of the instability of an axisymmetric swirling flow in a finite-length pipe. J. Fluid Mech. 679, 505–543.Google Scholar
Xu, L.2012 Vortex flow stability, dynamics and feedback stabilization. PhD dissertation, Rensselaer Polytechnic Institute.Google Scholar